ヨッシンと 地学の散歩
散歩道の四方山話
散歩道の四方山話
地球は丸いといわれていますが、実際に地面を眺めてみても丸いと感じることはありません。 球形なら地平線付近の地面が向こうに下っていくように見えるはずですが、そのようには見えません。 そのため古代の人たちの考える地球は平らなものがほとんどです。地の果てはどうなっているとか、 地球はどのように支えられているかといった点で多少の変化が見られます。それでも根本は平らな地球を考えています。
地球が平らに見えるのは、私たちが見ることができる範囲に比べて、地球が非常に大きいからです。そのため、 遠くの地平線付近の向こう側への落ち込みは非常に小さく、ほとんど水平と感じ、地球の表面の形としてとらえるためです。 飛行機のような上空から見ても、地上とそれほど違いは感じられないでしょう。
地球が丸い証拠をという質問に対して、「水平線が丸いから」という答えは適切ではありません。円盤形の地球でもそのように見えるからです。 平面図形の円と立体図形の球との混同が見られます。地球が丸い、正確なことばでは球形であるということを考えてみます。
ここに証拠のようにあげられたものは、実際に確認できるものもありますし、たんに理論上こうなるはずだというものもあります。 確かにこうなっているから、地球が球形だと考えるのが大事だと思います。
1.遠くのものの見え方
1 遠くから来る船は帆先から見える
2 遠方では違う世界が広がっている
3 高いものほど遠くにあっても見える
4 高いところほど遠くが見える
5 どれだけ遠くがみえるか
6 考え方の問題点
2.星の見える高さが違う
1 北極星の高度は緯度に等しい
2 南に行くと見えなかった星座が見えてくる
3 北極圏地方での太陽の動き
4 太陽の高度から地球の半径が求められる
5 東西に移動すれば時差が生じる
3.その他の証拠
1 月食の時の地球の影の形
2 富士山と日の出
2'夕陽に照らされる雲
3 平面と球面上の幾何学
4 東に行けば元に戻ってくる
5 宇宙から見た地球の姿
4.地球が丸いと起こる不思議
1 遠方の地面は落ち込んでいない
2 地球の裏側の人は落ちてしまう
3 万有引力の証明
5.地球はなぜ丸いのか
1 遠くから来る船は帆先から見える
2 遠方では違う世界が広がっている
3 高いものほど遠くにあっても見える
4 高いところほど遠くが見える
5 どれだけ遠くがみえるか
6 考え方の問題点
2.星の見える高さが違う
1 北極星の高度は緯度に等しい
2 南に行くと見えなかった星座が見えてくる
3 北極圏地方での太陽の動き
4 太陽の高度から地球の半径が求められる
5 東西に移動すれば時差が生じる
3.その他の証拠
1 月食の時の地球の影の形
2 富士山と日の出
2'夕陽に照らされる雲
3 平面と球面上の幾何学
4 東に行けば元に戻ってくる
5 宇宙から見た地球の姿
4.地球が丸いと起こる不思議
1 遠方の地面は落ち込んでいない
2 地球の裏側の人は落ちてしまう
3 万有引力の証明
5.地球はなぜ丸いのか
1.遠くのものの見え方
地球が丸い場合と平らな場合で遠くのものの見え方が変わってきます。最初に地球が球形だと証拠を挙げていったのは、 アリストテレスとされています。簡単な幾何学を応用することで、地球の形によって遠くのものの見え方が変わってくる事がわかります。
1-1 遠くから来る船は帆先から見える
アリストテレスが地球は球形である証拠としてあげたものの中の代表的なものです。実際には、 これが最大の論拠となっているといっていいでしょう。
帆先から見えるというのは、具体的にどのように見えるのでしょうか。帆が最初に空中に現れ、 次第に船体の低い部分が浮かび上がってくるというものではありません。地球が球形だとすると、遠くにいる船は水平線下に沈んでいて、 次第に水平線上に浮かんで上がってくる様に見えます。
もし地球が平らだとすると、観察者からは地球の果てまで見えます。遠くの船は、小さく見えるだけで、そのほかの見え方は全く同じです。
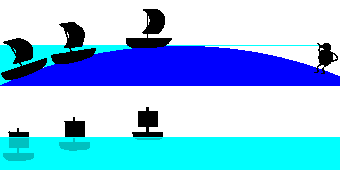 これに対して、球形だとすると、地平線より遠くの船の見え方が変わってきます(右図)。青丸が地球とします。
右側の観測者から見ると地球と空との境界線は、目から引いた地球への接線(水色線で記入)の方向になります。この線と地球との接点が、
水平線になります。図では左側、水平線の向こうから来る船は、水平線より下側にある地球の影になって見ることができません。
図の左端に記した船の位置では、穂先だけが、水平線上にわずかに顔を出しているように見えます(上段左端の図)。そう少し近づいた船では
(真ん中の船)、帆全体が水平線上にありますが、船体は水平線下でまだ見えていません。さらに近づくと(右端の船)では、
底部の一部を除いて全て見えるようになります。近づく船は、図上段の左側のものから順に変化していくように見えます。
これに対して、球形だとすると、地平線より遠くの船の見え方が変わってきます(右図)。青丸が地球とします。
右側の観測者から見ると地球と空との境界線は、目から引いた地球への接線(水色線で記入)の方向になります。この線と地球との接点が、
水平線になります。図では左側、水平線の向こうから来る船は、水平線より下側にある地球の影になって見ることができません。
図の左端に記した船の位置では、穂先だけが、水平線上にわずかに顔を出しているように見えます(上段左端の図)。そう少し近づいた船では
(真ん中の船)、帆全体が水平線上にありますが、船体は水平線下でまだ見えていません。さらに近づくと(右端の船)では、
底部の一部を除いて全て見えるようになります。近づく船は、図上段の左側のものから順に変化していくように見えます。
 実際に、遠方の船がどのように見えるか観察してみたことがあります。実際に上部の船室だけが水平線上に顔を出すくらいの距離にある船は、
非常に小さくどのようになっているか判断できません。視力のいい人なら見えるのかもわかりませんが、通常の視力では無理なようです。
それでも沖合をいく船が、やけに沈んでいるように見える程度のことは観察できます。
右の写真は、遠ざかっていくフェリー(左)や船()右を写したものです。フェリーの写真一番上では、全体が写っていますが、
2番目では車両甲板床面は海面下にあります。4番目のものは車両甲板天井あたりまで沈んでいるようですが、かすんでいてよくわかりません。
もちろんこの時には、肉眼では見えていません。船の写真でも、段々沈んでいくように見えるのがわかると思います。
一番下では甲板も沈んでしまっています。双眼鏡で見ていたのですが、いきなり船が消えたように見えました。
実際に、遠方の船がどのように見えるか観察してみたことがあります。実際に上部の船室だけが水平線上に顔を出すくらいの距離にある船は、
非常に小さくどのようになっているか判断できません。視力のいい人なら見えるのかもわかりませんが、通常の視力では無理なようです。
それでも沖合をいく船が、やけに沈んでいるように見える程度のことは観察できます。
右の写真は、遠ざかっていくフェリー(左)や船()右を写したものです。フェリーの写真一番上では、全体が写っていますが、
2番目では車両甲板床面は海面下にあります。4番目のものは車両甲板天井あたりまで沈んでいるようですが、かすんでいてよくわかりません。
もちろんこの時には、肉眼では見えていません。船の写真でも、段々沈んでいくように見えるのがわかると思います。
一番下では甲板も沈んでしまっています。双眼鏡で見ていたのですが、いきなり船が消えたように見えました。このようなことを確認できないとしても、見方を変えることで地球が丸いことの証拠を挙げることができます。
1-2 遠方では違う世界が広がっている
地球が平たい場合と、丸い場合の違いは、地の果てが地平線かそれまでの途中の地点が地平線になる点です。 平たい場合は遠くに見える小さな景色がだんだん大きくなって見えるのに対して、丸い場合は進んでいくに従って地平線は向こう側に移動し、 新たな世界が見えてくることになります。大阪からは名古屋の風景は見られないし、名古屋に行っても東京の景色を見ることができません。
1-3 高いものほど遠くにあっても見える
遠方にある船の帆先が見えるのは、帆先が高いところになるからです。遠くの船の帆先だけがみえる事を簡単に言えば、高いところにある帆先は、 低いところにある船体より遠くにあっても見ることができるということになります。
船ではなく、山で考えてみましょう。2〜30m程度の小高い丘では数km離れたところではすでに見えなくなっています。 山の高さが500mにもなると隣接している平野のどこからでも見ることができるようになります。。 このように山が高くなればなるほど遠くから見えるようになるのは地球が丸いからだといえます。 実際に、富士山がどれだけ離れた所から見えるかということが調べられています。その記録は、奈良県の大峰山系で400km近く離れています。 奈良県・三重県の県境の大台ヶ原山にはここから富士山が見えますという標識がありますし、京都府・ 滋賀県の比叡山や比良山から富士山を見たことがあります。
1-4 高いところほど遠くが見える
先ほどのことを逆に考えてみましょう。富士山に登れば、西は大峰山系や比良比叡山系まで見えることになります。 ふつうの山ではこれほど遠くを見ることはできません。これも、富士山が高く、地球が丸いからに他なりません。
富士山ほど高い山でなくても、見晴らしがよくなるのは遠くまで見えるようになっているからです。高い山や塔、 ビルに展望台が作られたりするのは遠くが見えるようになるからです。火の見櫓が高いところに造られたり、 海賊船の帆先に物見台があったりするのは全て高いところほど遠くまで見渡せるからです。 同様に東京タワーやスカイツリーといった電波塔が高いのも同じ理由です。
 右の写真は、鳥取砂丘の海岸から沖合にある島(海士島)を写したものです。左側は波打ち際で座って、真ん中は波打ち際で立って、
右側は砂丘の上から撮りました。左の写真では、水平線がほぼ島の位置に一致しています。真ん中の写真では、水平線は島のわずかに遠方にあり、
島の岩礁部より上に水平線が見えています。右の写真では島の向こう側に広く水平線が広がっています。この3枚の写真から、
高いところほど遠くが見えることがわかります。
右の写真は、鳥取砂丘の海岸から沖合にある島(海士島)を写したものです。左側は波打ち際で座って、真ん中は波打ち際で立って、
右側は砂丘の上から撮りました。左の写真では、水平線がほぼ島の位置に一致しています。真ん中の写真では、水平線は島のわずかに遠方にあり、
島の岩礁部より上に水平線が見えています。右の写真では島の向こう側に広く水平線が広がっています。この3枚の写真から、
高いところほど遠くが見えることがわかります。1-5 どれだけ遠くがみえるか
高く上がればどれだけ遠くが見えるかを計算してみることにします。いちばん遠くの地点は地平線(水平線)となります。ここで、地平線上の一点、 山の山頂、地球の中心の3点が作る三角形を考えてみることにします。地平線上の一点は地球への接線ですから、この三角形は、 地平線のある角が90度の直角三角形になります。このことからピタゴラスの定理(三平方の定理)を使って次の式を作ることができます。
地球の中心から山頂までの距離の2乗=地球の半径の2乗+地平線までの距離の2乗
ここで、地球の中心から山頂までの距離は地球の半径+山の高さです。言葉がが長くなりますので記号で表すことにします。 地平線までの距離をd、地球の半径をR、山の高さをhとすると、
(R+h)2=R2+d2
R2+2Rh+h2=R2+d2
d2=2Rh+h2
d2=2Rh(1+h/2R)
ここでh/Rは最大(一番高い山)でも700分の1しかありませんので、無視できるとして
d2=2Rh
d=(2Rh)0.5=(2R)0.5×h0.5 0.5乗は平方根のことです
R=6400000mを代入して
d=(12800000×h)×0.5
=(2560000×5×h)0.5
=((1600)2×5×h)0.5
=1600×50.5×h0.5
=3600×h0.5
山の高さの平方根の3600倍の距離まで見えることになります。たかさが1m(子どもの目の高さ)だと3.6kmまで、1.5mだと4.4km、 20mのビルの屋上だと16km、富士山頂だと220kmになります。富士山がどれだけ遠くから見えるかという記録がこれより長いのは、 見る山の高さも関係してくるからです。
1-6 考え方の問題点
これからの話にも関係してきますが、ここまでの話で大きな仮定が一つ入っています。それは、光線がまっすぐ進むということです。 もし、光が上の方に曲がるのなら、地球が平らでも地球が丸い場合と同じように見えるはずです。実際には沈む星の動きから、 光は下の方に曲がるのがわかっています。これは大気差と呼ばれ、地球の大気の濃度が地平線近くほど濃くなり、 その影響で光の速度が遅くなり屈折して起こります。地表付近の温度の状態によっては、上の方に曲がることがありますが、 よく起こっている現象ではなく、これが起こればすぐにわかります(逃げ水など)ので、影響を除外することができます。 実際には光はまっすぐ進んでいると考えていいでしょう。
もう一つ注意して欲しいことは、これらの方法で証明される事柄のほとんどが、「真ん中が膨らんだ形」であるということです。 完全な球形なのか、卵形なのか、ラグビーボール型、まんじゅう型、UFO型といった形どれにでも当てはまることです。 球形であるという事を証明しようとすると地球全体からまんべんなく数カ所膨らみ具合を測定し、全て同じであることを求める必要があります。 次章に出てくる「4太陽の高度から地球の半径が求められる」類似の方法を使って地球の形が求められた結果、地球の形は完全な球形ではなく、 赤道方向にほんのわずかだけ膨らんだ形であることがわかっています。
2.星の見える高さが違う
観察できる遠くのものを、さらに遠くして星の世界にまで遠方にしたらどうなるのかを考えてみます。 遠くから来る船の場合の応用型と見ることもできますが、感じが変わるので別項として扱うことにします。
2-1 北極星の高度は緯度に等しい
北に行くほど北天の星座の高度は高くなっていきます。地球が丸くても平らでもこの現象は起こります。違うのは、 地球が平らな場合は星座の高度が上がっていくに従ってわずかな移動で高度が大きく変化するのに対して、地球が丸い場合は星座の高度に関係なく、 高さの変化は移動距離に比例する点です。実際に見えるのは後者ですが確認するのは、難しいことです。 星座の変化は100kmの移動で約1度になりますので、高度が変化したと実感できるまでは相当な距離を移動しなければならないことがわかります。
星座は日周運動で高度が変化しますので、動かない北極星を使って観測するのがいちばんやりやすい方法です。 それでも北極星は約1度の半径で回転していますので、その影響を除去するためには相当な距離を移動しなければいけません。
北極星が動かない位置(天の北極)にいるとしたとき、理論上は高度は緯度に等しくなります。このことを逆に利用して、 北極星の高度から緯度を求めることができ、このようにして求めた緯度を天文緯度といいます。実際に天文緯度を求めようとすると、 天の北極には目印になる星がないため、正確に求めるのに苦労します。代わりに頭の真上(天頂)を通る恒星の座標(赤緯=天文緯度) を利用することで天文緯度を求めています。
 天の北極の高度が高くなっていくに従って、北極星の下側を通る星が増えていきます。これらの星は、地平線下に沈むことがなく、
周極星と呼ばれています。近畿地方では北斗七星は地平線下に少しだけ沈みます(正確には2星が沈み5星は地平線ぎりぎりを通ります)が、
北海道にまで北上すると沈まなくなります。周極星の数は、北に行くほど増えていきます。
右写真は稚内で撮影したものです。北極星の高度が高く、カシオペア座の星々が周極星になっています。
天の北極の高度が高くなっていくに従って、北極星の下側を通る星が増えていきます。これらの星は、地平線下に沈むことがなく、
周極星と呼ばれています。近畿地方では北斗七星は地平線下に少しだけ沈みます(正確には2星が沈み5星は地平線ぎりぎりを通ります)が、
北海道にまで北上すると沈まなくなります。周極星の数は、北に行くほど増えていきます。
右写真は稚内で撮影したものです。北極星の高度が高く、カシオペア座の星々が周極星になっています。2-2 南に行くと見えなかった星座が見えてくる
北に行ったばあい、北極星の高度が上がるのなら、南側の星座は低くなります。地球が平たい場合は、星座が圧縮されていくように見えるますが、 丸い場合は低いものから順番に地平線下に沈んでいきます。北に行くと南の星座がだんだん見えなくなっていきます。

 南に進んでいくと逆に、南天にあるの星座が見えるようになります。南国の星として有名な南十字星は本州からは見ることのできませんが、
沖縄では南の地平線上に見ることができます。実際には、天候など加減で見るのは非常に難しいようです。
南に進んでいくと逆に、南天にあるの星座が見えるようになります。南国の星として有名な南十字星は本州からは見ることのできませんが、
沖縄では南の地平線上に見ることができます。実際には、天候など加減で見るのは非常に難しいようです。右に小笠原母島(左側)と稚内(右側)での写真を並べています。両方に台形に並んだからす座が写っていますので比べてみてください (母島では右上、稚内では中断左寄りに写っています)。 母島の写真には、ケンタウルスαβや南十字βγ(右下部に拡大)といった本州では見ることができない星が写っています。
 南天の1等星で、カノープスという星があります(右写真)。近畿地方からは計算上では南の地平線ぎりぎりのところに見えるはずです。
あまりにぎりぎりなので、光が通り抜ける大気の層があつくなり、減光されて見えにくくなります。おまけに地平線上に出ている時間も短くなります。
めったに見られないことから、この星を見ると3年長生きするとかいう伝説さえ生まれています。これが、南の沖縄に行くと高度も相当高くなり、
出ている時間も長くなるのでかなり見つけやすくなります。逆に北に行くとさらに見つけづらくなり、上って来なくなるところが現れます。
どれまで北の地点で見つけられるかということも調べられており、現在の所福島県あたりが最北のようです。
予想されるより北の地点で、見つけられているのは、先ほど説明した大気差が原因とされています。
南天の1等星で、カノープスという星があります(右写真)。近畿地方からは計算上では南の地平線ぎりぎりのところに見えるはずです。
あまりにぎりぎりなので、光が通り抜ける大気の層があつくなり、減光されて見えにくくなります。おまけに地平線上に出ている時間も短くなります。
めったに見られないことから、この星を見ると3年長生きするとかいう伝説さえ生まれています。これが、南の沖縄に行くと高度も相当高くなり、
出ている時間も長くなるのでかなり見つけやすくなります。逆に北に行くとさらに見つけづらくなり、上って来なくなるところが現れます。
どれまで北の地点で見つけられるかということも調べられており、現在の所福島県あたりが最北のようです。
予想されるより北の地点で、見つけられているのは、先ほど説明した大気差が原因とされています。2-3 北極圏地方での太陽の動き
星が見えたり見えなかったりするのなら、太陽だって同じはずです。南に行けば太陽の南中高度は上がり、北に行くほど下がっていきます。 冬の太陽が低くしか上がらない時期に北の地域に行けば、そのうち太陽が全く昇ってこない地域にたどり着きます。 太陽が全く昇らない、一日中夜の状態を極夜といいます。このように極端ではなくても、冬の北国は昼間が非常に短く感じられます。 逆に夏になると、昼間の長さが長くなります。太陽が北よりの場所から昇り、北よりの場所に沈んでいきます。 さらに北に進んでいくと、太陽の沈む位置がだんだん北により、沈んでいる時間もだんだん短くなっていきます。 最終的には、太陽は周極星のように全く沈まなくなります。太陽が沈まないか、 沈んでも空が暗くならないうちに再び太陽が昇ってくるような夜のことを白夜といいます。一般的には「びゃくや」と読むことが多いようです。 極夜や白夜になるような地域は北極圏(南半球では南極圏)といい、緯度が66.6度(90度から地軸の傾きを引いた値)より大きな地域になります。
地球上に太陽が沈まない地域、全く昇ってこない地域があるのも地球が丸い証拠となります。
2-4 太陽の高度から地球の半径が求められる
太陽の高度が場所によって変わる事が、地球が丸いためだと仮定すると、地球の半径を求めることができます。 太陽の高度差は2地点の地球の中心に対する中心角になります。中心角の大きさと弧の長さは比例します。 このばあいの弧の長さは2地点間の距離ですから、中心角が1周の大きさになるときの弧の長さを求めます。 一周した弧の長さは全周の長さになりますから、これで地球の大きさが求められたことになります。
最初に地球の大きさを求めたのは、紀元前3世紀頃のエラトステネスとされています。 このあたりのいきさつについては教科書などに書かれているので、簡単に概略のみを書くことにします。 彼はまず、ナイル川河口のアレキサンドリアとナイル川をさかのぼったシエネでの太陽高度に違いがあり、 その大きさは1周の50分の1であると測定しました。2地点間の距離は、旅行の行程から50000スタジア(約900km)と求め、 地球全周の長さは250000スタジア(45000km)と求めました。
この測定結果は当時としては非常によい精度で求められていると評価されています。地球1周の長さ40000kmに比べ12.5%も大きい事が、 精度がいいといえるのか考えてみます。2地点の太陽高度の差は比較的精度よく求められています。2地点間の距離についてはどうでしょうか。 どうしても大きく求められる要素が含まれており、排除するのが困難だったと考えることができます。 2地点間の道のりは、直線距離に比べどれだけ長くなっているのかは知る方法がありません。また、現在の地図で見比べればわかりますが、 2地点は正確に南北の位置関係にあるわけではありません。これらの要素を考えてみると、 10〜15%程度大きな値が求められたところで当然の結果と考えていいでしょう。正確に求めようとなると、 2地点間を正確に測量していけばできたはずですが、地球の大きさを求めるためにだけに膨大な費用と年月を使ってまで求めると (後年やりましたが)いうのはちょっと考えられることではなかったでしょう。
最初に断っていたのですが、これはあくまでも地球は丸いと仮定した場合の話で、平らな場合でも同じように求めることができます。 その結果求められるのは太陽までの距離になります。もちろん、さらに南北に地域を広げ、 何地点かを利用し大きさの変化の様子を見れば地球が丸いのか平らなのかは決着をつけることができます。
2-5 東西に移動すれば時差が生じる
太陽が真南にあるとします。ちょうど正午の時刻となります。太陽は東から昇って西に沈むのですから、 東側にある場所では、その時刻より早く太陽が真南に来ます。正午になるのが早くなっています。西側の場所ではこれと逆のことが起こります。 時刻は太陽の角度(時角)から求められますので、東西に移動すれば時刻が違うことが起こります。一般的には時差と呼ばれている現象です。
時差があるのは、海外のスポーツ中継などを見ているときとか、海外旅行をしたときなどに感じることがあります。 現在では同じ瞬間である事を知る方法はいくらでもあります。例えば、時計などはその代表的な例です。そのような便利な器具がなかったとしたら、 同じ瞬間である事をどのようにして知ればいいのでしょうか。太陽の動きを使って時刻を知る方法は使えません。 太陽から求めた時刻(視太陽時といいます)が同じ瞬間でも場所によって異なっていることを求めたいからです。 この問題に懸賞がつけられたこともあったようです。決着が付いたのは正確な時計が発明された事によりますが、 ガリレオは木星とその衛星の運動を観測し互いに隠されたり前方を横切ったりという瞬間を利用する方法を提案したといわれています。
地球が平らな場合でも時差は生じます。それでも明らかに丸い場合に比べ起こり方に違いが見られます。 平らな場合は、日の出、日の入りの瞬間は、地球上のどの地点でも変わりません。そのため、 場所によって午前と午後の時間の長さが違うことになります。丸い場合はどこにいても同じ長さになります。 また、場所によって日が昇っていたり(昼)、いなかったり(夜)することがあります。 日本が昼間なのにアメリカが夜であったりするのは地球が丸いからだといえます。
3.その他の証拠
高いところのもの、星の見え方あるいはそれの派生させたものから地球が丸い事の証拠といえるものをあげてきましたが、 それ以外のものを見ていくことにします。
3-1 月食の時の地球の影の形
アリストテレスは、月食の時に月面に落ちる地球の影の形が円形であることも、地球が丸い証拠としてあげています。 当時としては、月食がどのようにして起こるのかということから、正しく説明するのはかなりの知識が必要でした。 月食の原因として考えられていたのは、夜空に魔物が住んでいて、それが月を食べるのだといったものもあったようです。
 月食の時の地球の影といっても、まん丸の地球の形が影になっているわけではありません。地球の影の直径の方が、月の大きさより大きいので、
影の輪郭線が円弧の一部であるに過ぎません。実際に観察してみて影の輪郭線が円形かどうかは判断しづらいところもあります。
月が小さいのもありますが、月面上に地球の本影があたっていたとしても半影の幅は、月の直径と同じ大きさがあります。
その間は、徐々に明るさが変化していくことになります。月の表面には、明るい陸と暗い海があります。そのため、
海の部分では影が大きくなっているように見えます。なんとなく、影の輪郭線が不規則に曲がっているようにも見えます。
円弧の一部と判断しづらい所もあります。
月食の時の地球の影といっても、まん丸の地球の形が影になっているわけではありません。地球の影の直径の方が、月の大きさより大きいので、
影の輪郭線が円弧の一部であるに過ぎません。実際に観察してみて影の輪郭線が円形かどうかは判断しづらいところもあります。
月が小さいのもありますが、月面上に地球の本影があたっていたとしても半影の幅は、月の直径と同じ大きさがあります。
その間は、徐々に明るさが変化していくことになります。月の表面には、明るい陸と暗い海があります。そのため、
海の部分では影が大きくなっているように見えます。なんとなく、影の輪郭線が不規則に曲がっているようにも見えます。
円弧の一部と判断しづらい所もあります。影の輪郭線が円弧の一部をなしているとして、地球が球形だというためには、明け方か夕方に起こる日食で地球の影の形を確認する必要があります。 真夜中の月食では、円板型の地球でも丸い影を月に落とすことができます。また完全な形を知りたいのなら、月が地球の影の中心を通るとき、 北側を通るとき、南側を通るときと何回も観測する必要があります。
3-2 富士山と日の出
地球の影で地球の形がどのようになっているかを考えられないか検討してみます。高い山に朝の光が当たり始める様子を見てみます。 考えやすくするために、独立峰である富士山を例にすることにします。
 富士山に登る人のほとんどは、御来光を拝みにいくことが目的のようです。右写真は、富士山頂(三角点)からの御来光のようすです。
御来光が現れる瞬間は、富士山頂から見ると地平線の延長に太陽が重なって見えるときです。
さらに時間がたっていくと次第に低いところに日が当たるようになり、最後にはふもとにまで当たるようになります。
ここで、国立天文台の日の出時間を計算させるページで、富士山頂と同地点での標高0mの場所の2月28日の日の出時間を求めてみました。
その結果は山頂で6時7分、標高0mで17分と10分の差がありました。
2月28日の日の出はこのように観測されるものとして考えることにします。
太陽の昇った高さは、斜め55度の角度で昇っていくことを考慮して約8分ぶんになります。
太陽の動きは4分で1度ですから、この時間の間に角度で2度昇っていきます。
富士山に登る人のほとんどは、御来光を拝みにいくことが目的のようです。右写真は、富士山頂(三角点)からの御来光のようすです。
御来光が現れる瞬間は、富士山頂から見ると地平線の延長に太陽が重なって見えるときです。
さらに時間がたっていくと次第に低いところに日が当たるようになり、最後にはふもとにまで当たるようになります。
ここで、国立天文台の日の出時間を計算させるページで、富士山頂と同地点での標高0mの場所の2月28日の日の出時間を求めてみました。
その結果は山頂で6時7分、標高0mで17分と10分の差がありました。
2月28日の日の出はこのように観測されるものとして考えることにします。
太陽の昇った高さは、斜め55度の角度で昇っていくことを考慮して約8分ぶんになります。
太陽の動きは4分で1度ですから、この時間の間に角度で2度昇っていきます。地平線までの距離 日の出の時間差からわかるのは、富士山頂から見ると太陽高度が水平より2度低いときに日の出になり、 太陽の方向に地平線(地の果て)があることになります。このことを使って地平線までの距離を概算してみることにします。 図で富士山頂(藤色三角形)から見た右下がりの赤線は水平より2度下に向かっている線とします。この線上に地平線があります。 わかりやすくするため図の角度は10倍にしてあります。
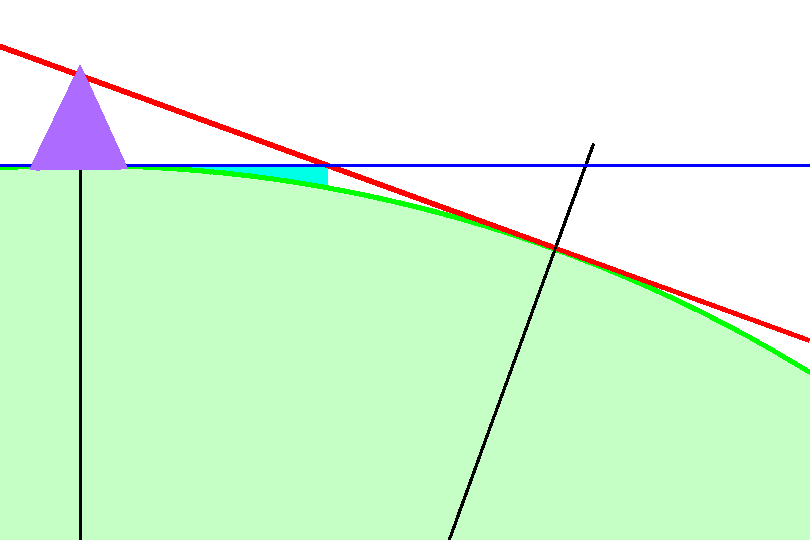 地球が球形の場合、地平線上の点(この斜め線と地球の接点)と富士山との地球の中心に対する中心角は太陽高度が低くなっている角度と同じで、
2度です。三角比の関係を使うと地球の中心から富士山頂までの長さと地球の半径の比は、中心角2度に対する余弦(コサイン)ですから、
地球の半径をR、富士山の高さを3.8kmとして、
地球が球形の場合、地平線上の点(この斜め線と地球の接点)と富士山との地球の中心に対する中心角は太陽高度が低くなっている角度と同じで、
2度です。三角比の関係を使うと地球の中心から富士山頂までの長さと地球の半径の比は、中心角2度に対する余弦(コサイン)ですから、
地球の半径をR、富士山の高さを3.8kmとして、(R+h)cos 2°=3.8 km
R = 3.8÷(1− cos 2°) ≒ 6240km
地平線までの距離はこれの角度2°に対する正接(タンジェント)をもとめればいいので
R × tan 2°≒ 220km
この値は、この距離は「どれだけ遠くが見えるのか」で計算して求めた地平線までの距離の計算結果と一致しています。 単に同じ計算を方法を変えてやっただけに過ぎませんから当然の結果です。違いは、地球の半径がわかっているものを使ったか、 現象から求めてやったかという点のみです。
次に、地球が平らだとして地平線までの距離を求めてみます。図で、水色の細長い長方形が平らな地球になります。 富士山までの高さと地平線までの距離の比は、山頂から見下ろす線の角度の正弦(サイン)になりますから、
地平線までの距離=3.8km ÷ sin 2°≒ 110km
と求めることができます。思ったより小さな地球となってしまいました。地平線までの距離を求めた時、 平らな場合は丸い場合の約半分になることを証明できます。
富士山から110kmといえば東は東京、西は浜松あたりで、220kmでは西は伊勢湾あたりになります。 山頂からどこまで見えるかは確認できていませんが浜名湖や東京から余裕で確認できることから、このあたりは十分見えているものと思われます。 したがって、富士山頂どこまで見えるかを考えても、平らな場合のはるか遠方まで見えることより、地球が丸い事を証明できます。
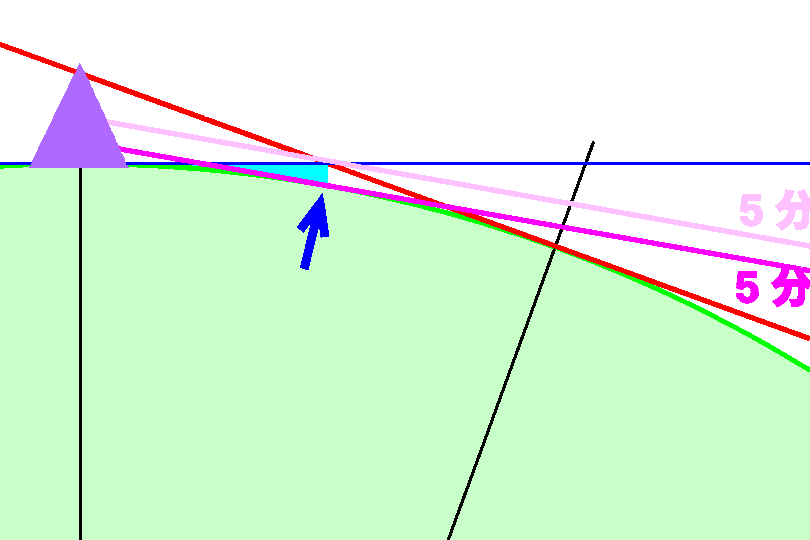 山腹への日の当たり方 山頂が日の出になってから、5分後を考えてみることにします。この時刻にはふもとでは、
まだ日の出になっていません。山の中腹より上側に陽が当たっているようすを見ることができます。この時の太陽高度は−1度です。
先ほどの図に紫線を追加して説明します。
山腹への日の当たり方 山頂が日の出になってから、5分後を考えてみることにします。この時刻にはふもとでは、
まだ日の出になっていません。山の中腹より上側に陽が当たっているようすを見ることができます。この時の太陽高度は−1度です。
先ほどの図に紫線を追加して説明します。地球が平らな場合、地平線のへりから、影の境界線が上ってきます(5分とかいた薄紫色線)。それに対して丸い場合は、 地球への接線になります(5分と書いた濃紫線)。二つの線の高さは明らかに違います。 丸い場合の方が早くふもとに日が当たるようになることがわかります。
こちらの方が高いとか低いといっても、もう一方がどの高さなのかわからないので、比べることができません。 そこで、角度と高さの関係を調べることにします。
地球が平らな場合、日が当たり始めているところの高さは、地平線までの距離×太陽高度の正接になります。 角度が1度や2度といった小さな角度では、正接の値は角度に比例すると考えるのが一般的です。従って、日があたり始めているところの高さは、 太陽高度に比例することになります。太陽高度は一定の速さで上がっていきますので、日の当たり始める高さは、 一定の速度で降りてくることになります。
補足:tan( θ ) = θ + θ3/3 + 2×θ5/15 + …… と表されます。
地球が丸いとどうでしょうか、「どれだけ遠くが見えるのか」の結果を利用して求めてみることにします。地平線までの距離は、 地球の中心角で表すこともできます。中心角に対する円弧の長さだからです。中心角をθとして、d=kθと書くことができます (θを弧度法で表せばkは地球の半径Rになります)。従って「どれだけ遠くが見えるのか」で求めた式に代入してから両辺を2乗して
(kθ)2=13h
このことから日の当たり始める高さは、太陽高度の2乗に比例することがわかります。
実際にどちらの現象が起こっているのでしょうか。富士山に陽が当たっていくようすを早送りで見たとします。 日の当たり始めている高さは、地球が平らだと一定の速度で降りてくるのに対して、丸いと始めは早くだんだん降りる速度がゆっくりになってきます。 山に日が当たり始めている早送り映像を見た限りでは、後者のようになっています。もちろん細工しているとは思えません。 (そこまで考えて作っているとは)。はっきりと確かめてみる必要はあります。今のところ確認はできていません。
−−−補足(2017.06.10)−−−−
太陽は点光源だとして計算しています。実際にはある程度の大きさ持って見えます。そのため影もある程度の幅を持ってきます。 電線が影が地面にできないはこのためです。この影響を考えてみることにします。
太陽の見える大きさは、距離と実際の大きさとの関係で表すことができます。直径が140万kmの太陽が1億5千万kmの所にあります。 これを比率で表すと、距離に対して、100分の1の大きさです。
従って、太陽の光がものに当たって影を作ったとして、その影の輪郭線は影までの距離の100分1の大きさだけぼやけるということになります。 ここで、富士山山頂で太陽の下端が出てきた瞬間を考えてみます。地球が丸い場合、地平線までの距離は220kmですから、 富士山にあたる影がぼやける大きさはその100分の1の2.2kmになります。 つまり、山頂の3800mより2200m低い1600mの山腹で、太陽の上端が昇ってくるいわゆる日の出となっています。 富士山の高さの半分以上の幅で影の線がぼやけるということになります。 これだけを単純に考えれば、うまくいかないのではというように思えてきます。
太陽の光が当たり始めた瞬間は急に明るくなります。日の出とともに周囲の景色が急に明るくなるのと同じです。 太陽が昇りきらなくてもかなり明るくなっています。光の全く当たっていないところと、あたっているところの区別は容易でしょう。 月食の時の地球の影の輪郭を見ればわかります。写真にとるとぼやけるものの境界線は何となくわかります。
影の輪郭のぼやけることを利用しても、地球の形のがどのようになっているかを知る手がかりが得られそうです。 もし地球が平たい場合、地平線までの距離は110kmでした。丸い場合の半分です。輪郭がぼやける大きさも半分の1.1kmになります。 この大きさははっきりとはわからないでしょう。逆に太陽がどのように見えているかを利用することで地球の形を知る手がかりとなるでしょう。 たとえば、山頂で太陽ができった瞬間に、日が昇り始めるのが1600mなのか2700mなのかを調べてみることにします。 1600mなら丸い地球、2700mなら平らな地球を示すことになります。
−−−補足2(2017.12.13)−−−−
2017年7月26日の夕刻に、御嶽山近辺に巨大な積乱雲ができました。 この時、中国・近畿・東海地方周辺にも目立った雲はなく、単独の大きな雲だったようです。 大阪からは200km離れているにもかかわらず、はっきりと見ることができました。 できていたのが日没直前だったので、山にあたる朝日の代わりに使えると考えました。 そこで、雲に日が当たらなくなるまでをインターバルで撮影しました。 写真をタイムラプス動画にしたものがこの動画です。7時10分頃から約10分間の映像です。
影の移動のようすははっきりしません。何となく、影がはっきりと見え始めるまでに時間がかかり、その後すぐに雲頂まで移動しているように見えます。 肝心な時間帯はカメラにトラブルがあってうまく写せていないのと、地面近くはもやがかかって影の様子がわかりにくい、 見えている雲の下端の高さは距離が遠いことが原因で3000mは越えていたと思われること、 自動露出にしていたために途中で明るさが変わっていたりといったことが影響しているようです。 もうちょっと近い距離、たとえば岐阜あたりからだったら何とかなったかも知れません。
−補足2に追加(2024.03.10)−
 2012年8月19日の日没時に東の空にできていた積乱雲を10秒インターバルで撮影していました。
これを一定幅で切り出し、左側から時間順に並べてみました。その結果が右写真になります。
2012年8月19日の日没時に東の空にできていた積乱雲を10秒インターバルで撮影していました。
これを一定幅で切り出し、左側から時間順に並べてみました。その結果が右写真になります。はっきりとどちらということは決めかねます。 左半分では順調に杞憂の影に入って行っているようですが、 真ん中付近でいったん暗くなった後右側ではさらに低いところに日が当たっているように見えます。 これは、雲が移動していて、真ん中では雲がないところにさしかかったのと、手前側にある雲の影が落ちていたことの影響でしょう。 雲の下半分がずっと薄暗いのも判定を難しくしているようです。
どちらかといえばこれも失敗例になります。17年の例も含めて何度か挑戦しています。意外とチャンスは少なく今のところうまく写せていません。
 日出直後の山頂からの景色 山腹への日の当たり方で示した図をもう一度見なおして見ることにします(右図)。
別なところで、地球が平らな場合と、丸い場合で決定的な違いが現れています。
山頂日出5分後のようすですが、地球が平らな場合地表には日が当たっていません。これに対して丸い場合は、
青矢印で示したところより遠方では陽が当たっています。この位置は、富士山から見た地平線より手前側にありますので、見ることができます。
山頂から見ると、三日月の明暗境界線のように、地表に陽の当たっているところと、あたってないところが見えることになります。
その位置は時間がたつにつれ、だんだん近づいてきて、真下に達したら、今度は反対側の地平線に向かって遠ざかっていきます。
平らな地球では、ある一瞬に一斉に日が当たり始めます。どちらが起こっているのでしょうか。
昔富士山に登ったときはそこまで考えていなかったので確認していません。一度見ておきたいものです。
御来光の映像が多数公開されているようですので、その中に、地表(雲も含めて)への陽のあたり方がわかるものがあるかも知れません。
日出直後の山頂からの景色 山腹への日の当たり方で示した図をもう一度見なおして見ることにします(右図)。
別なところで、地球が平らな場合と、丸い場合で決定的な違いが現れています。
山頂日出5分後のようすですが、地球が平らな場合地表には日が当たっていません。これに対して丸い場合は、
青矢印で示したところより遠方では陽が当たっています。この位置は、富士山から見た地平線より手前側にありますので、見ることができます。
山頂から見ると、三日月の明暗境界線のように、地表に陽の当たっているところと、あたってないところが見えることになります。
その位置は時間がたつにつれ、だんだん近づいてきて、真下に達したら、今度は反対側の地平線に向かって遠ざかっていきます。
平らな地球では、ある一瞬に一斉に日が当たり始めます。どちらが起こっているのでしょうか。
昔富士山に登ったときはそこまで考えていなかったので確認していません。一度見ておきたいものです。
御来光の映像が多数公開されているようですので、その中に、地表(雲も含めて)への陽のあたり方がわかるものがあるかも知れません。富士山を例に挙げたのは、独立峰で、標高差が大きいためです。富士山に似た1500〜2000m級の山でも確認はできるはずです。 日の出日の入り時に飛行機で飛んでいればこの線はよく見えるでしょう。向きによっては、影が追い抜いていくのが見えるかも知れません(国内の場合です)。
−−−補足(2017.06.10)−−−−
この場合も、太陽が大きさを持っていることで明暗境界線がぼやけるでしょう。その幅は地球半径の100分の1の64kmになります。 300m程度の高さの山からみた地平線の半径がこれくらいになります。 地球が平らな場合は、どこでみても太陽は同じ高さに見えますから、地面の明るさはそこでも同じということになります。
まだ。他にもいろいろな要素が関係しそうです。たとえば、太陽が低くなってくると、太陽光線は横から地面に当たるようになります。 これを上から見ていたとすると、地面の明るさは太陽が沈む前から暗くなっていきます。 この影響で、暗くなっているところと明るくなっているところの境界線の幅はもっと広くなるでしょう。 日の出後10分ぐらいすると周囲はだいぶ明るくなったと感じます。この明るさから日が当たらなくなる所までの幅を考えてみます。 明るくなったときの太陽の高さは、太陽の大きさの3倍くらいになります。 境界線の幅も3倍になりますから約190kmです。2800mの高さから見る地平線の半径がだいたいこれくらいになります。
もう一つ影響するものがあります。地面の明るさは大気からの散乱光を受けて明るくなります。その分、境界線の幅は広くなるかも知れません。 真っ暗になるまではかなりの時間がかかりますが、その分その間で、この影響を受けて明るさが変わる度合いはゆっくりしています。 ほとんどないと言っていいかもしれません。また、この影響は太陽の光が少なくなり地面が暗くなるほど大きくなります。 真っ暗になるまでと考えなければ、これは境界線の幅を小さくするように働きそうです。
いずれにしても、地球が平らな場合は、地表は一様に暗くなっていきます。 太陽側の端で日が当たって明るいのに、反対側の端で日が当たらなくて暗くなっているかを確認できれば、地球が丸い証拠といえるでしょう。
 −−−補足2(2017.12.15)−−−−
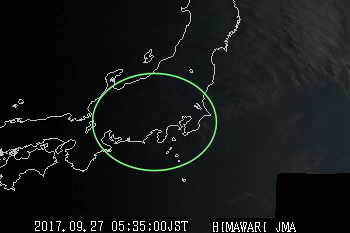
−−−補足2(2017.12.15)−−−−気象衛星ひまわりの画像を見ると、日の出時間に富士山からふもとを見た場合どのように見えるかということの見当をつけてみるることにします。
右図は、2017年9月27日午前5時35分のひまわりの可視画像です(気象庁のサイトからひまわり画像を引用)。 この時刻は、ふもとの三島付近では日の出時刻となっています。 参考のために、富士山を中心とした半径220kmの円のおおよその位置を緑色の楕円で示しています。これが富士山から見た地平線のおおよその位置となります。
円内を見ると、どこでもほとんど光が当たっていないように見えます。これは、どちらかというと露出不足が原因のようです。 日本列島東方沖海上の雲でさえほとんど明るくなっていません。 このあたりで日の出後2−30分は経過しているのでだいぶ明るく写ってもいいはずです。
犬吠埼付近は何となくですが、明るくなっているような感じがします。また、ここを中心にして見ると、東西で明るさが違うのがわかります。 もう10分もすれば、富士山付近でもこのあたりで見えている明るさになるはずです。これだと、明るさが違っているということが確認できるでしょう。
 朝日が当たる海面
普通海面上に朝日が昇ってくるときは、太陽の光が海面に反射して光って見えることがあります。
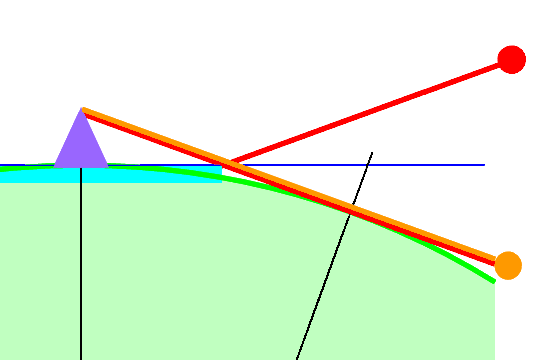
これが富士山のような高い山から見た場合、地球が丸いことの証明ができないか考えてみます(右図)。
地球の表面(海面)が凸凹のない滑らかな状態で、太陽の光を鏡のように反射するものとします。
日の出時の太陽の位置はオレンジ色の丸で示した位置とします。
朝日が当たる海面
普通海面上に朝日が昇ってくるときは、太陽の光が海面に反射して光って見えることがあります。
これが富士山のような高い山から見た場合、地球が丸いことの証明ができないか考えてみます(右図)。
地球の表面(海面)が凸凹のない滑らかな状態で、太陽の光を鏡のように反射するものとします。
日の出時の太陽の位置はオレンジ色の丸で示した位置とします。地球が平らな場合は、太陽の光が水平線で反射して、富士山頂に到着します。 水平線上から富士山頂をみあげる角度と、水平線上からみた太陽の高度は同じになります。 太陽の高度は地球上のどこで見ても同じです。富士山頂からみると、この高度まで太陽が昇ってくるまでは海面に太陽が反射して映って見えないことになります。 図で赤丸で示した位置です。光の経路は赤線で示しています。つまり、日の出から海面に太陽の光が反射し始めるまではしばらく時間がかかります。 日の出から地面に光が当たるまで8分。 そこから同じ角度だけ昇らないといけませんから、2倍の約16分間は海面に反射した太陽は見えない計算になります。
地球が丸い場合は、日の出の時の太陽(オレンジ色丸)からの経路は富士山頂を通る接線(オレンジ色線)になります。 この線は接点で左右対称ですから、太陽光が反射しているときの線(日の出太陽からの赤線)でもあります。 2つの線は重なっていますから、日の出と同時に海面で反射した光が見られることになります。
簡単に識別できそうな感じがします。御来光の写真は1枚載せています。これは雲の上から上がってきています。この証明には使えません。 ネットをみればたくさん見つけられます。他にないか探してみました。ほとんどが雲の中から昇ってきているものでした。 からっと晴れることは少ないようです。
もう一つ困ったことがあります。普通に海岸近くで海面から昇ってくる朝日や沈む夕陽の写真を探してみても、 日の出日の入り時から太陽光を反射してしているものはほとんど見つけられません。 尖った波がたっているときは、波の影の部分だけが見え、光の当たっている面が見えないので反射が見えないのでしょう。 少し昇ってくると、見え始めることが多いようです。
波がたっていると、太陽光の反射を分散させます。そのために、海面に映る太陽像は広がって見えます。前後方向に長く延びます。 この時でも、反射している中心位置は何となくわかりますから、この位置を基準にして太陽がどこに写っているか判断できるでしょう。 富士山頂からなら、太陽が直径の8倍以内の高さにあるときに海面に太陽像の中心が映っているのがわかれば、地球が丸いことの証拠といえるでしょう。 反射がみえないからといって、平らだとは言い切れないでしょう。波で映って見えていないのかも知れません。
簡単そうに見えて意外と難しい方法かも知れません。ただ高さの効果が2倍になっているので、 もう少し低い山でも海に昇る朝日や沈む夕陽がみられるところならば、証明に使えそうです。
この段2024.03.10記載
3-2' 夕陽に照らされる雲
夕方日没後に空を見ると、雲はまだ夕陽に照らされ赤く染まっています。それが時間がたつと、日が当たらなくなり暗くなります。 日の出の時は、これと全く逆のことが起こります。その時のようすに違いがあるかを考えてみることにします。
雲が暗くなるかならないかの境界の位置をAとします。 この位置が地球が平らな場合と丸い場合でどう違ってくるかを考えてみます。図で水色の所が地球です。★印の所から見るとします。 上側が平らな地球、下側が丸い地球を表しています。オレンジ色の太陽から出た光が地平線をかすっていきます。 それが雲(高さをhとします)に当たる所がA点で、ここより太陽側はまだ照らされていて(橙色で表示)、遠い側は日が当たっていません(くすんだ青色で表示)。 太陽が水平線より角度θだけ下に沈んだときに、影の境界線は観測者の真上からどれだけ離れているかを角度(α)として求めてみることにします。
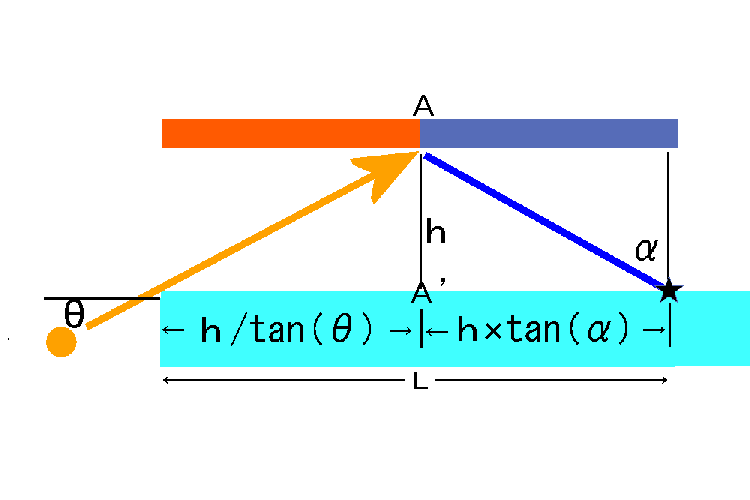
−−地球が平らな場合−−
観測者からまたは地平線から影の境界の真下の地面までの距離はそれぞれの三角形を考えることで求められます。その値は図に示したとおりになります。 この2つの数式の合計が地平線までの距離ですから、地平線までの距離を L とすると
L = h/tan( θ ) + h×tan( α )
α = atan( L/h − tan( 90°− θ ) )
参考 : 1/tan( θ ) = tan( 90°− θ )
と求められます。
 −−地球が丸い場合−−
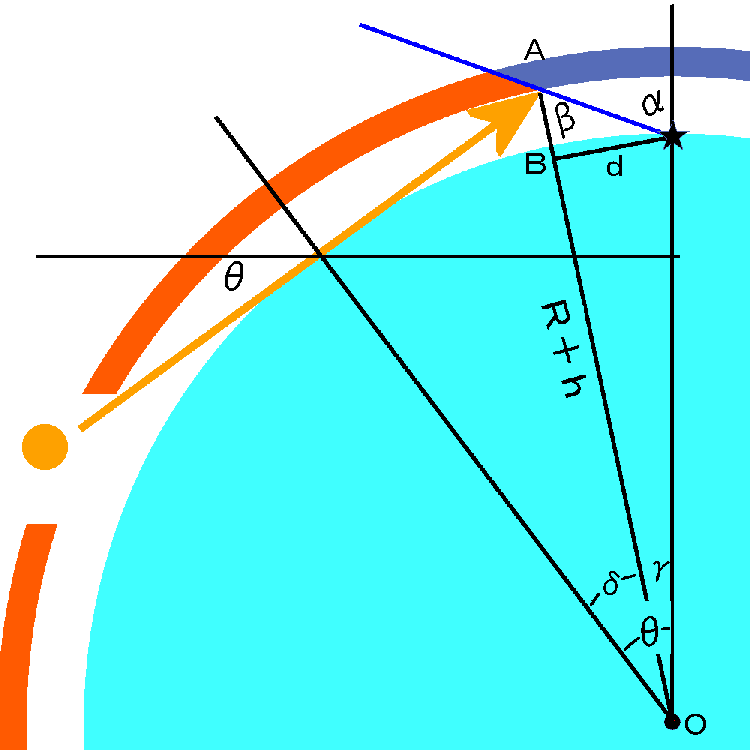
−−地球が丸い場合−−いくつかの角度や位置を表す記号を追加します。地球の中心がOで、半径がRです。 観測者の位置から線AOに下ろした垂線の位置がBでその長さをdとします。 また、A点から見たとき地平線と観測者の地球中心角をそれぞれδ、γとします。
まず図からわかるのは、観測者と雲から見た地平線の位置との間の地球中心角は、太陽高度と同じになります。
αβγの関係は、三角形の内角の和が180°なのを利用して、
になるのがわかります。
また地球中心の角度の関係から
です。
つぎにδを求めてみます。影角度と呼ぶことにします。
です。
次にβを求めてみます。図から
tan( β ) = d / (AB間長さ)
また
(AB間長さ) = R + h − (BO間長さ)
(BO間長さ) = R × cos( γ )
d = R × sin( γ )
なので
β = atan( Rsin(γ)/( R+h−Rcos(γ) ) )
これからαを求めることができます。
この式からだとどのような感じになるのかわからないので、表計算ソフトを使って求めてみることにします。
日没後の経過時間(分)ごと太陽高度と影の見える天頂角度の計算結果です。
| 地球が平らな場合 | |||||
| 分 | 太陽高度 | (rad) | 影まで距離 | 天頂角度 | (deg) |
|---|---|---|---|---|---|
| 0 | 0.00 | 0.000 | -90.00 | ||
| 1 | 0.25 | 0.004 | -2111.82 | -1.57 | -89.73 |
| 2 | 0.50 | 0.009 | -965.89 | -1.56 | -89.41 |
| 3 | 0.75 | 0.013 | -583.90 | -1.55 | -89.02 |
| 4 | 1.00 | 0.017 | -392.90 | -1.55 | -88.54 |
| 5 | 1.25 | 0.022 | -278.29 | -1.53 | -87.94 |
| 6 | 1.50 | 0.026 | -201.88 | -1.52 | -87.16 |
| 7 | 1.75 | 0.031 | -147.30 | -1.50 | -86.12 |
| 8 | 2.00 | 0.035 | -106.36 | -1.48 | -84.63 |
| 9 | 2.25 | 0.039 | -74.52 | -1.44 | -82.36 |
| 10 | 2.50 | 0.044 | -49.04 | -1.37 | -78.47 |
| 11 | 2.75 | 0.048 | -28.19 | -1.23 | -70.47 |
| 12 | 3.00 | 0.052 | -10.81 | -0.82 | -47.23 |
| 13 | 3.25 | 0.057 | 3.89 | 0.37 | 21.28 |
| 14 | 3.50 | 0.061 | 16.50 | 1.03 | 58.78 |
| 15 | 3.75 | 0.065 | 27.43 | 1.22 | 69.97 |
| 16 | 4.00 | 0.070 | 36.99 | 1.31 | 74.87 |
| 17 | 4.25 | 0.074 | 45.43 | 1.35 | 77.59 |
| 18 | 4.50 | 0.079 | 52.94 | 1.38 | 79.30 |
| 19 | 4.75 | 0.083 | 59.65 | 1.40 | 80.48 |
| 20 | 5.00 | 0.087 | 65.70 | 1.42 | 81.35 |
| 21 | 5.25 | 0.092 | 71.17 | 1.43 | 82.00 |
| 22 | 5.50 | 0.096 | 76.15 | 1.44 | 82.52 |
| 23 | 5.75 | 0.100 | 80.69 | 1.45 | 82.94 |
| 24 | 6.00 | 0.105 | 84.86 | 1.45 | 83.28 |
| 25 | 6.25 | 0.109 | 88.69 | 1.46 | 83.57 |
| 26 | 6.50 | 0.113 | 92.23 | 1.46 | 83.81 |
| 27 | 6.75 | 0.118 | 95.51 | 1.47 | 84.02 |
| 28 | 7.00 | 0.122 | 98.56 | 1.47 | 84.21 |
| 29 | 7.25 | 0.127 | 101.39 | 1.47 | 84.37 |
| 30 | 7.50 | 0.131 | 104.04 | 1.47 | 84.51 |
| 地球が丸い場合 | ||||
| 分 | 太陽高度 | 地心影角度 | 天頂角度 | (deg) |
|---|---|---|---|---|
| 0 | 0.000 | -0.06 | -1.57 | -90.00 |
| 1 | 0.004 | -0.05 | -1.57 | -89.74 |
| 2 | 0.009 | -0.05 | -1.56 | -89.45 |
| 3 | 0.013 | -0.04 | -1.56 | -89.14 |
| 4 | 0.017 | -0.04 | -1.55 | -88.77 |
| 5 | 0.022 | -0.03 | -1.54 | -88.35 |
| 6 | 0.026 | -0.03 | -1.53 | -87.84 |
| 7 | 0.031 | -0.03 | -1.52 | -87.20 |
| 8 | 0.035 | -0.02 | -1.51 | -86.35 |
| 9 | 0.039 | -0.02 | -1.49 | -85.12 |
| 10 | 0.044 | -0.01 | -1.45 | -83.12 |
| 11 | 0.048 | -0.01 | -1.38 | -79.14 |
| 12 | 0.052 | 0.00 | -1.17 | -66.77 |
| 13 | 0.057 | 0.00 | 0.43 | 24.88 |
| 14 | 0.061 | 0.01 | 1.27 | 73.02 |
| 15 | 0.065 | 0.01 | 1.41 | 80.85 |
| 16 | 0.070 | 0.01 | 1.46 | 83.92 |
| 17 | 0.074 | 0.02 | 1.49 | 85.59 |
| 18 | 0.079 | 0.02 | 1.51 | 86.67 |
| 19 | 0.083 | 0.03 | 1.53 | 87.43 |
| 20 | 0.087 | 0.03 | 1.54 | 88.02 |
| 21 | 0.092 | 0.04 | 1.54 | 88.50 |
| 22 | 0.096 | 0.04 | 1.55 | 88.90 |
| 23 | 0.100 | 0.04 | 1.56 | 89.25 |
| 24 | 0.105 | 0.05 | 1.56 | 89.55 |
| 25 | 0.109 | 0.05 | 1.57 | 89.83 |
| 26 | 0.113 | 0.06 | 1.57 | 90.08 |
| 27 | 0.118 | 0.06 | 1.58 | 90.32 |
| 28 | 0.122 | 0.07 | 1.58 | 90.54 |
| 29 | 0.127 | 0.07 | 1.58 | 90.75 |
| 30 | 0.131 | 0.07 | 1.59 | 90.95 |
雲の高さは、巻雲や巻積雲、巻層雲を考え10kmとします。地球半径は6370km、 地球が平らな場合の地平線までの距離は、日没後影が頭上を通過するまでの時間が地球が丸い場合と同じになるように180kmとしました。
計算式を確認します。その前に先ほどあげた数値の入っているそれぞれのセルに雲高度、地球半径、地平距離と名前をつけています。 これで計算式にこの文字があれば、自動的に数値が代入されるようになります。直接その番地を絶対参照してもかまいません。
計算式です。表の各列のセル番地はその列のタイトルの名前で表すことにします。 行は、同じ行にあれば同じ数値になります(平らな場合、丸い場合それぞれ別です)。
−−地球が平らな場合です−−
分から太陽高度の計算です。単純にするため赤道上春分秋分の日で求めています。
太陽高度=360*分/24/60
三角関数は度では計算できないので弧度法に変換します(radのセル)
太陽高度(rad)=太陽高度*PI()/180
影までの距離を計算します。結果がマイナスの場合は、東側にできていることになります
影まで距離=地平距離-雲高度/TAN((rad))
最後に影の見える方向の計算です。天頂角度の列に入力します。
天頂角度=ATAN(影まで距離/雲高度) (天頂角度には同じ行の「影まで距離」列のセル番地が入ります)
結果は弧度法で示されますので度(deg)に直します。
天頂角度(deg)=天頂角度*180/pi()
なお、日没後の時間が0の時は、0(tan(90゚))で割りますからエラーとなります。そのため計算式ではなく直接数値を入力しています。
−−地球が丸い場合です−−
まず図でδの角度は全てで共通ですから、先に計算をしておき、結果の入るセルに影角度と名前をつけておきます。
影角度=ACOS(地球半径/(地球半径+雲高度))
計算表に入ります。太陽高度は地球が平らな場合と同じですが、直接rad(弧度法)が出るようにしています。
次にγの角度です。地心影角度と書かれている列です。
地心影角度=H5-影角度
天頂角度の計算です。
天頂角度=ATAN(地球半径*SIN(太陽高度)/(地球半径+雲高度-地球半径*COS(太陽高度)))+太陽高度
地球が平らな場合と同様に度(deg)に換算しておきます。 結果がマイナスの場合は東側に、90°を越えている場合は地平線の向こう側なので雲に光が当たっているのが見えないことを示しています。
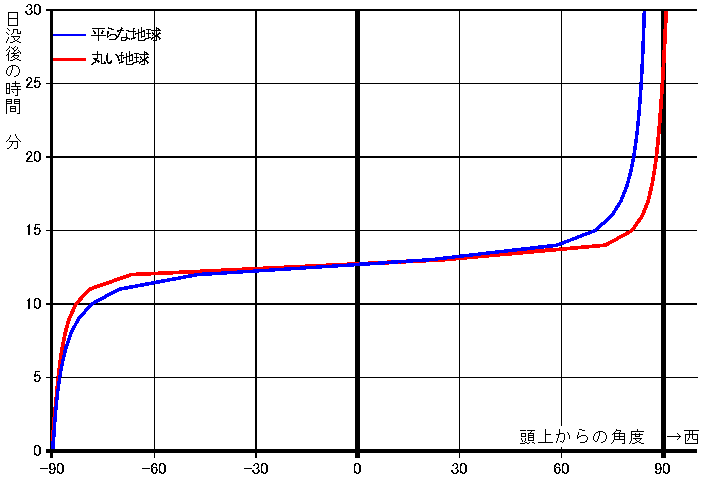 表のままだとわかりにくいので、グラフにしてみます。結果が右図になります。
表のままだとわかりにくいので、グラフにしてみます。結果が右図になります。どちらの場合も、頭上を通過(天頂角度が0°)するときの動きは速く、地平線近くではゆっくりしています。 違いをさがしてみることにします。地球が丸い場合は、日が沈んでから影が頭上に来るまでと、頭上に来てから地平線の彼方に見えなくなるまでは、 全く逆の動きになります。これに対して、地球が平らな場合は、頭上を通過してからは少しゆっくり目になり、 地平線近くまで来たときにはいつまでも日の当たっているところが残ります。
実際に、夕陽に照らされるようすを撮影しタイムラプス動画にしたものを左に示します。
撮影は2017年8月26日の午後6時50分頃からの約10分間のもので、これを約8秒に縮めています。 頭上付近は同時に入れることはできませんでした。一番高いところで天頂角度が30度くらいです。
見た感じでは、明るいところが地平線近くになるとなかなか暗くなりませんが、それでも気がついたら真っ暗になっています。 いつまでも、明るいところが残っているという感じではなさそうです。
2017.12.13
3-3 平面と球面上の幾何学
幾何学で三角形の内角の和が180度になることは証明できません。内角の和が180度になるのは特殊な条件に限られているからです。 その条件とは、平面上に置かれた三角形であることです。球面上なら180度にならないことは簡単に証明できます。 例えば、クイズであるように、「南に100km(100kmより10000kmの方がいいのですが)進み、 そこから東に100km進みさらにそこから北に100km進んだら元の所に戻ってきた。 始めの場所はどこか」という問題のように内角の和が180度を超えるといった例も考えられます(10000kmの時以外は東へまっすぐというの直線ではありません)。 このような、平面上の図形と、球面上の図形の違いを利用することで地球が丸いかどうかを調べることができるはずです。
子午線は北極で交わる 子午線とは、北と南を結ぶ線のことです。昔、北は子(ね)、南は午(うま)と呼んでいたことに由来します。 東経何度といった経線と同じものです。南北線は平行なので交わるはずはないのですが、地球儀を見ると、北極と南極に集まっています。 子午線が極で交わっているのを確認するのはかなり困難と考えられます。別の方法を考えることにします。 極で交わるということは、子午線の間隔が極に近づくにつれて次第に狭くなることを意味しています。 従って子午線の間隔が極に近づくにつれて狭くなっているか、一定であるかを調べれば、地球が丸いか、平らなのかを知ることができます。
正確な北を求めるためには精密な測量機器が必要です。奈良時代の条里制の跡が正確に南北になっている事から、 南北の方向を決めるのは簡単なように思えます。基本的には、太陽の作る影が最も短かくなる時の影の方向を北になることを利用して求めます。 ほんのわずかでもずれれば結果に影響してきます。北極星はわずかにずれていますのでそのままでは使えませんが、 日時と時刻がわかればどの方向にどれだけずれているかがわかるので、北(天の北極)の方角を求めることができます。 天体望遠鏡の極軸を地球の自転軸にあわせる、極軸あわせはふつうはこの方法で行われますが、東(または西) の空と南の空の星の動きを利用する方法もあります。正確に南北が求められたところで、 地形の起伏にあわせて延長していくのもかなりの困難が伴います。実際に測定するのではなく、専門家が行った記録を利用することにします。
国土地理院が、日本全国の地形図を発行しています。地図の区画は、基本的には等間隔の経線・緯線で区切って作られています。 例えば25000分の1の地形図では、経線間隔は7.5分(1度の8分の1)になります。北海道と沖縄でも同じ間隔になっていますから、 2地域の地形図を見比べれば経線間隔(=子午線間隔)の違いはわかります。北海道では、区画の形が正方形に近いのに対して、、 沖縄では横幅いっぱいで、記号の意味を書く欄もかなり狭くなっています。明らかに、子午線間隔が北ほど狭くなっていることがわかります。 1枚の地形図でも、地球が丸い影響が見られます。地形図の各辺の長さを測ってみればわかるのですが、図の右下側、 行政区画の書かれている欄に、各辺の長さが記入されています。例えば、昭和47年発行25000分の1京都西南部では、 上辺が45.62cmに対して下辺は45.67cmと0.5mmだけ長くなっています。辺の間隔の約0.1%にあたります。 ほんのわずかですが、子午線間隔が狭くなっていることが読み取られます。
子午線の間隔から、地球が丸いかどうかを判断しようとすると、約1.1km※1間隔の子午線が1km北側で1m狭くなるぐらいですから、 測定はかなり困難※2だと考えられます。
※1 大阪付近の地形図では、横と縦の辺の長さの比は、約46cm:40cm=1.15:1になっています。
※2 1km先で1m離れたものは0.3の視力があれば2つに識別可能です。
プレートの運動 平行線である子午線が一点で交わるのなら、平行に移動しているものもどこかでぶつかるはずです。 例えば、地球上のプレートの運動を考えてみましょう。プレート上で、プレートの運動方向に対して直角方向に離れた2地点があるとします。 この2点はどうなるでしょうか。平行に移動しているので、地球が丸い場合はいつかはぶつかることになります。 無理に動かすと地球からプレートがはがれていきます。こんな事は起こりえませんから、地球が平らだと言っていいのでしょうか。
じつは、地球上でプレートを動かす方法があります。例えば、丸いボウル(洗面器)に水が入っている状態を思い浮かべてください。 ボウルを水平面内で洗面器の中心を軸に回転(自転)させてやると、中の水は動かずに洗面器だけを動かすことができます。 この時の水が地球、ボウルがプレートと考えれば、プレートの動かし方が理解できます。地球の中心を通る軸を中心に回転させてやればよいのです。
回転軸は地球の表面を2カ所で通り抜けます。その近くでは、プレートの運動速度は遅く、離れるに従って速くなります。 地球が平らな場合でも、プレートが回転運動をすることは可能ですが、その場合、回転の中心は1カ所だけになります。 プレート回転運動の中心が、1カ所か2カ所なのかを調べれば地球が丸いかどうかがわかります。
プレートは巨大ですので、このように軸がいくつあるかが求められる前に、プレートの立体的な形の方が先にわかってしまいそうです。 地球が丸いという証明に使うというよりは、地球が丸いことを考えないと現象が正しく理解できない例と見た方がいいでしょう。
3-4 東に行けば戻ってくる
球面と平面とのもう一つの違いは、面上の直線の端が閉じていてないか、無限遠方までのびていく(実際には端がある)かです。 簡単に言えば、同じ方角に進み続けたら元の所に帰って来られるか来られないかの違いです。
どの方角でもいいのですが、例えば東にまっすぐ進んでいったとすると、地球が丸いのなら元の場所に帰ってくることができます。 15世紀から16世紀にかけて地球が丸いと信じる人たちに、地球一周をしてみようという気運が高まりました。 地球が平らだと信じていた人たちは地の果てにたどり着いたら、海水がものすごい勢いで落ちていて巻き込まれて大変なことになると、 航海に出るのをとどめました。それにもかかわらず、大海に出て行った人たちがいました。東にある場所でも、 西に進んでいったらたどり着けるはずだと進んで行って、西インド諸島にたどり着いたコロンブスをはじめとして、 その後世界一周を成功させたマゼラン一行に至るまでさまざまな人たちの活躍がありました。このあたりの話は世界史の専門家に任せるとします。 ここで、本論にとって一番大事なことは、これらの事件をきっかけに、 世界中(ヨーロッパ)の人たちのほとんどが地球は丸いものなのだと考えるようになったことです。
現在では、簡単に世界一周ができるようになったのも、当時の人たちが命がけで航海をして、 地球が丸いことを証明してくれたおかげといってもいいでしょう。
3-5 宇宙から見た地球の姿
地球が丸いと実感できるのはなんといってもその写真を見たときでしょう。気象衛星の全球雲画像は1時間毎に更新されていて、 見て確認することができます。「衛星写真は地球が丸いと信じ込ませようとする人たちの陰謀だ」といっていた人たちがいたそうですが、 そこまで極端ではなくても、多少の修正が入っていることを認識した上で、判断する必要があります。
地球全体を撮ったカラー写真は意外と少なく、ネットから入手できるものはアポロ宇宙船からのもの以外にはあまり見あたらないようです。 最近では、かぐやが撮った「地球の出」写真(まん丸ではなくサイズも大きくない)があります。地球から飛び立っていく宇宙船は、 地球を写しやすいタイミングを逃しているのでしょうか。はやぶさのラストショットもかろうじて撮影できた1枚のようです。
2015年7月7日のひまわり8号運用開始により、静止画像がカラーで見られるようになりました。
補足(2022.06.26)
宇宙から見た地球の姿からいえるのは、宇宙船から直角方向の面に投影した地球の形が円形であることです。 従ってこれだけでは地球が球形なのか、円筒形それとも童謡にあるようなお盆のような形なのかを区別できません。 もう一手間、何らかの説明が必要です。
ひまわりの全球画像で考えてみます。日本列島付近を拡大して見てください。こちらで形を示しています。 形が、ふだん見る日本地図とは少し異なっています。南北方向に縮んでいるのがわかると思います。 赤道上空にあるひまわりから見ると、地球が球形なために、真下の地点から離れるに従って地面が傾いていくためです。 見えている地球の周辺部に近づくほど縮みの度合いが大きくなっているというところまで確認して始めて地球は球形であるといえます。
地球がまん丸に見えている画像よりは、半月型・三日月型といった画像の方がいいでしょう。 地球表面が平面な場合は、全体が一斉に暗くなるため、このような明暗境界線はできません。
たくさんの画像を集めてみてどれもが円形に写っているから球形だと決定するという方法もあります。 国際宇宙ステーションから見た地球の動画でもいいでしょう。地平線の向こうから見えなかった地面が現れてくるようすをみると、 地球が球形に見えます。
最近はコンピュータグラフィックで作られた画像もあるので、球形という証拠として使うにはよく確認する必要があるでしょう。 その中でお気に入りなのは次の動画です。(2023.09.18閲覧)
Bautiful Night Aurora from ISS : https://www.youtube.com/watch?v=eBTiGdrvj2o
4.地球が丸いと起こる不思議
過去には、地球が丸いか、平たいかの論争があったようです。その中で地球は丸くはないという反論もいくつか出されました。 その論拠とそれが正しい主張であったのかどうかを検討してみることにします。
4-1 遠方の地面は落ち込んでいない
地平線付近の地面は落ち込んでいるようには見えない、地球はどこまでも平らに見える、だから地球は平らなのだという説明です。
地面が向こう側に下がって行く坂になっていたとします。あまり傾きがきついと、坂そのものが見えなくなります。 緩やかだと傾いているのがわかりにくくなります。遠くにあれば余計わかりづらいようです。おまけにそれが海面だと、 水平だと錯覚するようなしくみが働いているようで、平らに見えてしまいます。遠くの地面は水平だと思ってしまうだけのようです。 富士山から見た水平線のところであった説明を思い出してください。水平線は2度下の方向に見えます。 水平線付近の海面はこの線と平行になっているので、向こう側に2度下がっていることになります。 2度というわずかな角度ながら、しっかり向こう側に落ち込んでいることがわかります。 横に2度傾けても傾いているのはほとんどわからないでしょう。向こう側に2度というのはもっとわかりにくいものです。 山の高さが低くなり、傾斜角度が小さくなりもっとわかりづらくなります。
4-2 地球の裏側の人は落ちる
地表にいる人は、下に落ちていこうとする。落ちないのは地面が支えているからである。地球が丸い場合地球の裏側では、 上下がひっくり返っているから、落ちていく方向は地球から離れる方向である。地球の裏側にいる人は地球に支えられることもなく、 表側にいる人が感じる下の方向に落ちていくはずである。
もっともらしく感じられますが、一つだけおかしな所があります。それは、地球の表側でも裏側でも、 ものは同じ下に落ちていこうと考えることです。この考えに従うと次のようになります。今、手に石を持っているとします。 石を手から放すと下に落ちていきます。ところでこの石を大きくしていくとどうでしょうか。やっぱり下に落ちていくはずです。 もっと大きくして地球ぐらいの大きさにするとどうでしょうか。下に落ちないはずはありません。 ところで、非常に大きな石と地球との違いは何なのでしょうか。違いはありません。なら、地球も下に落ちていくと考えるのが当然です。 さらに、落ちていく地球上での物体の動きを考えてみましょう。どのようになるかは落下する飛行機中での状態を考えてみるとわかります。 飛行機を高高度から落とすことによって、無重力状態を作り出すことができます。 いっしょに落ちようとする地球の表面では重力が発生しないことになります。つまり、ものは落ちないのです。 なぜなら、地球も地球上の物体も同じ速さで落ちていくため、同じ位置関係を保ち、物体の方が速く落ちることはない。 このような矛盾が生じるのは、始めに考えていたことに何らかの誤りがあったからです。
従って「裏側の人が落ちるはず」に対する答えは、もしそのようになるのなら、大きな矛盾が生じる。 それは地球上で重力が発生しなくなることである。それでは、地球上の物体が落下するのはどうしてでしょうか。 地球が引っ張っていると考える以外に説明が付けられません。これは万有引力の考え方の一部であります。 万有引力が働いているためとも答えられなくはありません。ニュートンのエピソードでいわれているように 「リンゴが木から落ちるのを見て発見した」のなら、答えとして適切ではありません。 万有引力は、地球が丸く、裏側にいる人が落ちない事から導き出された事柄に過ぎないからです。
それでも、何らかの方法で万有引力の法則が説明できれば、地球の裏側にいる人が落ちない理由の説明として成立します。 そこで、難しくはなりますが、万有引力の法則を他の方法で導き出すことにします。
万有引力の証明 万有引力の法則はケプラーの法則と、ニュートンが導き出した運動の3法則を使うことで証明できます。 それぞれの法則を整理しておきます。全部で6つあります。
ケプラーの法則
第1法則(楕円軌道の法則):惑星の軌道の形は、太陽を焦点の一つに置くだ円形である
第2法則(面積速度一定の法則):惑星−太陽を結ぶ動径は一定時間に同一面積を描く
第3法則(調和の法則):太陽惑星間の平均距離の3乗と公転周期の2乗は比例する
ニュートンの運動の法則
第1法則(慣性の法則):力が加わらない限り物体はその運動を続けようとする
第2法則(運動方程式):物体にかかる力と加速度は同じ向きで、大きさは比例する
第3法則(作用反作用の法則):物体に力を加えた(作用)とき、物体から逆向きに同じ大きさの力(反作用)を向ける
順番に番号をつけて見ていきます。
(1) ケプラーの第1法則から、惑星の運動は一定ではなく、絶えず変化することがわかります。これに運動の第1法則を適用すると、 惑星は何らかの力を受けていることがいえます。
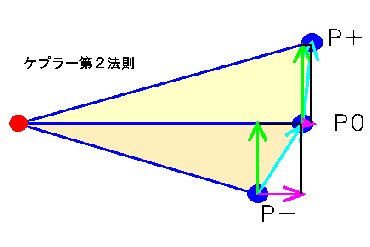 (2) ケプラーの第2法則に注目します(右図)。ある瞬間の惑星の位置をP0とします。その直前の位置をP−、
同じ時間だけ直後の位置をP+とおきます。この時、太陽S、P0、P−を頂点とする三角形の面積(薄橙色)と、
S、P0、P+の面積(薄黄色)はケプラーの第2法則により同じになります。ところで、SとP0を結ぶ線分は共通です。
これを三角形の底辺と考えると、高さにあたるP−、P+からこの線への垂線の長さ(緑矢印)は同じ長さになります。
これは動径方向に対して直角の方向です。図で長さは速度を表しますから、同じ長さであることから、
動径方向に直角方向の速度は変化していない事がいえます。運動の変化は、動径方向の速度(桃色矢印)が変化したのが原因といえます。
(2) ケプラーの第2法則に注目します(右図)。ある瞬間の惑星の位置をP0とします。その直前の位置をP−、
同じ時間だけ直後の位置をP+とおきます。この時、太陽S、P0、P−を頂点とする三角形の面積(薄橙色)と、
S、P0、P+の面積(薄黄色)はケプラーの第2法則により同じになります。ところで、SとP0を結ぶ線分は共通です。
これを三角形の底辺と考えると、高さにあたるP−、P+からこの線への垂線の長さ(緑矢印)は同じ長さになります。
これは動径方向に対して直角の方向です。図で長さは速度を表しますから、同じ長さであることから、
動径方向に直角方向の速度は変化していない事がいえます。運動の変化は、動径方向の速度(桃色矢印)が変化したのが原因といえます。(3) 動径方向の速度が変化したことと運動の第2法則から、この方向に力が加わった事がわかります。このような中心方向にかかる力を中心力といいます
(4) 惑星にかかる力が太陽から遠ざかる方向なら、惑星は次第に太陽から遠ざかっていき、ケプラーの第1法則がいうように、 いつまでも太陽の周りを回ることはできません。従って中心力は、太陽の方向に加わっていることになります(引力)。
 (5) 太陽が惑星を引っ張っているのなら、運動の第3法則から、惑星も太陽を引っ張っている事がいえます。
(5) 太陽が惑星を引っ張っているのなら、運動の第3法則から、惑星も太陽を引っ張っている事がいえます。−−ここまでで所期の目的は達成できましたが、公式まで続けることにします−−
簡単にするためにケプラーの第1法則の特殊な場合、円軌道を考えます。円軌道では、焦点は円の中心に一致します。 なお、文中の式には方向を表す矢印が上につくもの(ベクトル)がありますが省略しています。
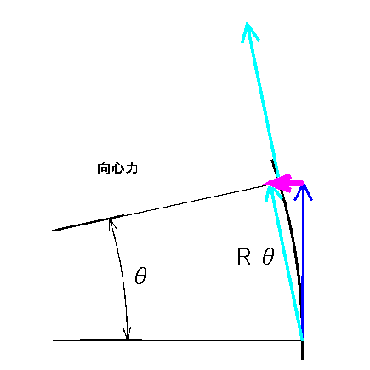
(6) 惑星が円運動をする場合に、中心方向に引かれている力の大きさ(向心力といいます)を求めます(右図)。 惑星の公転半径をR、惑星はある時間(t)内にθだけ回転したとします。ここでθを弧度法(ラジアン)で表したとすると、 この時間内に惑星が移動する距離はRθです。
(6-1) 円上では中心までの距離は一定ですから、ケプラーの第2法則から、運動速度の大きさは一定(Rθ/t)であることがわかります。 ここでθ/tをω(角速度)で表すと、
速度の大きさ(v)=Rω
(6-2) 運動の方向は接線の方向となりますから、運動を矢印(ベクトル)で表すと、始めは図の青矢印、 ある時間後は上の水色矢印のようになります。矢印の始点をそろえて書くと、先の位置の変化(桃色矢印)が物体に加わった加速度になります。 図で青矢印と水色矢印は角度θで交わっていますので、
加速度の大きさ(a)=v×(θ/t)=Rω×ω=Rω2
(6-3) 運動の第2法則(運動方程式)を用いるとき、力の大きさ(F)は、 物体の質量に加速度を掛けあわせたものになるように定義していますから、惑星の質量をmとすると
F=ma=mRω2
この式が向心力やその慣性力として働く遠心力の大きさを表す式です
(6-4) 惑星の公転周期をPとすると、一周が(2πラジアン)であることから
ω=2π/P
(6-5) この式を6-3式に代入して
F=mR・4π2/P2
(7) ケプラーの第3法則を式で表すと
P2=kR3 k:比例定数
(8) 6-5式に代入して
F=mR4π2/kR3
F=k2m/R2 k2:4π2/k
(9) 作用反作用の法則を適用すると、太陽は惑星から同じ大きさの力で逆向きの力を受けるので、 ある1点を中心に惑星と反対の位置で円運動をすることになる。
(10) 太陽の回転半径をr、質量をMとすると 6-3式と同様に
F=Mrω2=Mr4π2/P2
これは地球が受ける力に等しいから
F=Mrω2=mRω2
Mr=mR r=mR/M 質量と回転中心からの距離は反比例することがわかる
(11) 太陽-惑星間の距離は
R+r=R+mR/M=(1+m/M)R
惑星から太陽までの距離は、惑星の公転半径に係数をかけることによって求められる
太陽系の惑星の場合係数はほとんど1で、それは観測からも求められます。
(12) 10の最初の式にあるように8式にはMの項目が含まれないといけないから
F=GMm/(R+r)2 G:K2(M+m)2/M3
この式が、ニュートンの万有引力の公式です。
5.地球はなぜ丸いのか
地球の形が丸いのは、地球の重力が大きいためです。この条件を満たすのが、惑星やDwarf Planet(準惑星)です。 プリンを考えてみてください。容器に入ったものを皿に移したときに、下の方がつぶれて横に広がります。 上に乗っているプリンの重さに下のプリンが耐えられなくなってつぶれてしまったからです。 このようなことがあるので、極端に大きなプリンを皿に盛ることはできません。一般的にはバケツサイズが限界といわれています。
岩石も同じで、地球上であまりに高く積み上げると、岩石自体の重さに底の岩石がつぶれてしまいます。そのために大きな山が作られないのです。 10000mほどが限界といわれています。この高さは地球の半径に比べて非常に小さな数値です。 真偽のほどはわかりませんが、あまりに深く掘った鉱山では、岩石の圧力で、坑道が何の前触れもなくつぶれてしまう事があるそうです。 本当なら、高い山がつぶれるのと原理は同じと考えられます。
地球が丸い原因はもう一つあります。本当はこちらの方が大きく関わっています。それは地学の教科書に必ず載っている「アイソスタシー」 が関係しています。この理論には、マントルは液体と同じように振る舞うということが含まれています。 もし液体なら、表面は重力の方向に対して直角になりますから、海面と同じように球形になるのは当然です。 地殻の表面はそれより上にはあまり飛び出すことができませんから球形にならざるを得ないのです。
アイソスタシーについては別に詳しく述べることにします。
表紙 目次 先頭
2012年 3月 掲 載 開 始
2012年 5月 加筆 一応完成
2013年 4月 カノープスの写真を追加
2014年 5月 遠ざかる船写真解説追加
2014年 8月 日周運動の写真解説追加
2016年 3月 カノープスの写真を変更
2017年 6月 3節3-2項補足2ヶ所追加
2017年12月 3節3-2項補足3-2'項追加
2022年 6月 3節最後 補足 追加
2024年 3月 3節3-2項に朝日が…追加
2012年 3月 掲 載 開 始
2012年 5月 加筆 一応完成
2013年 4月 カノープスの写真を追加
2014年 5月 遠ざかる船写真解説追加
2014年 8月 日周運動の写真解説追加
2016年 3月 カノープスの写真を変更
2017年 6月 3節3-2項補足2ヶ所追加
2017年12月 3節3-2項補足3-2'項追加
2022年 6月 3節最後 補足 追加
2024年 3月 3節3-2項に朝日が…追加