人工衛星にまつわる様々な計算をしてみました。 求めたのは、｢空を通過する時間｣｢明るさ｣｢日没後出現できなくなるまでの時間｣｢静止衛星の仰角｣です。

１．人工衛星の飛行高度と見える時間
　日没後や夜明け前に人工衛星を見ることがあります。ゆっくりと動いているように見えます。 一体どれくらいの時間見えているのでしょうか。 地平線にでてきてから天頂を通って反対側の地平線に沈むまですっと見えているとしてその時間を考えてみます。 人工衛星の飛ぶ高さや向きよって変わってきますが、概算で計算してみることにします。大気差の影響も無視することにします。
　人工衛星は、地球の自転の勢いを利用しさらに加速をつけて飛び立ち地球の周りを回っています。そのため、西から東に進むのが一般的です。 実際には、多少南北方向にずれた方向に動くものもあります。赤道上で西から東に進むものと、南北方向に動くものの両方を考えてみることにします。
　計算を簡単にするために、地球を赤道半径の６３７８kmの球形とします。人工衛星の軌道も円形とします。
　人工衛星の飛行高度を ｈ 、地球の半径を Ｒ とおくと、人工衛星の軌道半径は Ｒ＋ｈ です。
　人工衛星が水平線上に見えるとき、その位置と観測点を地球中心から見たときに離れて見える角度をθとすると、次の関係式ができます。
 
(１)　(Ｒ＋ｈ)cosθ ＝ Ｒ→θ ＝ arccos(Ｒ÷(Ｒ＋ｈ))
 
　次に人工衛星の公転周期を求めます。公転周期は Ｔ (時間)とします。
　求め方は、ケプラーの第３法則を利用します。軌道半径と公転周期のわかっているものが必要です。 静止衛星は赤道上空３５７８６kmにあります(WikiPediaによる)。公転周期は２３.９３時間ですから、
 
(２)　Ｔ^２÷( Ｒ＋ｈ )^３ ＝ ２３.９３^２ ÷ ( ３５７８６ ＋ ６３７８ )^３
 
　　　Ｔ ＝ ✓ ２３.９３^２ ÷ ( ４２１６４ )^３×( Ｒ＋ｈ )^３
 
となります。
　人工衛星が南北方向に移動する場合は、この周期でまわっているようにみえます。　 ２θだけ回転する時間を求めると、南北方向に動く人工衛星に見える最大時間が求められます。つぎの式になります。
 
(３)　Ｔ × ２θ ÷ ２π　→ Ｔ × θ ÷ π
 
　人工衛星が東に進む場合、地球の自転速度分だけ少なくなります。見かけの公転周期をＳとおくと次の関係式ができます。 この式は惑星の会合周期の関係式と同じです。
 
(４)　１／Ｓ ＝ １／Ｔ − １／２３.９３
 
　　　Ｓ＝１／((１／Ｔ) − (１／２３.９３))
 
これから、赤道上で真西から昇り天頂を通って真東に沈む人工衛星の見える時間は、
 
(５)　Ｓ × ２θ ÷ ２π → Ｓ × θ ÷ π
 
で求められます。
　実際には天頂を通ることは少なく、一瞬だけ顔を出すものから様々です。動く速さの検討をつけるだけだと、これでわかると思います。
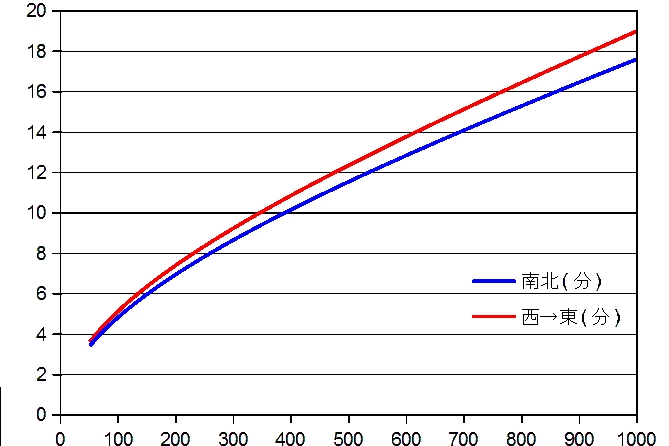
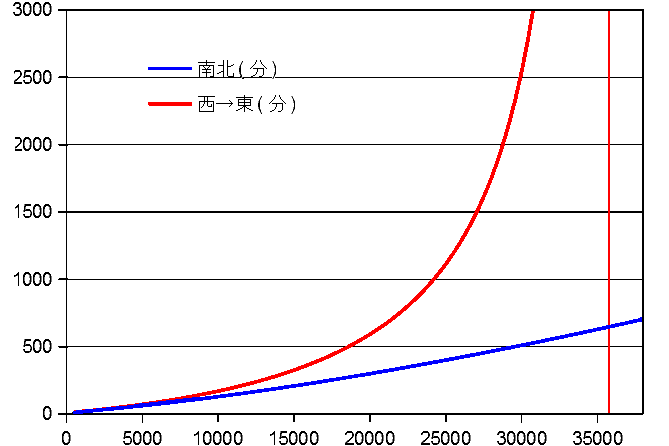
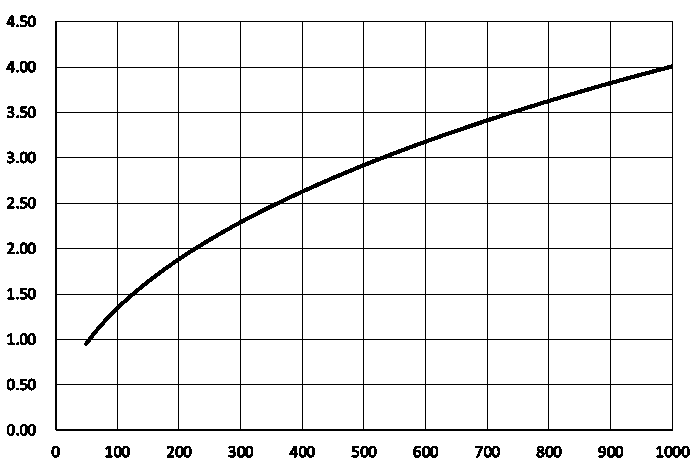
　計算は、表計算ソフトでやらせるのがいいでしょう。いろいろな高さのものを求めることができます。 これからグラフが作れます。次のようになりました。横軸が高度、縦軸が時間(分)です。 １つ目が高さ１０００kmまで、２つ目が３８０００kmまでのものです。２つ目のグラフの右側赤縦線は、 この高さで静止軌道のため見える時間は無限大で、これより上空の人工衛星は逆回転になるためにこういう引かれかたになります。


２．人工衛星の高度と見かけの明るさ
　最初に、人工衛星の明るさが飛行高度によってどのように変わるか考えてみます。 実際には、人工衛星の大きさや形、反射率、見かけの高度などによって変わってきます。 基準になるものを考えそれと比較して見ることにします。 基準として妥当かどうかわかりませんが、とりあえず頭上１００kmの距離にある人工衛星の等級が１等だとします。 違っていても、たとえば２等の場合その数値の差を加えれば求めることができます。

　明るさは、距離の２乗に反比例します。明るさから等級に変換する式があります。 組み合わせることで、距離 Ｄ にある人工衛星の等級 Ｍ を求めることができます。次の式です。
 
(６) 　Ｍ ＝ １ ＋ ５×log₁₀(Ｄ÷１００)
 
　頭上(天頂)にいるときは、人工衛星の高度(ｈ)をそのままＤに入力すれば求めることができます。水平線近くにいるときは距離は遠くなっています。 水平線上にいる人工衛星までの距離(Ｄ)と、先ほど使ったＲ、θとの間の関係式は次のようになります。この値を代入することで明るさが求められます。
 
(７)　Ｄ ＝ Ｒ tan(θ)
 
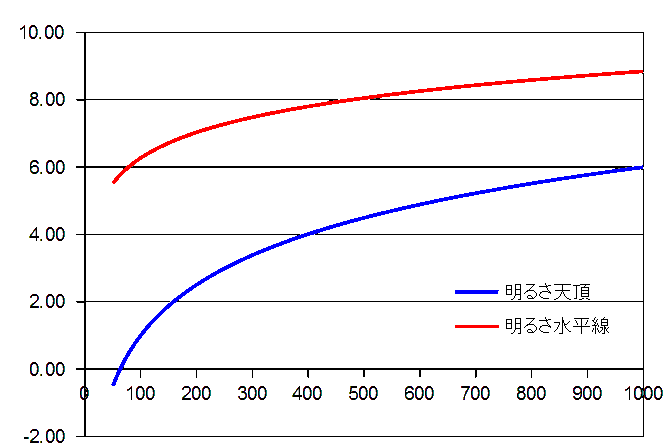
これも、表計算ソフトでいろいろな飛行高度でどうなるかを計算させ、グラフにしてみました。縦軸が等級、横軸が飛行高度です。 これも、１つ目が飛行高度１０００kmまで、２つ目が３８０００kmまでのものです。 国際宇宙ステーションは、約４００kmの高さで−３等ぐらいですから、７等分ほど明るい方にずれていることになります。 これほど大きな人工衛星は他にありません。大きさが１０分の１の場合、このグラフから１等ほど明るくするとだいたいの値を指しているのではないでしょうか。

＜昇ってくる途中の明るさの変化＞
　人工衛星が昇ってくるに従ってだんだん明るくなっていくのがわかります(右写真)。 その時見かけの等級と見かけの高度(仰角)との関係を計算してみます。 この場合も人工衛星の大きさや反射率で見かけの等級が変わってきますから、人工衛星が天頂にあるときは１等級の明るさとして計算します。

　まず、見かけの高度がｋ(度)の時の飛行高度ｈの人工衛星までの距離を求めます。 この時、地球の中心から見ると観測者と人工衛星は角度θ'離れて見えるものとします。
　観測者がそのまままっすぐ上にあがっていくと、人工衛星が同じ高さにあるように見えるところがあります。 この場所から地球の中心までの距離から次の式ができます。
 
　　　( Ｒ＋ｈ )×cos( θ') ＝ Ｒ ＋ Ｄ×sin( ｋ )
 
この時の観測者と人工衛星までの距離から次の式ができます。
 
　　　( Ｒ＋ｈ )×sin( θ') ＝ Ｄ×cos( ｋ )
 
　sinの２乗とcosの２乗の和が１になる関係を利用して２つの式からθ'を消去すると
 
　　　( Ｒ＋ｈ )^２ ＝ ｛ Ｒ ＋ Ｄ×sin( ｋ ) }^２ ＋ Ｄ^２×cos^２( ｋ )
 
Ｄについて降べきの順に並び替えると
 
　　　Ｄ^２ ＋ ２×Ｄ×Ｒ×sin( ｋ ) − ２×Ｒ×ｈ − ｈ^２　＝ ０
 
判別式を用いて
 
(８)　Ｄ ＝ −Ｒ×sin( ｋ ) ＋ ✓ Ｒ^２×sin^２( ｋ ) ＋２×Ｒ×ｈ ＋ ｈ^２　
 
が求められます。ｋに９０度を入れるとＤ＝ｈ、０度を入れると(７)式になります。

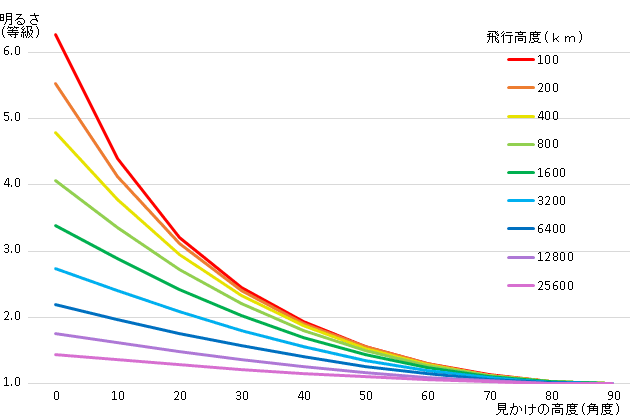
　これと(７)式を用いて、表計算ソフトで計算させてグラフにしたのが右の図です。 縦軸が見かけの明るさ(等級)で、横軸が見かけの高度(仰角)、飛行高度毎に色を変えて記入しています。 飛行高度が高いほど、見かけの高度による明るさの差は小さくあまり変化しないことがわかります。



３．日没後出現できなくなるまでの時間
　人工衛星が動いている間に消えることがあります。地球の影に入ったからです。 このような影があることは、日の出前・日没後に太陽と反対側の空に見ることができます。 また月食の時に月面にその一部が映されていることからもわかります。 人工衛星は太陽の光を反射して光っているので、この影に入ると見えなくなります。

地球の影で消える国際宇宙ステーション ２０２１年２月４日１８時３１分 １０秒間隔８秒露出の写真を比較明合成

皆既月食で見られる地球の影 ２０１１年１２月１０日２２〜２５時の写真を貼り合わせ

日の出前の地球影とビーナスベルト ２００７年８月１日５時５分 石鎚山弥山山頂から

　地球の影は、日没直後に東の空から昇ってきます。人工衛星の飛行高度が低いと空全体を覆うだけの大きさがあります。 影が空全体を覆ってしまえば、人工衛星はどこにあっても見えなくなります。そのようになるまでの時間を考えてみることにします。 緯度が大きくなると、計算式が複雑になります。とりあえず赤道上で真西から真東に進む人工衛星の場合を考えてみることにします。
　まず、影に入る場所を消滅点と呼ぶことにします。日没の瞬間には消滅点は真東の地平線延長上の空にあります。 この時、地球中心からみると消滅点と観測者は(７)式で求めたθ離れています。
　これから時間がたっていくと、消滅点は空に昇ってきます。 このとき消滅点より東側にある人工衛星は、太陽の光が当たっていませんから、見ることはできません。 消滅点が西の地平線延長上に来たときは、人工衛星の見える軌道は全て地球の影に入っています。 こうなると、軌道上の人工衛星はどこにあっても見ることはできなくなります。
　西の地平線上にいるときも、地球の中心から見た角度はθです。 地球が２θ回転すると、空に人工衛星が見えなくなる時間がやってくることになります。 いままでと同じように、いろいろな高度で人工衛星が全く見えなくなるまでの時間を表計算ソフトで計算しグラフにしてみます。
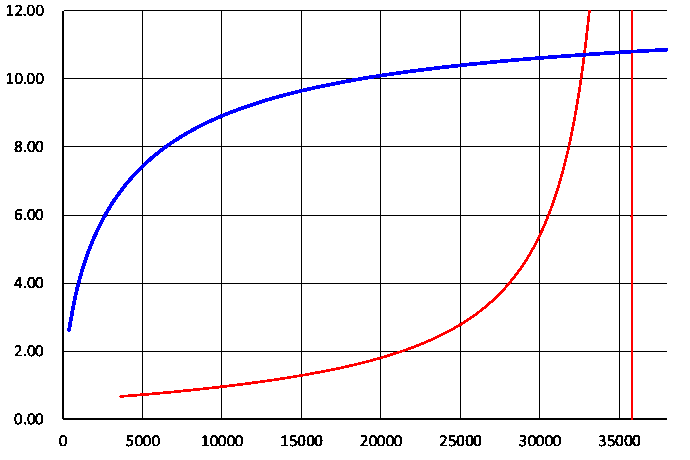
　下がその結果です。１０００kmまでと３８０００kmまで(青線)の２つの図を作りました。横軸が高度、縦軸が時間です。 　計算をしてみると、約２７００km以上の高さの人工衛星では、６時間以上かかるのかわかります。これは、消滅点が西の空に沈んだときには、 反対側の消滅点が東の空から昇ってきていることになります。この高さに人工衛星が無数にあると、どれかは必ず見えていることになります。 地球の影が見えたらで話をすると、空に丸い影が見えているはずです。
　この影の中を、人工衛星が通過するのにかかる時間を計算させてみます。地球中心から見たとき、影の半径(角度)は次の式で求められます。
 
(９)　arcsin( Ｒ ÷( Ｒ ＋ ｈ ))
 
人工衛星の動いて見える速さとこの角度から、通過に要する時間が計算できます。表計算ソフトで計算させ先ほどの図に赤線で入れています。

４．静止衛星の仰角
　静止衛星が、どの位置に見えるのか計算してみます。観測者と同じ経線上に静止しているものとします。
　静止衛星の仰角を Ｅ 、観測者の緯度を Φ とします。次の関係式が作れます。
 
(10)　Ｒ × sin( Φ ) × tan( Ｅ ＋ Φ ) ＝ Ｒ ＋ ｈ

　静止衛星の位置は、赤緯を使って表すこともできます。赤緯を δ として次の式でもとめられます。
 
(11)　δ ＝ Ｅ ＋ φ − ９０
 
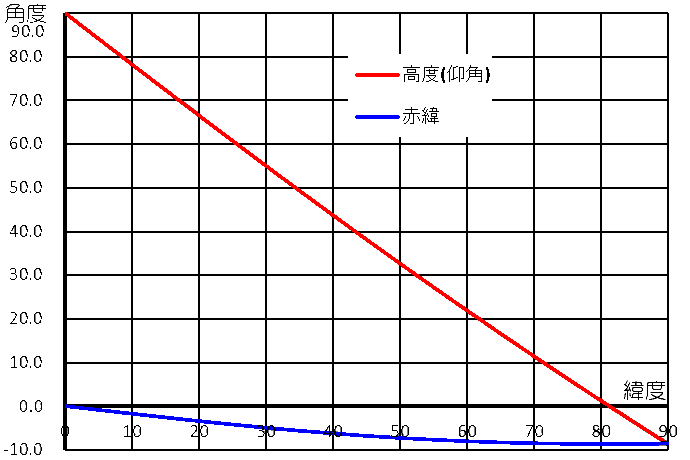
　緯度ごとにどのようになるかを表計算ソフトで計算させ、グラフにしてみました。横軸が緯度、縦軸が角度です。 赤線が仰角、青線が赤緯になります。北緯３５度では、仰角は５０度、赤緯は−５度になります。
　緯度８２度以上では、仰角がマイナスになっています。静止衛星は水平線下で見えないことを示しています。 さらに、静止衛星からの電波も受け取ることはできないので、衛星放送も受信できないでしょう。