ヨッシンと 地学の散歩
散歩道の四方山話
散歩道の四方山話
海面の高さは、時間をおいてみると変化していることに気がつきます。特に砂浜や、干潟で海岸の位置を見ると､ 防波堤の近くまで海が迫っているときがあるかと思えば、沖合遠くまで干潟や砂浜が広がっているときもあります(右写真)｡ 防波堤の近くまで海迫っているときは海面の高さは高く、逆に干潟や砂浜が広がっているときは、海面の高さが低くなっています｡ 実際には、高さはどのようにどれくらい変化しているのでしょうか。気象庁や海上保安庁のホームページから､ 海面の高さを毎時間測定した観測結果を入手することができます｡ 海面の高さの例として気象庁のホームページから、伊豆半島先端にある石廊崎での２０１０年１月はじめの観測結果をダウンロードしてみると､ 以下の表のようになっています(１５日分のうち７日分を表示)。３桁の数字が、基準面から海面までの高さです。大きな数字は海面が高かったことを示しています｡ 数字を見ると、大きなものから小さなものまで様々です。
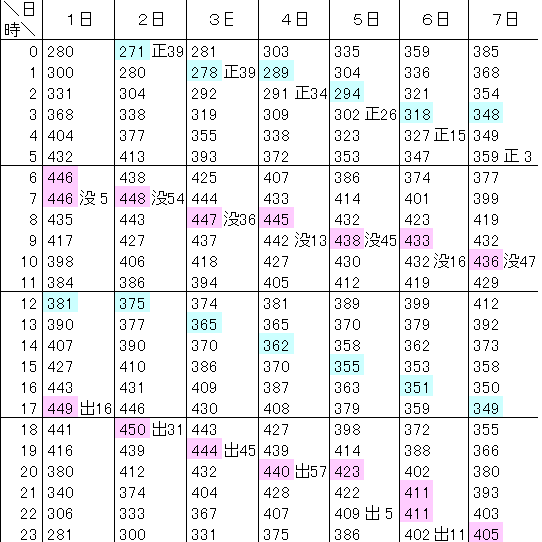
満潮や干潮は毎日決まった時刻に起こっているわけではありません。１日ごとに１時間弱遅くなっていくのを読み取ることができます｡ 月も同じように、毎日約４０分遅れて昇ってきます。そこで、月の昇ってくる時刻(出)、南中する時刻(正)、沈む時刻(没)の分の位を､ 海上保安庁のホームページから検索し、その時間の枠下段に記入してみました。その横に枠にはその現象の名前を略号で記入しています｡ 明らかに、月が地平線上にある頃には満潮になっていること、真南にある頃には干潮になっていることがわかります｡ 月の欄に印のない干潮は、月が沈んでから昇ってくるまでの真ん中あたりにありますので、この時に月が地平線下で､ 最も低くなっている時と考えていいでしょう。
おかしいのではと感じる人がいるかも知れませんが、とりあえず話を進めます。理由は 後で説明することにします。
これからの説明では、潮位の上下を逆にした方が全ての点でつじつまが合うのですが、どう読み取っても、満潮干潮を逆にすることができません｡ 本当は、この点だけが説明できるほうがかえってやっかいです。
月と満潮干潮の関係を見る上で、気象庁のデータを使ってもう一つ表を作ってみました。２０１０年１月石廊崎での､ 干潮時の潮位と満潮時の潮位差のいちばん大きな値です。表に月の形も入れています。朔、上、望、下はそれぞれ新月、上弦、満月、下弦です｡
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
潮位の差も、周期的に大きくなったり小さくなったりしています。潮位の差が大きいときが大潮で、干潮時の海面はいちばん低くなります (潮が引く)し、満潮時の海面は一番高くなります(潮が満ちる)。逆に潮位の差が小さいときが小潮で、海面の高さはあまり変化しません。
満月や新月の時は大潮で、上弦や下弦の月の時は小潮になっていることもわかります。
このように見てくると、潮位と月には何らかの関係があることが推定できます。それは何でしょうか。
次のホームページからデータを入手しました
気象庁(海面の高さ)：http://www.data.kishou.go.jp/kaiyou/db/tide/genbo/genbo.php
海上保安庁( 〃 )：http://www1.kaiho.mlit.go.jp/KANKYO/TIDE/real_time_tide/htm/kck_main.htm
〃 (月の暦)：http://www1.kaiho.mlit.go.jp/KOHO/automail/sun_form3.htm
国立天文台( 〃 )：http://www.nao.ac.jp/koyomi/koyomix/koyomix.html
月のどのような力が、潮汐を起こしているのでしょうか。何となく引力が関係しているように思われます｡
右写真はＪＲ九州長崎本線の車窓から撮ったものです。有明海では干潮と満潮の差(干満の差)が大きく、干潮時には干潟が沖合遠くまで広がります｡
ふつうに干満の差が大きいと書いていては単純すぎるということで、このような文章ができたのでしょう。引力との関係を見ていくことにします｡
単純に考えてみると、月の引力が海面を引っ張り上げているように思われます。それで考えてみると、地球の裏側では、海水が持って行かれるので､
海面が下がることになります。結局、月が１回昇って沈んで再び昇ってくるまでの間には干潮満潮がそれぞれ１回ずつ起こることになります｡
実際には、２回ずつあるのでうまく説明ができません。地球の表側が満潮の時､裏側も満潮になっていないといけないのです｡
何が間違っていたのでしょうか。次のように考えてみることにします。海面が月の引力で持ち上がられるとすると､
海水だけに引力が加わっているわけではありませんから、周りの山や海岸も一緒に持ち上げられます｡
海水も山も同じ高さだけ持ち上げられるので、海面と山や海岸との間には高さの差ができません。見かけ上海面が持ち上がらないのです｡
このように考えてみると、海面が引力によって持ち上げられるという考えは誤りだとわかります。地球の裏側も満潮になっている理由を、地球と月が互いに公転していて、その遠心力で説明しようとしているものもあります｡ (｢新しい高校地学の教科書｣BLUE BACKS 等 間違いである理由は別途解説します) 表側で海水が持ち上げられない以上、裏側の現象だけを考えるのは無意味です。この説明も誤りです。
それで、次のように考えてみることにします。まず、月からの距離がそれぞれ異なるように置かれた３つの物体があるとして考えます(右図上:緑丸青丸)｡
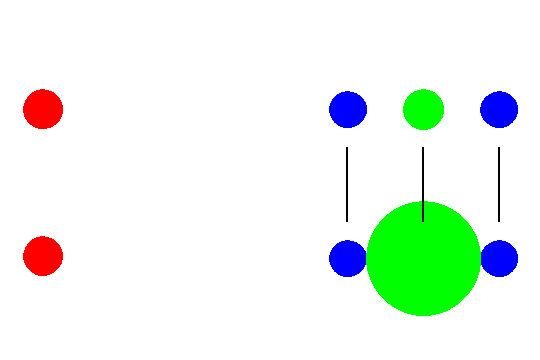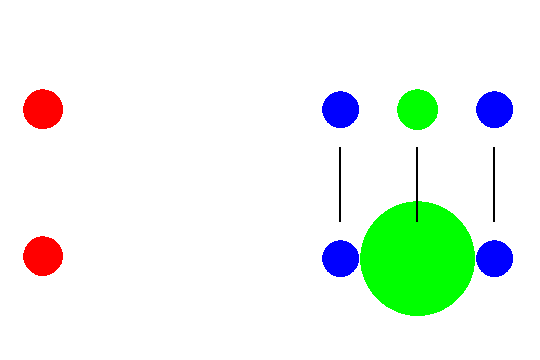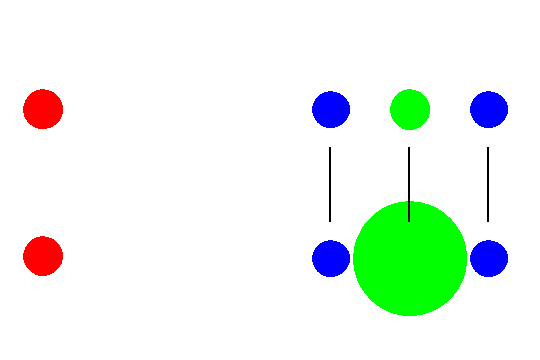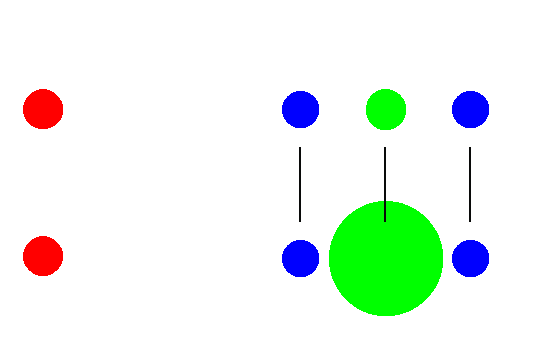それぞれの物体にかかる月からの引力は、月(赤丸)からの距離の２乗に反比例しますから(万有引力の法則)、月に一番近い物体にはいちばん大きな引力が働きます｡
その分速い速度で月に近づいていくことになります。逆に、いちばん遠い物体は引力が小さく、引き寄せられる量は小さくなります｡
ここで３つ並んだ真ん中の物体の質量はそのままで、その表面が両側にある物体と接するようにしてみましょう。物体の形は変化しないものとします｡
しばらくすると、先ほどと同じように、月の方に向かって落ちていきます。この時、中央の物体に接していた物体は､
中央の物体の表面から離れていくように見えます。この場合の中央の物体(緑丸)は地球､
両脇にある物(青丸)体は地球の表面にある海水と考えてみるとどうでしょうか。月のある側とその反対側の海面が地球から離れていく
(海面が持ち上げられている)ことが理解できます。実際には月より地球の方がはるかに大きく、地球が落ちていっているとは考えにくいのですが､
月からの引力が働いている以上は、間違いなく月に引っ張られて、月の方に落ちているのです(ぶつからないのは的＝月から大きく外れるためです)。地球の表面にある海水と、地球とでは、月から受ける引力の大きさが違います。違い(差)の大きさに相当する力で引き伸ばされます｡ この引き伸ばそうとする力のことを起潮力といいます。起潮力の大きさを数式から求めることは、ちょっとなれた人には簡単にできます｡ 質量ｍの物体にかかる起潮力の大きさは万有引力の大きさの公式を利用します｡ 万有引力の公式は、Ｆ(Ｒ)＝ＧＭｍ÷Ｒ２ (Ｒ：２つの物体間の距離、Ｇ：万有引力定数、Ｍ：月の質量)です｡ これに、月−地球間の距離をＤ、地球の半径をｒと置いてみます
起潮力＝距離Ｄと距離Ｄ−ｒとでの万有引力の差
＝Ｆ(Ｄ)−Ｆ(Ｄ−ｒ)
式を代入
＝ＧＭｍ÷Ｄ２−ＧＭｍ÷(Ｄ−ｒ)２
通分して一つの式に
＝ＧＭｍ{(Ｄ−ｒ)２−Ｄ２}÷{Ｄ２(Ｄ−ｒ)２}
{ }内を展開
＝ＧＭｍ{−２Ｄｒ＋ｒ２}÷{Ｄ２(Ｄ−ｒ)２}
式を整理して
＝−ＧＭｍｒ{Ｄ＋(Ｄ−ｒ)}÷{Ｄ２(Ｄ−ｒ)２}
ｒ<<Ｄ の時 Ｄ−ｒ＝Ｄとできるから
＝−２ＧＭｍｒ÷Ｄ３
式が−(負)になっているのは、月の方向に働いていることを指しています。
地表にある質量１ｋｇの物体が、月から受ける起潮力は０．０００００１１Ｎ(１.１×１０−６)で、赤道での遠心力０． ０３４Ｎに比べて小さいのですが、それ相当の影響を受けることになります(遠心力ぐらいの大きさもあれば２０kmも海面が持ち上がることになる) 。この式のＤとＭの値として、他の天体までの距離と、質量を入れてみるとその天体が及ぼす起潮力が計算できます。実際に計算してみると
数値だけ見比べてください。１０の右肩にある数値がマイナスで大きな程小さな値になります。
月に比べて太陽はだいたい半分、他の惑星は問題にならないくらい小さいことがわかります。従って、海面を上下させる潮汐作用を起こす天体は､ 月と太陽だけを考えればよいことになります。次で、月と太陽による潮汐の作用を考えてみることにします。
大潮 潮位の高さを考えるとき、月と太陽の起潮力を足し合わせたもので考えることができます。月と太陽の起潮力が合わさると､ 潮の満ち引きが大きくなります。この時の潮の状態が大潮です。月が単独で起こす潮汐の1．５倍の大きさで潮の満ち引きが起こります｡ このような状態にになるのは月と太陽が同じ方向にある、つまり新月の時と、正反対の方向にあるとき、これは満月の時です｡ これに対して、月と太陽の起潮力が打ち消し合うと、起潮力が弱まり干満の差が小さくなります。この状態が小潮です｡ この現象が起こるのは月と太陽が９０度離れているときで、この時月の形は上弦または下弦の半月です。 小潮の時の起潮力は、月だけの起潮力に比べ半分の起潮力になりますので、大潮ではその３倍の起潮力があることになります。
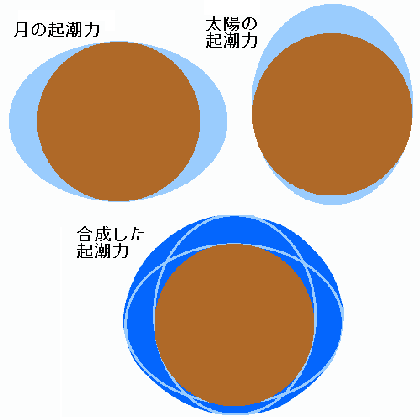
春の大潮 １年のうちで潮がもっとも引くのは何月でしょうか。１ヶ月の中では大潮の時に潮がもっとも引きます｡ だから、大潮の中でいちばん引くのは何月かを考えればいいことになります。ところで大潮の時の潮位はどのようになっているのでしょうか｡ 月の公転面は地球の公転面に対してほとんど傾いていません。そのため、大潮の時は、月と太陽の起潮力の方向が全く同じになります｡ 海面の形は、起潮力の方向に引き伸ばされた形になります。極端に言えばラグビーボールのような形になっています｡ 潮位の高さを考えるときは、ラグビーボールを斜めにおいて水平に切った切り口を考えると見当をつけることができます｡
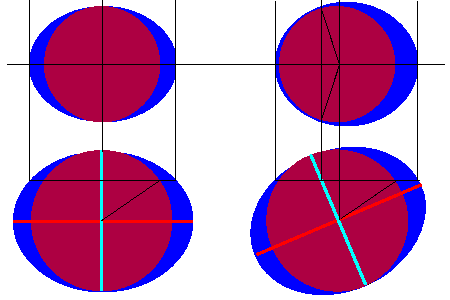簡単な図を書いて考えてみることにします(右図)。下段２つの図は地球を横から見た図で、上の図は北緯３５度の地点が通る所で切った切り口です｡
左の図は、春分秋分の頃、右の図は冬至夏至の頃の状態です。茶色が地球、青色は海水です。海水の膨らんでいる(赤線の延長)方向に月があります｡
潮位の高さは、上段の図の地球の中心から外側に向かって線を引き、青い部分を横切る長さに相当します。外に向かう線の方向は､
太陽に対するその時刻の方向です。右(または左)が太陽の方向ですので一致していると正午になります｡
図からわかることがいくつかあります。春分秋分の頃の干満は、１日２回規則正しく行われるのに対して、冬至夏至の頃は満潮時２回の高さは､
同じではありません。また高い方の満潮から干潮にかかる時間は６時間より長くなっています(夏至の日の昼間の時間の半分と同じ)。
いちばん潮が低くなるのは、下段の図に水色で線を引いたところです。左右どちらの図も北緯３５度の地点(横黒線)が横切っています｡
これは、大潮の日の干潮時の潮位は１年を通じて変わらない事を示しています。一般に春分秋分の頃の大潮は、干満差が大きいといわれます｡
この頃の干潮時だけ沖合の浅瀬が干上がり陸化する場所があという事を耳にしたことがありますが、本当にこの時期だけなのかは確認できていません｡
少なくとも起潮力のみで考える限りでは、干潮時の潮位は一年中変わらないといえます。春になり、潮干狩りのシーズンになって、干潟に出る機会が多くなって､
そういう現象をよく見かけているためだけなのかもしれません。潮が引くのは、他にもいろいろな要因がありますので、それが重なったときに､
最低潮位となります。本州から九州にかけての太平洋岸では冬から春先にかけては冬の季節風の影響で最も低くなり､
海上保安庁も注意を呼びかけています｡
(http://www1.kaiho.mlit.go.jp/KAN5/press/2009/10/01.html または http://www1.kaiho.mlit.go.jp/KAN10/yousu/suisan/teicho.pdf)鳴門海峡は渦潮で有名です。春と秋の大潮の時は潮流が早くなり、大きな渦ができるようです｡ 夏至や冬至の方が潮位差は大きくなるのですが、大きな満潮から干潮までの時間が長く潮流はそれほど大きくならないからでしょうか｡ また、干潮から小さな満潮までの潮位差は小さくこちらの方の潮流は期待できないためでしょうか。１日２回規則正しく繰り返す潮流が起こる春秋の方が､ 潮流が強くなり、見応えがありそうです。
一日の潮位の変化 １日の中での潮位の変化をさらに詳しく見ていくことにします。春分秋分の大潮の頃は、１日２回規則正しく変化します｡ これに対して、夏至冬至の大潮の頃は、満潮時２回の潮位の高さは異なります。このように１日２回の潮の高さが違う現象を日潮不等といいます｡ 大潮でないときは、月と太陽の方向が違っていますから、それぞれの起潮力の大きさの合計を考える必要があります｡ それぞれの起潮力大きさは、先ほどの大潮時の起潮力の図の上側２つの間の形になります。また、太陽の起潮力は月の場合の半分ですから､ 厚みを半分にして考えないといけません。ここで、半月で小潮になっている時を考えてみることにします｡ 月の起潮力が最小になる方向と、太陽の潮汐力が年間で最大になる方向で重なったとしてみます｡ この条件のなかで、月の干潮を太陽の満潮が打ち消してしまうことがあります。この時、実際に起こって見える満潮は１回だけで､ だらだらと長い干潮が続きます。１日に１回だけしか満潮と干潮が繰り返さない事が起こります。これを１日１回潮といいます｡ ふつうの潮の満ち引きは、１日２回なので、２回潮ということになります。
満潮干潮の時刻を考える上でもう一つ注意しないといけないことがあります。例えば、瀬戸内海のような内海を考えてみます｡ 内海の出口では、外洋側の海面の高さが潮位の変化によって上下します。これに伴って、内海側の海面も強制的に上下運動をさせられることになります｡ 水面を上下運動させると、そこから波が発生し遠方に伝わっていきます。これと同じで、内海の入口で発生した海面の上下運動は､ 波の形で内海の奥まで伝わってきます。そのため、内海の奥にある地域では、干潮満潮の時刻は、内海の入り口に比べて遅れることになります｡ 実際には、奥までいって帰ってくる波や、別の入口から入ってくる波が合わさって、内海の中では複雑な波ができますので､ 単純に入口からの距離では比較できません。それでも、月が南中してから何時間後に満潮になるかは、場所毎に決まっています｡ これを利用して満潮時刻を予想することができます。
この現象は、太平洋のような大きな海でも起こっているようです。太平洋の東側で、満潮としてできた高い波は､ 太平洋を伝わってくることになります。この波は津波と同等と考えることができますから、時速８００km程度で伝わってきます｡ ところが月が南中する場所の移動速度は北緯３０度で時速１４００kmになりますので、満潮の波は遅れて伝わってくることになります｡ 日本列島の太平洋岸ではその遅れの時間は５〜６時間程度になるようです。どれくらい遅れるかは、日本近海潮浪進行図を見るとわかるのですが､ その図をネット上で見つけることができませんでした。理科年表には記載されています。ここには著作権の関係上転載できません。
潮汐が津波のような波として伝わってくるとすると、津波が大きくなるような条件の場所では、潮位差も大きくなると予想できます｡ 例えば入口が大きく奥にいけば行くほど狭まっているような入り江、入口がさほど大きくなくても深く、中に行くほど浅くなるような湾の奥では､ 干満の差が大きくなると予想できます。後者の条件に当てはまるのが九州の有明海です｡
潮汐による波は、湾の奥に入っていくと、全体の幅を狭められます。波の力は残った波に集められますので、波が大きくなります｡ また、湾が浅くなると、波の速さが遅くなるので波の後の方が前に追いつくので、波の幅(波長)が短くなります｡ このようになっても、波の前後に含まれていた力が集められて､波が大きくなります｡
河口が東側に大きく開いた大河では、潮汐の波が川をさかのぼっていくことがあるようです。この現象を海嘯(かいしょう)といいます｡
津波のことも海嘯と呼ぶ場合がありますが、最近は使い分けているようです｡
中国の銭塘江(せんとうこう)や、南米のアマゾン川のものが有名です。アマゾン川のものは現地では、ポロロッカと呼んでいます｡
他にもいくつかあるようです。このような大規模な波が発生しなくても、河口付近では川の水が上流側に逆流し､
海水が上ってくるのを確認することができます。このような川では、逆に干潮の時には川底が大きく露出することがあります(右図：肥前白石六角川)｡
このように、干潮満潮によって川の水位が高くなったり低くなったりするあたりが、川の下流域になります。再び入り江や湾の話に戻ります。奥に深く入り込んだ入り江や湾では、決まった周期の波が発生することがあります。例えば､ 洗面器に水を入れて持ってゆすってみた場合を考えてみてください。洗面器の中の水は決まった周期で行ったり来たりします｡ この現象はセイシュと呼ばれています。湾の持つセイシュの周期と潮汐の周期とが一致すれば、波が強め合うので､大きな波が発生します｡ 大きな波ができるとは、干潮満潮の差が大きくなります。カナダ東部ファンディ湾奥部のマイナス湾やアンガヴァ湾奥部のリーフ湾では､ この働きによって干満の差が１５ｍにもなります。
台風などが近づくと、満潮時の高潮に注意してくださいと報道されることがあります。満潮時は海面が高くなります｡ そこに、台風の影響でさらに海面が高くなると、防波堤を波が飛び越してきたり、海水が防波堤を乗り越え陸地が浸水したりします｡ 海面の高さは、満潮干潮だけでは決まらないようです。そのあたりを詳しく見ていくことにします。
天体の起潮力以外に海面の高さを変化させるものはいくつかあります。先ほど述べました、セイシュもその一つです｡ 大阪湾では、平均の水深を５０ｍとすると、波が端から端までを往復するのに、いちばん長い距離だと１時間半ほど､ 短い距離だとその半分の時間かかります。従って、大阪湾の岸では１時間程度の周期で海面はわずかに上下運動を繰り返していることになります。
太平洋岸の地域では黒潮の影響が現れることがあります。黒潮が陸側に接近して流れると、海面の高さは高く、陸から離れると低くなります｡ これは、北太平洋を黒潮が回るコースの内側では海面が高くなっているためです。
台風の時には、２つの効果によって海面が高くなります。一つは気圧が低くなるために海水面が吸い上げられる現象(吸い上げ効果)で､ もう一つは、風によって海水が流されてくる現象(吹き寄せ効果)です。吸い上げ効果は､ ストローでジュースを飲むときのことを考えるとわかります｡ ストローで吸うことによって、ストローの中の気圧が下がるため、ストロー内部のジュースの液面が上がっていきます｡ ここで台風の周りを囲むストローの巨大な太さの筒があると考えてみてください。台風の中心が空気を吸い出します｡ すると海面が上がっていきます。簡単な計算から(気圧が約１０００hＰaから０になると１０ｍ上昇する) １hＰa気圧が下がると海面は１cm高くなります。９６０hＰaの台風だと５０cm海面が高くなっています｡ もう一つの吹き寄せ効果は、風と海水の関係によって起こる現象です。熱いスープを飲むときを思い浮かべてください｡ 息を吹きかけて冷まそうとすると、息の勢いに押されてスープが向こう側に流され、液面の高さは手前側が低くなり向こう側が盛り上がります｡ これと同じで、入り江に沿って風が吹き続けると、海水が風に押され、風下側に流されていきます。そのため､ 入り江の風上側で水位が低く、風下側で水位が高くなります。冬の間、日本列島には北西の季節風が吹き続けます。太平洋岸では､ 沖合に向かって風が吹き続けることになり、潮位が低くなる傾向があります。
このように潮位は、月や太陽の起潮力によってほとんどが決まりますが、海流や気象の状態によっても多少変化します｡ 月や太陽の起潮力によって起こる潮汐を天文潮、気象や海流によって起こる部分を気象潮と分けて考えることができます｡ 気象庁や海上保安庁あるいはそのデータを利用して発表される潮位の予測は天文潮によって起こる部分を予測したものです。
潮汐は、潮の流れを生みます。それによって、土砂などが運ばれ堆積し、独特の堆積物を作ります。一般的には､ 満ち引きの流れによって、粗い堆積物が流されてきたたまり、満潮干潮の時には流れが止まるため細かい堆積物がたまります｡
右写真は、大阪府寝屋川市にあった崖に見られた地層の断面です。今から５０万年前の大阪層群と呼ばれる地層のものです。
海底に堆積したと考えられている海成粘土層の最上部の部分になります。色の青っぽいところは粘土で、茶色から白っぽい色のところは､
極細粒から細粒の砂でできています。海成粘土層は平穏時に、泥の成分がゆっくりと沈殿してできたものです｡
これに対して砂層は、洪水時に泥水となって運ばれてきた砂が堆積してできたものです。真ん中あたりにある砂層に注目すると､
薄い粘土層を挟んでいます。これは、洪水の流れが速くなったり止まったりしていることを示しています｡
このようなことが起こるのは、洪水の流れを満ち潮の勢いが押し返し、流れを止めてしまったためにできたと考えられます｡
洪水が発生し、治まるまでの数日の間、潮汐の勢いによって流れが強くなったり弱くなったりしていたことがわかります。一般に、潮汐の堆積物とされているのは、ヘリンボーン斜交葉理です｡ 斜交葉理の作るハッチ模様が、右向き左向きと交互に積み重なっているものをいいます。斜交葉理の傾きの方向は、流れの方向を示していますから､ 流れが、右向き・左向きと交互に変えていたことを示しています。流れの変化は、満ち潮・引き潮の時に起こり､ これが原因でハッチ模様の向きが変わったと推定できます｡
向きの違うハッチ模様を上下に重ねてできる模様をヘリンボーン模様といいます。これは魚(ニシン=herring)の背骨 (=born)の向きが上下で逆であり、それに似ていることから来ています。ヘリンボーン斜交葉理は、ヘリンボーン模様を持つ斜交葉理という意味で､ ニシンの背骨に似ているから名付けられたという説明は誤りと思えます。
堆積物から潮流の強さが周期的に変わったことがわかれば、潮の満ち引きがあったことを示します｡
これ以外でも、潮の満ち引きがあったと考えられるものが報告されています。貝殻にある成長線を使って、その貝の年齢を読み取ることができます。寒さに弱い貝は冬になると活動が停止します｡ その時期は、貝殻の成長が悪くなるため、貝殻に筋ができるのです。同じようなことが、１日の中でも起こることがあります｡ 干潟に棲息する貝では、干潮時には周りに海水がなくなれば、活動が停止します。この時にも筋が狭い間隔でできます｡ 千葉県で発見される１４万年前のヌマコダキガイの化石には、このようなパターンが見られるものがあるようです｡ パターンを解析してみると、周期的に間隔が開いたり狭まったりしている様子が読み取れ、大潮・小潮の変化を示しているように見えます｡ このような模様は、他の貝にも見られるのでしょうか。右写真はアサリのものです。ほぼ１年間と見られる部分を拡大しています｡ その間に２０本ほどの筋が確認できます。これは、大潮小潮の繰り返しを表しているように見えます｡ 実際には、砂浜海岸では、沖合から海底砂丘のようなものが沖合から周期的に移動してくることがあります｡ この影響で、海底が浅くなったり深くなったりします。また、砂をかぶることによって貝の成長に影響があることも考えられます｡ 年輪と思われる縞の近くでは、成長停止期の影響を残しているので、細かい縞がたくさんできるはずですが写真からは読み取ることができません｡ 貝の縞模様は干満や大潮・小潮といって変化だけでできるものではないのかも知れません。
同様な干満でできたと考えられる縞模様が周期的に変化し大潮・小潮の変化を示す例として報告されているものはいくつかあります｡ 南オーストラリアの６億５千万年前の地層や西オーストラリアの３０億年前の縞状鉄鉱層等にも見られるという報告があります｡ また、３億５千万年前の単体サンゴ化石からは、１(半？)朔望月周期の縞模様の変化がみられるという報告もあります。
参考文献：増田不二雄「リズミカルな地球の変動」岩波書店
３億５千万年前のサンゴ化石には、１日周期の模様がありそれが１ヶ月周期で変化していることから、干満のリズムがわかったのですが､ 同時に１年周期のリズムもあることがわかっています。ところが、この模様からわかる１年の長さは約４００日と現在より多かったと考えられます｡ 地球の公転がゆっくりしていたようにも見えます。この現象は、地球の自転が速くても起こります｡ 速度か自転速度、あるいはその両方が変化したことが考えらます。ところで、地球の公転速度を速める原因はどこにも見あたりません｡ 従って、地球の自転については、潮汐が影響を与えると考えられます。
ここで、地球と月の関係について考えてみます。地球表面で月からの起潮力が働くと地球の海面が膨らみます。単純に考えると、月が真南の空に来たとき､ 満潮になります。しかし実際には、遅れて満潮になります。これは「４章波としての潮汐」で説明したとおりです。これは、膨らんでいる方向が､ 遅れてきている事を示しています。遅れてきた海水は月の方に引っ張られて、何もない場合より速く伝わろうとします｡ 海水が、移動すると海底の間に摩擦が働きますので、地球の自転もその影響を受けることになります。月の公転は地球の自転より遅いので､ 月の公転に引かれるように地球の自転は遅くなっていきます。このように公転の潮汐力により自転速度を弱める力を潮汐摩擦といいます｡
地球の自転は潮汐摩擦によって、次第に遅くなっています。いったいどこまで遅くなるのでしょうか。単純に考えて見て､ 地球の自転と月の公転が同じになれば、潮汐摩擦は働かなくなります。この時には、自転速度は影響を受けなくなり変化がなくなります｡ つまり、地球の自転と月の公転が同じ速さになるまで、地球の自転が遅くなります。このようになれば、地表から見ると月の方向は､ 決まった方向になります。地球の片側では、月はいつも同じ方向に見えるのに対して、反対側では全く見られない事になります｡ 小さく暗くてみることはできませんが、地表から見る静止衛星ような関係になります。
月は公転周期と自転周期が全く同じです。そのため、地球から見ると月はいつも同じ面しか見ることができません。月から地球を見たとすると､ 月の表側からは、地球がいつも同じ位置に見えるのに対して、裏側からは地球を見ることはできません。このようになったのは､ 地球の起潮力が月に働いたからといわれています。起潮力は質量に比例しますから、月の８０倍もの質量を持つ地球が月に及ぼす起潮力は､ 月が地球に及ぼすものに比べて２０倍にもなります(月の半径が小さい分だけ小さくなっています)。この強大な起潮力によって､ 月の自転にブレーキがかかり、かなり早い時期に自転周期と公転周期が一致するようになったと考えられます。太陽系全体を見渡してみると､ 月のように自転周期と公転周期が同じものは、木星のガリレオ衛星をはじめ多数あります。
月には、海水がありません。そのため潮の満ち引きがないはずです。それなのに潮汐摩擦が働き自転にブレーキがかかるというのはなぜでしょう｡ 実は、地球では海水が満ち引きを繰り返しているだけではなく、岩石でできた硬い地球自身も膨らんだり縮んだりを繰り返しています｡ 地面の長さを精密に測ることのできる器械を利用して、地面の伸び縮みの様子を測定してみると､ 海水の潮汐と似たリズムで変化していることがわかります。壁紙となっているグラフは､ 名古屋大学地殻変動研究所で地面の長さを測定した記録です。このように固い地球自体も月や太陽の引力で変形しています｡ この変形を地球潮汐といいます。
月の潮汐摩擦によって地球の自転はだんだん遅くなっています。それでは、自転運動が持っていたエネルギーはどうなったのでしょうか｡ 自転と互いに作用しあっているものは、月の公転ですので、月の公転にエネルギーが使われることになります｡ この場合、公転速度を上げるより、軌道を持ち上げるのに使われます。ケプラーの第３法則※の関係から､ 軌道が高くなると公転周期が長くなります(エネルギーをもらっているのに遅くなるのは変な感じがしますが、この通りです)｡ 地球の自転も月の公転も遅くなります。最終的にはどちらも現在の４０日くらいの長さになるようです。
地球によって月に働く起潮力の大きさは、月によって地球に働く起潮力に比べると、月が小さい分弱くなりますが、それ以上に地球の質量の影響を受け､ 大きくなります。月の半径で４分の１倍、地球の質量で約８０倍なので、実質２０倍になります。これほど大きな起潮力が月の自転に影響したようです｡ 起潮力公式参照
ところで、起潮力の大きさが重力の大きさより大きくなるとどうなるのでしょうか。等しい時点で無重力ということになります｡ さらに起潮力が大きくなれば、相手の天体に表面の物質が引き寄せられることになります。簡単に言えば、そうなった天体は破壊されてしまいます｡ 月の場合ではどれくらいの距離になるのでしょうか。月の表面重力は地球(約１０Ｎ)の約６分の１で約１．７Ｎ、月表面での起潮力は､ 地球の表面の起潮力(１.１×１０−６)の２０倍の２.２×１０−５。これは表面重力の１.３×１０−５倍になります｡ 起潮力は距離の３乗に反比例しますので３乗根をとった２.４×１０−２倍の距離に近づいたときになります｡ これに月までの距離(３８万km)をかけた、８９００kmという値が、月の破壊が始まる距離になります。これは上空８００kmの高さ (地球の半径、月の半径を減じた値)にまで月の表面が接近した時にあたります。実際には、月は起潮力によって伸ばされ､ その分だけさらに起潮力が大きく、重力が小さくなりますので破壊はもっと遠くで起こることになります｡ このような破壊が起こる上限の高さのことをロシュの限界といいます。こうしてみると、大きな小惑星などが地球に衝突しようとした場合､ 衝突直前に小惑星が破壊されることになります。実際、木星や土星にある輪は、落下してきた衛星が破壊して出来たと考えられています。
起潮力が大きな天体とは何があるでしょうか。質量が大きく、中心からの距離が近いほど起潮力が大きくなります｡ 半径がちいさくないと近づくとはできません。このように考えてみると、起潮力が極端に大きな天体としてブラックホールがあげられます｡ ブラックホールに近づくにつれ、その起潮力によって物質は引き裂かれるばかりでなく、分子や原子までもバラバラにされてしまうことがおるそうです｡ 最終的には素粒子レベルまで破壊されるようです。起潮力だって大変なことを起こすことが出来るようです。
※ケプラーの第3法則 ケプラーが発見した惑星の軌道運動についての法則の３番目のもの｡ 調和の法則ともいう。内容は公転周期の２乗と公転半径の３乗は比例するというもの。公転周期は公転半径の１．５乗に比例することになる｡ この法則は、引力で周りあっているものに適用できる。
○補足
遠心力を使った起潮力の説明に見られる間違い
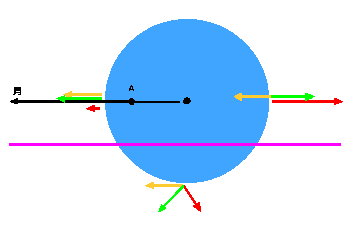遠心力を使って起潮力を説明しているものは、要約すると次のようになります(右図)｡／／月は、地球を中心にまわっているのではなく、月と地球の共通重心を中心にして回っている。同時に地球も共通重心を中心に公転している｡ 共通重心は地球の中にある(図中Ａ)。地表では遠心力が共通重心から外側に向かって働く｡ 地表の月に向いている場所では、月の引力(黄色矢印)と遠心力(赤色矢印)は月の方に向かって働く｡ その合力である起潮力(緑色矢印)は月の方に向かって働く。月と反対側の場所では、遠心力は月と反対の方向に働き、引力よりも大きい｡ 二つの力の合力である起潮力は月と反対側に働く事になる。／／
補足：地球の中心では月の引力は地球公転の向心力として働くので、引力と遠心力の大きさは等しくります｡ 共通重心を中心とする回転運動では、距離が長い分だけ遠心力は引力より大きくなります。
この説明が誤りであることは、干潮が説明できないことから明らかです。この時の図は書かれていないことが多いので､ 桃色線より下に示しておきます。遠心力を共通重心から外側に引くと、引力を打ち消す方向には働かないことがわかります｡ 計算はしていないのですが、月の引力に匹敵する大きな起潮力が外側に向かって発生していることは簡単に想像できます。
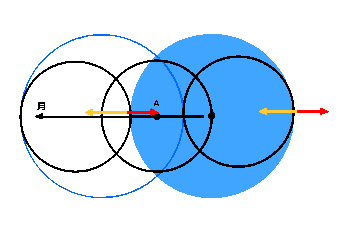それでは、この考えのどこに誤りがあるのでしょうか。それは、地表の一地点の公転運動のしかたについての考えにあります｡
地球は自転していないものとして考えてみます(右図)。月が半分だけ公転した時(半月後)は、どうなっているのでしょうか｡
半月後の地球の位置は、青輪郭線だけで示しています。左側(月のある側)にあった地点は、自転しないので半月後も地球の左側にあります｡
この地点が公転することによって移動する経路は、もとあった位置と半月後の位置を直径とする円上に乗ってきます(左側黒線の円)｡
この時の遠心力は、この円に対して働きますので、右向きになります。同じように、右側(月と反対側)の動きも考えてみることにします｡
半月後の位置とで直径になる円を描いてみると右側の黒線円になります。円の直径は左側の円と同じです｡
この場所での遠心力も、ここで書かれた円に対して働きますので右向きになります。円の大きさも同じなので大きさも同じです｡それでは、起潮力はどのようになるのでしょうか。起潮力として影響を与えるものは遠心力と月の引力の２つになります｡ ここで遠心力の大きさに注目してみます。先ほどの図で地球中心の動きも考えてみることにします｡ この円は、地球の動きを表していますから、当然、共通重心を中心とする円運動になります(下段真ん中の黒線円)｡ この線上での運動では、月からの引力と回転による遠心力は釣り合っていますから、それらは同じ大きさで互いに逆向きになります｡ 図に書かれた黒線円３つから、地表の一地点の回転運動の半径や周期は、地球の中心の回転運動の半径周期と同じになる事がわかります｡ 従って、遠心力はどこでも、地球中心に働く月からの引力と同じ大きさで反対向きで働いていることがわかります｡ 地表上月側の地点での起潮力は、月からの引力と遠心力の合力です。遠心力を月からの引力と置き換えて表すと、起潮力の大きさは､ 月からの引力と地球の中心に働く月からに引力との差になります。このことは、地表月から反対側の地点でもいえます｡ 説明が回りくどくなっていますが、最終的には、起潮力の原因については、本文中の説明と同じ結論に達します。
上段の図の起潮力では、地球を共通重心の周りを公転させる時に、同時に地球を自転させてしまっているのが間違いの元となっています｡ そのため、起潮力よりはるかに大きな地球自転の遠心力が加わり、それを地球裏側で起こる満潮の原因にしてしまったようです。
調べてわからなかったこと(その１)潮汐のリズムの現れ方について
起潮力の大きさが、そのまま海水面の高さとなると仮定して、潮汐の変化がどのようになるかを考えてみることにします｡
起潮力によって海面の高さが変化する様子は、少し傾けたラグビーボールを緯度に相当する高さで切ったときの断面の形で表すことが出来ます｡
(前述)地球に起潮力を及ぼすものは、月と太陽の２つが主なもので、２つの力の合計が地球に働いている起潮力になります｡ ここで、夏至冬至前後で小潮になった頃を考えてみます。太陽の起潮力は右図右上に示しています。夏至の頃の太陽は図の上の方向にあります (冬至では下)。この頃太陽は赤道面から２３.４度離れた方向にありますので、起潮力で出来る楕円の中心は地球の中心とずれます｡ 小潮の時は半月ですので、月は太陽と９０度離れた方向にあります。図では横の方向になります。このとき月は赤道面上にいることになります｡ 月の起潮力が描く楕円の中心は地球の中心と一致します。また、月の起潮力は太陽の２倍ですから、楕円のふくらみも２倍になります｡ この様子を表したのが右図左上です。太陽と月の起潮力の合計は右図下のようになります。夏至の頃で考えてみると、 図の上が正午、左が夕方、下が夜中、右が朝方(冬至では下が正午)になります。水色の部分の幅がが潮位の高さを表していますから､ 夜中に潮位が最も低くなり、それ以外は一日中潮位が高い状態が続くと考えられます(１日１回潮)。
同様に夏至・冬至前後の大潮の時を考えてみます(左図上)。このときは赤線で示した太陽の起潮力の方向と､
黄線で示した月による起潮力の方向が重なります。両方の合わさった起潮力はそのまま大きくした形になります。夏至の日でいえば､
昼間に大きな満潮、朝夕に干潮、夜中に小さな満潮が起こることになります。春分・秋分前後の小潮の時はどうでしょうか(左図下)。太陽は赤道面上にあるので、潮汐の中心は地球の中心と一致します｡ 月は太陽から９０度離れていますので、赤道面から２３.４度離れることになります。従って、潮汐の楕円は横向きになり､ 夏至点側にずれることになります。両方の合わさった図形は、夏至点側にだけふくらんだ形になります｡秋分の日の潮位で見ると､ 明け方(春分では夕方)に満潮になり、それ以外は潮位の低い状態が続きます。
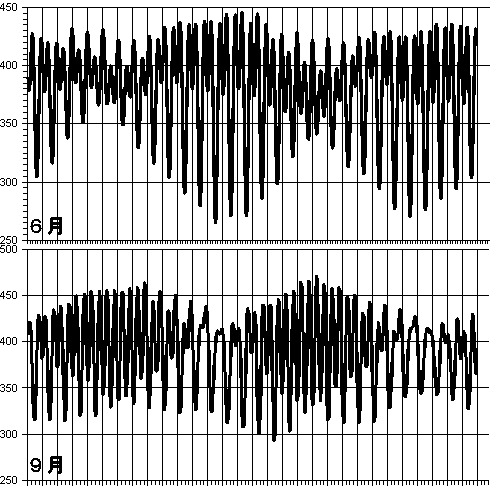ところで、実際の潮位はどうなっているのでしょうか。２００９年６月と９月石廊崎の潮位の変化を右に示します
(データは気象庁のホームページより入手)｡
６月は、５日と２０日頃に小潮になっています。夜中に満潮になり、その後潮がわずかに引いた状態で上下しています｡
また、１３日と２７日頃大潮になります。昼に干潮になり、それ以外は潮が高い状態で上下しています｡
９月は１３日と２７日頃が小潮で、朝方に干潮になった後、満潮が続く典型的な１日１回潮になっています｡
理論的に考えられる起潮力のリズムと、潮の高さのリズムを比べてみると、潮の動きが全く逆になっているように見えます｡
観測される潮汐のリズムは、本州四国九州の南岸で共通してみられます。これは偶然の一致というより何か理由があるようにも見えます｡
これらの地域では、満潮干潮が、月の動きより６時間遅れているといわれています｡
そう考えれば、満潮が起こるはず時刻に干潮が､干潮の起こるはずの時刻に満潮になることが理解できます｡
詳しく見てみると、そうとも言い切れないようです。小笠原や琉球の孤島の潮位の変化を見ると、全くでたらめになっています。実際に太平洋を伝ってきた波が､ さまざまに干渉しあっているためなのですが、ここまで規則性が見られると何か理由があるようにも見えます。
調べてわからなかったこと(その２)起潮力による盛上り量について
起潮力の大きさは式で表すことが出来ます。その力に引かれて海面がふくらむとするとどれくらいの量になるか計算で求められるはずです｡ そこで、月だけによる起潮力の大きさを実際に求めてみることにします。方法は２通り考えられます。それぞれの方法を説明します。
位置エネルギーの大きさを利用する方法 海面の高さでは、位置エネルギーが等しくなっています。もし違っていれば､ 海水は、位置エネルギーの小さい方に向かって流れていき、最終的に位置エネルギーが等しくなるように変化します｡ 今ここで、地球の中心からｒの所での地球の重力加速度の大きさをＧ(ｒ)とします。また、起潮力は公式から､ ｋ×ｒと表すことができます｡ Ｆの力が加わっているところでｓ持ち上げたとき位置エネルギーはＦｓ大きくなります。月と直角方向で地球の中心からｒ離れた場所で､ ｄｒだけ持ち上げるとＦｄｒだけ位置エネルギーが大きくなります。従って地球の中心の位置エネルギーを０としたとき､ 質量ｍの物体の地表での位置エネルギーは(地球半径をＲとする)、中心から半径Ｒまでの間で積分して
╭Ｒ | ｍＧ(ｒ)ｄｒ ╯０ また、月方向の地表面での位置エネルギーは、 ╭Ｒ ╭Ｒ １ Ｒ | ｍ｛Ｇ(ｒ)−ｋｒ｝ｄｒ＝| ｍＧ(ｒ)ｄｒ−[−ｋｒ２] ╯０ ╯０ ２ ０ ╭Ｒ １ ＝| ｍＧ(ｒ)ｄｒ− −ｋｍＲ２ ╯０ ２ 両者の差が位置エネルギーの差になるので引き算して １ −ｋｍＲ２ ＝ ｍｇｈ(位置エネルギーを求める公式) ２ ｋＲ２ → ｈ＝-------- …………(１) ２ｇ
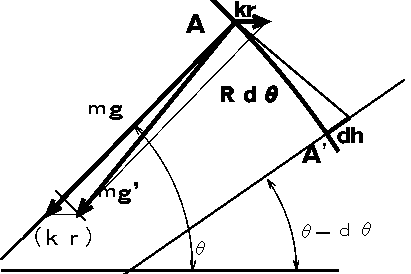右図で、右方向に月があります。Ａ地点から微小中心角ｄθだけ月側によったＡ’地点で海面が持ち上がる量ｄｈを求めてみます｡
図でｇは、起潮力がないとしたときの重力加速度の大きさと方向、ｇ’は起潮力も働いたときの重力加速度の大きさと方向です｡
この矢印の先は、起潮力の大きさｋｒだけずれています。ｄθが非常に小さいときＡＡ’とｇの方向は直角になります｡
また、ＡとＡ’からｄｈ外側を結ぶ線は海面ではｇ’に対して直角になります。従って、Ａからｄｈを望む角と、ｇ−ｇ'
のなす角は等しくなります。対応する三角形の関係から、次の式を作ることが出来ます。Ａ−Ａ’：ｄｈ ＝ ｇ −ｋｒcosθ：ｋｒsin θ
ここで Ａ−Ａ’＝ Ｒｄθ、ｒ＝Ｒ cosθ であり、ｇに比べてｋｒが非常に小さく ｇ − ｋｒ cosθ ＝ ｇ とできるから
Ｒ ｄθ・ｋＲ cosθ・sin θ ｄｈ ＝ --------------------------- ｇ ｋＲ２sin 2θ・ｄθ ＝ -------------------- ２ｇ中心角π／２から０までの間で積分して全体のもり上がり量を求める
╭０ ｋＲ２sin 2θ ｋＲ２ ０ | ---------------ｄθ ＝ -------［ cos ２θ］ ╯π/２ ｇ ｇ π/２ ｋＲ２ ＝ --------- ……(２) ２ｇ
遠心力の式で、ωは角速度なので、２４時間(正確には２３時間５６分)で自転している地球の場合 ２π÷（２４時間×６０分×６０秒）から､ ０.００００７３(rad/s)になります。
地球の扁平率はｈ／Ｒなので、(１)または(２)式の結果をＲで割って
ｋＲ／２ｇ ＝ ω２Ｒ／２ｇ ＝（７.３×１０−５)２×６.４×１０６／(２×９.８)
計算結果は１.７×１０−３となり、実際の扁平率の値３.４×１０−３に比べて半分しかありません。
結果が異なるのは、式に何らかの誤りがあるためだと考えられます｡ 式の作り方のどこに問題があるのかよくわかっていません。そのため、起潮力によって海面がどれくらい持ち上がるのか､ 結論を出すまでには至っていません。
「潮の満ち引き」という用語について
一般的には、「満ち干」といわれているようなのですが、これは「潮が満ちる」の「満ち」と「干潮」の「干」をあわせたものだと思われます｡ このときに「満ち」は潮の変化の様子を表しているのに対して、「干」は潮の状態というように異なった現象を表しています｡ これはものすごくちぐはぐな感じがします。「潮が満ちる」または「満ち潮」に対して、「潮が引く」「引き潮」という言葉がありますので､ 熟語としてはそのまま組み合わせた「満ち引き」という方が現象をよく表していると感じられます(｢干｣を使いたいのなら「干満」がある)｡ こういった理由で、この章のタイトルは「満ち干」ではなく「満ち引き」ということにしています。
ヨッシンと地学の散歩 ＜道標(top)＞