−−振り子を使って重力加速度を求められるか−−

　重力加速度の大きさを求める方法として、振り子の振れる周期を利用できると教科書等に書かれています。振り子の振れる周期は、 重力加速度の平方根に反比例するためです。ただし、この性質は、振り子の振れ幅がじゅうぶんに小さい場合という条件がつけられています。 それでは、どれだけ小さいと正しく結果が求められるのでしょうか。検証してみます。

　まず、計算式の根拠と実際の計算式を考えてみます。重要と思われるものは７式あります。 次にあげておきます。消化しきれていないところもありますので、 だいたいの感じで説明します。振り子のひもの重さ、空気の抵抗等による減衰は無視できるものとします。 これは実験の方法を工夫することで解決できるものとします。
　次に記号を定義します。振り子の支点からおもりの中心までの長さをＬ、 振り子の振り角をθ、最大振り角をθ_０、おもりの質量をｍ、おもりは球形で半径をｒ、重力加速度をｇとします。
　順番に式の意味を説明します。

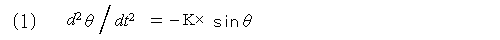
　振り子のおもりにかかる重力のうち、ひもに対して直角方向成分(ｍｇ sinθ)は、振り子を支点として回転させる加速度として加わります。 この式が振り子の運動を表す一般式です。この中で、Ｋ≡(ｇ/Ｌ)/(１＋０.４ｒ^２/Ｌ^２)としています。おもりの半径が非常に小さいときは Ｋ≒ｇ/Ｌと近似することができます。ただし、ｒ：Ｌ＝１：１００の場合でも、有効数字６桁目に影響してきますので、近似する場合注意が必要です。


　(1)式で振り角θが非常に小さいときには、sinθ＝θとなることを利用した近似式です。この式は、単振動を表す公式と同じです。


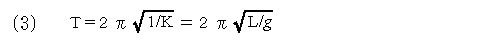
　(2)式から求めた、周期です。この式が一般的に使われている振り子の周期を求める公式になります。ｒ＝０としています(以下同様)


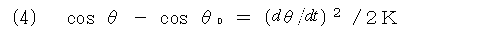
　振り子の運動を表すもう一つの式です。力学的エネルギー保存の法則を利用しています。左辺は位置エネルギー、 右辺は振り子の回転エネルギーを表しています。


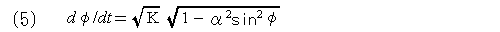
　(4)式をα≡sin(θ₀/2)、sin(φ)≡sin(θ/2)/αの関係になるαとφを使って変形させたものです。 この形の微分方程式は第一種完全楕円積分といって解が求められています。


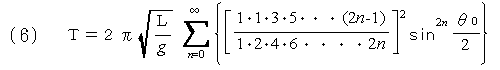
　(5)式を級数(テーラー)展開を利用して周期を求めたものです。Ｋは近似式の値を使っています(以下同様です)


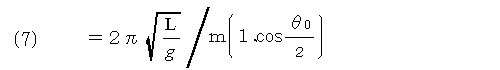
　(6)式はさらにここまで変形できるそうです。ここで使われている関数ｍ(Ａ，Ｂ)は２数Ａ,Ｂの相加相乗平均の極限値(算術幾何平均)のことです。 ＡとＢの相加平均と相乗平均を計算し、さらにその結果の値を使って相加平均相乗平均を計算しということを、 両者が一致するまで繰り返して求められた値を表しています。

　計算式ができたところで、式を使って周期を求めることにします。(6)(7)式のどちらを使えばよいかを考えてみます。 有効数字１２桁で計算するとき、(6)式では第１０項まで計算する必要があるのに対して、(7)式では３回目くらいで収束します。 従って(7)式の方が計算が楽なのでこちらを使用することにします。
　回転半径１ｍの振り子を重力加速度９８０cm/s^２(ガル)の場所で振ったときの振り角の大きさと周期、その周期から (3)式を使って求められる重力加速度の大きさを表計算ソフトで計算すると次の表のようになりました。(有効数字１２桁です)

角度	周期(秒)	重力加速度(ガル)	誤差(％)
０	2.00708992315	980.000000000	0.0000000
５	2.00804564415	979.067368123	-0.0009517
１０	2.01091782126	976.272577969	-0.0038035
２０	2.02248234754	965.139871175	-0.0151634
３０	2.04203094538	946.749530292	-0.0339291
４０	2.06999316329	921.344217628	-0.0598528
５０	2.10700880176	889.256476937	-0.0925954
６０	2.15397279226	850.901541125	-0.1317331
７０	2.21210394199	806.768025143	-0.1767673
８０	2.28304985468	757.406357649	-0.2271364
９０	2.36904972217	703.414610826	-0.2822300

　５度の振り角では、１ｍのひもの長さの時、振れ幅は９cmになります。この時すでに、 おもりを直径１０cmの質点と考えたときに生じる誤差以上の誤差が発生しているのがわかります。さらに１０度では、 １０回程度の時間の読み取りから発生する誤差と同じくらいの計算誤差が発生しています。学校実験では２０度以上の振り角で測定していることを考えると、 実験誤差以上に計算式から発生する誤差があることがわかります。 場合によっては９００ガル以下という結果が出ても当然だということもありえます。 計算式の使い方に注意が必要なことがわかります。

---

−−参考にしたのは、以下の資料です−− ウェブサイト｢物理のかぎしっぽ｣(http://hooktail.sub.jp/mathInPhys/elliptical/)
天体力学入門講座(９)　井上猛　天界　２００５年１１月号