ヨッシンと 地学の散歩
散歩道の四方山話
散歩道の四方山話
言葉がにているためか、よくどっちだったかわからなくなることがありますが、太陽が見えなくなる現象が｢日食｣､ 月が見えなくなる現象が「月食」です。太陽・月の一部分が見えなくなるのが、部分日食・部分月食､ 全体が見えなくなれば、皆既日食・皆既月食です。日食の場合、真ん中が丸く見えなくことがあり、これを金環日食といいます。
見えなくなる原因は、日食と月食の場合で異なります。これがわかりにくくしている原因と思われます｡ 日食は太陽の手前側に月が割り込みじゃまをして見えなくなる現象で､ 月食は地球が作る影の中に月が入ることによって見えなくなる現象です。天文学用語では、前に割り込んで見えなくなる現象は ｢掩蔽(えんぺい)｣、影の中に入ることで見えなくなる現象は｢(影による)食｣とよんでいます。実際には｢食｣ といった場合この両方をあわせて言うことが多いようです。
もう少し詳しく見ていくことにします。
内 容
１．日食の起こり方
２．月食の起こり方
３．新月・満月の度に日食・月食が起こらないわけ
４．日食・月食は毎年同じ時期に起こるか
５．日食と月食の頻度
６．日食・月食は予報できるか
７．天体の食・掩蔽現象
８．日食・月食の用語
２．月食の起こり方
３．新月・満月の度に日食・月食が起こらないわけ
４．日食・月食は毎年同じ時期に起こるか
５．日食と月食の頻度
６．日食・月食は予報できるか
７．天体の食・掩蔽現象
８．日食・月食の用語
１．日食の起こり方
日食が起こる場合を考えてみます(下図、太陽・月・地球の大きさはでたらめです)。月が地球と太陽の間に割り込むわけですから､ 太陽−月−地球はこの順番で一直線に並んでいます。また、地球から見て月は太陽の光が当たっていない面が見えるわけですから､ 月は新月になっています。日食は新月の時に起こる現象です。
)。本影錐の中では、太陽が完全に月に隠される事を確認してみます。地球上
(水色)で本影錐の中の点、例えばＡ点で考えてみます。Ａ点から月の両端を結ぶ線が月の大きさになります｡
太陽との大きさを比べるために太陽の位置まで引っ張っていきます。この時にできた暗黄色のＡ'
の円と位置が太陽と比較した月の位置と大きさになります。明らかに太陽の赤丸を覆っているのがわかります。この状態が皆既日食です。
<部分日食> 次に、太陽の下端と月の上端というように反対側どうしを結ぶ線を考えてみます｡ 太陽と月の間の一点を頂点とする円錐型の図形がかけます(図中月地球間では明るい灰色の部分)。この円錐形を｢半影錐｣といいます｡ どうしてそういう名前になっているか考えてみます。半影錐内の地表の一点Ｂ点に注目します。先ほどと同じようにして書いてみると､ 太陽と月の大きさ・位置の関係は図中Ｂ'の円となります。この円は太陽の一部分だけ隠しています。この状態が｢部分日食｣です｡ 太陽の一部分がが隠れ、半分だけ影になっている状態なので｢半影｣錐と呼ばれます。半影錐の縁ではここと月太陽を結ぶ線が直線上に並びます｡ これは太陽と月が横にくっついて見える事を示しています。これより外側では太陽と月は離れて見えます｡ 半影錐の内側が部分日食の見える場所といえます。
<金環日食、金環・皆既日食> 上の図では、本影錐が頂点までできないうちに地球が割り込んできました｡ 頂点まで書けばどうなるのでしょうか。書いてみました(下図)。
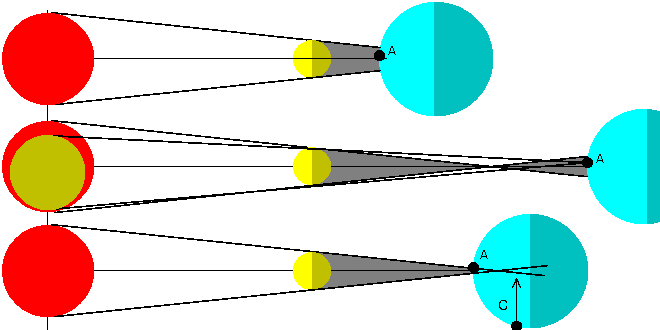
ところで３番目の図のような場合どうなるのでしょうか。Ａ点は本影錐の頂点より手前側にありますので皆既日食を見ることができます｡ Ｃ点は今は本影錐の中にありませんが、地球が月が作る影の中を横切っていきますので、本影錐の中に入っていきます｡ その位置は頂点より先になりますので、金環日食が見られる事になります。Ｃ点の時刻は､ 自転によって薄水色の部分に入る直前なので夕方になります。明け方にも金環日食が見えていた場所があります。Ａ点は正午頃となります｡ 同じ日食でも場所(時刻)によって皆既日食・金環日食と違う場合があります。このような日食を｢金環皆既日食(ハイブリッド日食)｣ といいます。金環日食から皆既日食に変わる場所では、月の縁にある高い部分がさえぎられ、とぎれとぎれの環が見られます。
金環日食や皆既日食が起こったりするのは、まず第一に月や太陽の見かけの大きさが変化しているためです。これは､ 月や太陽までの距離が変化するためです。ふつう惑星や衛星がその主星(この場合太陽や惑星)の周りを回る軌道の形は決まっていて､ その形はだ円形になります(ケプラーの第一法則)。円ではないので距離が変わる事になります｡ 実際地球から見た太陽や月の大きさは変化している様子もわかっています｡ 二番目は、地球から月までの距離(月の公転半径)が、月が作る本影錐の高さとほとんど同じであることです。短すぎても､ また長すぎてもどちらか一方にしか起こらないことになります。月までの距離はだんだん大きくなっていることが知られています (クリックすると説明文のあるところに進みます)｡ 何千万年か前は皆既日食だけが、何千万年かすると金環日食しか起こらない事になります。
２．月食の起こり方
月食の起こり方を考えるために最初の図に戻って考えてみます。図を再度載せます
上の図で、月と地球の位置を変えて考えてみることにします。今度は黄色が地球、水色が月になります。図に書かれた月は大きくなりすぎています｡ 実際にはＡ点・Ｂ点を示す黒丸の大きさくらいでしょうか。これで考えてみましょう。本影錐の中にあるＡ点の月は光が当たっていないので真っ暗です｡ これが｢皆既月食｣です。
半影錐の中にあるＢ点の月は太陽の光が当たっているので明るいのですが､ 一部地球に隠されていますのでわずかに暗くなっています。この状態が｢半影月食｣です。暗くなる割合は、本影に近づくにつれ大きくなり､ 半影錐の縁に近づくにつれ明るくなります。暗くなっていると言っても、目で見てわかるというものではありません｡ 薄雲がかかっている方が暗く見えることもあります。本影に半分かかっているときが｢部分月食｣です。皆既月食の時もそうなのですが､ 本影に入っているといっても、地球の大気中を通り抜けた赤い光が屈折して月面を照らしているので、完全の真っ黒になるのではなく､ 赤暗く光って見えます。光が通り抜ける様子を知るためには、月食中に月面近くから見た映像も参考になります。月探査機｢かぐや｣ のサイトにあります(http://www.jaxa.jp/press/2009/02/img/20090218_kaguya_2.jpg)。地球の周りから光が漏れてきているようすがわかります。
最後に月食がどのようなときに起こるか考えてみましょう。図の黒い点ではわかりにくいので、再び大きさを水色の円にまで拡大してみます｡ 黄色で書いた地球から水色で書いた月を見ると明るい面ばかりが見えています。この状態は満月です。月食は満月の時に起こる現象です。
３．新月・満月の度に日食・月食が起こらないわけ
新月や満月の時は太陽−地球−月が一直線に並んでいます。単純に考えると、満月の時には、月は地球の影に入って月食を起こし､ 新月の時には太陽を隠して日食を起こしそうです。実際には、満月といっても月食にはならないし、新月には日食が起こってはいません｡ どうしてでしょうか。簡単に答を言えば、満月の月は地球の影の上か下を横に通り抜けるし、新月の月は太陽の上か下を通り抜けるからです。
詳しく見ていきます。一般的な衛星の公転面は、母惑星の赤道面に一致していることが多いのですが、月の場合の公転面は地球の公転面 (黄道といいます)に対して約５度傾いています(天文年鑑では１９９８年版以後この記述が抜けています)｡ 月の公転面や星座の間の通り道を｢白道｣といいます。白道が黄道面に対して傾いているとどうなるか図に書いてみました。
地球がＤの位置にいるときは、新月の月は黄道面(太陽の方向)より南にいますので、月は太陽の南側を通り抜けます。これでは日食になりません｡ 満月の時も地球の影がある黄道面より上を通過します。この時も月食にはなりません。
地球がＥの位置まで進んだとします。Ｈ点は月が黄道面を南から北に横切る場所です。このような場所を｢昇交点｣といいます｡ この場所は白道上でもあるし黄道上でもある場所です。新月は昇交点にあります。黄道上(太陽の方向)にありますので、日食が起こります｡ Ｉ点を考えてみます。月が黄道面を北から南に横切っています。｢降交点｣といいます。満月は地球の影のできる黄道上にありますので､ 月食となります｡ 昇交点が太陽の方向を向くときに日食や月食が起こります。
地球がＦ点にいるときはＤ点同様日食・月食が起こりません。Ｇ点に来ると再び日食・月食が起こるようになります。降交点が太陽の方向 (昇交点が太陽と反対側)を向いたときも日食・月食が起こります。
まとめると次のようになります。日食・月食が起こるのは昇交点や降交点が太陽の方向を向くときで､ １年に２回あり、日食・月食は半月ずれてほぼ同じ頃に起こります。
４．日食・月食は毎年同じ時期に起こるか
ところで、もう一度３番目の図に戻って考えてみます。満月・新月の月の位置では、太陽からの引力の大きさがわずかに違います｡ そのために潮汐力が働きます(潮汐力についてはここを参照してください)。潮汐力は新月の時は太陽の方向､ 満月の時は太陽と反対の方向に働きます。
Ｄ点の地球・月を見てください。新月の時の潮汐力は太陽の方向です。この力は２つの力に分けて考えることができます｡ 一つは月の公転軌道を太陽の方向に引き伸ばそうとする力、もう一つは新月を黄道面に引き寄せようとする力です。前者の力は､ Ｅ点に来たときには引き伸ばそうとする方向が直角方向にずれますので、月が公転する間に打ち消しあってなくなります｡ ここで問題になるのは、後者の力です。黄道の方向に引き寄せられるのですから、月の軌道が黄道面の方向にずれます。昇交点の位置もずれ､ 予定よりの手前側になります。
昇交点通過後満月に達するまでは、潮汐力は太陽と反対向きに働き、月を黄道面に引き寄せる力として働きます。その結果､ 昇交点に達するまでと逆順の動きで満月になります。新月−昇交点が短かったのと同様に昇交点−満月間の距離が短くなります｡ 満月の位置も予定より手前側になります。同様に降交点、新月の位置も手前側になります。
(文章では、新月・満月と書いていますが、正しくは昇交点・降交点の中間地点のことで､ 月が軌道上で最も南や北にずれる地点のことをいっています)
全体としてみると、月の公転面の傾きの方向が手前側に回転していきます。これは黄道を北側(上)から見ると右回り(西回り) にまわる方向です｡ 昇交点の方向(昇交点黄径といいます)も西回りにまわっていきます。
ＥやＧの位置では、新月・満月が黄道面上にあるため黄道方向に引き寄せる力はなく、新月の時には潮汐力が働かないため､ 月の公転面の傾きの方向を回転させません。Ｆの位置ではＤと同様、月の公転面の傾きの方向を西回りに回転させます。
ちょっとわかりにくいので、違う考え方をしてみます。月の公転を、黄道面に沿う運動と垂直な方向の運動に分けて考えてみます｡ 太陽の影響がない場合、月の運動は地球の引力だけで決まりますので、黄道面に沿う運動と垂直な方向の運動の周期は同じです｡ でなければ一周すると同じ所に帰ってきません。ところがＤ点にいるときは、黄道面に垂直な方向の運動には、太陽の潮汐力が加わるので､ その分だけ地球の引力が強くなったように振る舞います。引力が強くなるとその分だけ回転が速くなります (実際には上下往復運動なので振り子の振れ方ににます)。回転が速いと周期が短くなります｡ 黄道に沿う運動では、太陽の影響を受けませんので、周期は変わりません。結局１周する前に、昇交点・降交点に戻ってしまいます｡ 周期が少なくなる分だけ、昇交点・降交点が手前側(西側)へ移動します。
１年の間では、公転面の傾きの方向(昇交点黄径)が西回りに回転します。西回りに回転した昇交点の延長が太陽を指すのは図ではＥ点の手前になります｡ １年に達する前に日食月食の起こりやすい時期がやってくることになります。そのため２０１１年のように、１・６･ １２月と年に３回も月食が起こるという年ができます。
昇交点の方向が太陽を指してから、再び同じになるまでを｢１食年｣と言います。１食年の長さは３４６.６２０１日で､ １年より約１９日短くなっています。日食月食の起こる時期は毎年２０日ずつ早くなります。
<参考文献>戸田盛和著「コマの科学」岩波新書 １９８０年
５．日食と月食の頻度
どちらがよく起こるかは、日食が起こるときの月の位置と月食が起こるときの月の位置を比べ、どちらが広いか考えればわかります｡ 図は少し正確にしましょう。地球の大きさは月の大きさの約４倍です。月が作る本影錐の頂点は､ 地球上で皆既日食が見えたり金環日食が見えたりするので変化しますが、ほぼ、地球上に来ると考えます。図を書いてみました(下図)。
左側１から３の番号をつけた月に注目します。太陽側にありますので、日食を起こす月です。３番の月は､ 球の中心に本影錐があたるように書いています。１番の月は、半影錐の端っこが地球にかかろうとしています。もう少しだけ地球側(３番側) によれば、北極か南極で部分日食が見られることになります。この位置が部分日食が起こる境界になります。３番からの月の中心の位置のずれは､ 月の３個分の大きさ、約１.５度になります。２番の位置よりほんのわずかだけ地球側によれば、本影錐が地球にかかります｡ どこかで皆既日食が見られることになります。実際には、地球の位置がこれより月に近かったり遠かったりしますので､ 地球上に本影錐が落ちていることになり、２番の位置でもじゅうぶんに皆既日食や金環日食が観察できます。この位置は３番の位置から月２個分､ 角度で１度離れています。
今度は右側４番から６番の番号をつけた月に注目します。６番の月は完全に本影に入っていますから、皆既月食になっています｡ ３個並んでいますので、月の中心が本影錐の中心から月１個分(０.５度)以内にいる必要があります。５番の月は本影に接しています｡ ほんの少しだけ本影側によれば部分月食になりますので、部分月食を起こす境界といえます。この位置は､ 月の大きさ２個分(１度)の大きさだけ本影の中心から月の中心がずれています。さらに外側の４番の月では半影錐に接していますので､ 半影月食を起こす限界になります。月の中心が本影錐の中心から月の大きさの３個分(１.５度)離れています。
このように考えてみると、皆既月食が起こる可能性が一番低く幅は約０.５度、地球上のどこかで皆既日食か金環日食が起こっている可能性と､ 部分月食以上の月食が起こっている可能性がほぼ同じで１度、地球上のどこかで部分日食以上が見られる可能性と､ 半影月食が起こる可能性はほぼ同じで１.５度となります。結局、日食と月食が起こる可能性はほぼ同じといえます。
１００年間に起こる日食・月食の回数は、金環日食・皆既日食が合計１５３.７回、月食は皆既月食７１.６回、部分月食８２.７回で、 合計１５４.３回だそうです(出典：天体観測ハンドブック)。だいたい同じような数値になっていますね。
次に、昇交点や昇交点が太陽を向く前後何日以内に月が通過すれば日食・月食になるか考えてみます。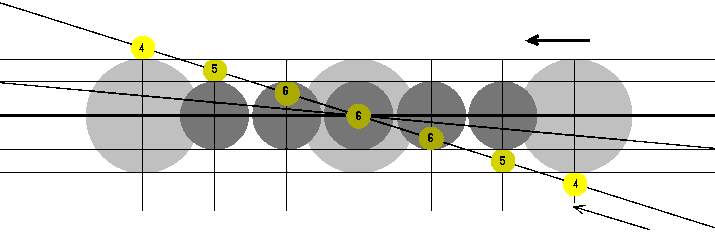
右側の４の位置からスタートしたとします。半影月食が起こっています。その後、月が１公転して再び４に戻ってきたとき､ 地球の影はどこにあるでしょうか。白道の傾きは約５度ですから、図で１だけ上がると１１だけ左にずれます｡ ４から５までたてに０.５度ですから横に５.５度になります。縦線１本分左にずれるのに５.５日かかることになります｡ ４から左側の５まで進むのに２７.５日、左側の４まで進むのに３３日(月がこの区間を動くのにも１日かかる)かかります｡ ２７日では月は１周してくることはありませんから、半影月食どうし以外で満月が２回連続して月食になることはありません。
半影月食と部分日食が起こる可能性が同じですので、部分日食が連続した新月に起こることもあります｡ 皆既日食や金環日食が起こった前後の新月は日食となることはありません。
皆既月食と皆既日食(金環日食)の組み合わせはどうでしょうか。右側６の位置で皆既月食が起こったとし､ 左側５の位置(の真後ろ) で皆既日食が起こることは考えられます。この間１６日半で半月より１日だけ(月が右６から左５へ追いつく半日を引いています) 長いので、皆既日食皆既月食が連続して起こる可能性もわずかにあります。
当然のことですが、日食は影の中に入らないと見えない現象です。地球上で太陽の見える位置にいても、日食が見えないことがあります｡ これに対して、月食は起こっていて月が昇っていれば(昼間でなければ)必ず見えることになります｡ 従って見える機会としては月食の方が多いことになります。
６．日食・月食は予報できるか
現在では、太陽や月の運行のようすがはっきりわかっており、いつ日食や月食が起こり、どこでどのように見えるかも計算で求められています｡ それでは、昔の人はどうだったのでしょうか。太陽と月の位置を正確に観測しそこから月と太陽が重なるかどうかを求めることはできたようです｡ 何年も先のものまでというのは無理だったかも知れません。
(1)サロス周期の発見 日食・月食の起こり方には不思議な規則性があることが大昔から知られています。それについて考えてみることにします｡ 規則性を見るために１９７２年から２０２０年までの各年の何月何日に日食・月食があるかをまとめてみました｡ ８６年をのぞく７２年から２０１０年までは各年の天文年鑑から、２０００年から２０２０年までは国立天文台の暦計算室のサイト (http://eco.mtk.nao.ac.jp/koyomi/)から､ ８６年は天文シュミレーションソフトで求めています。
(2)サロス周期の不思議 サロス周期がどうしてできるか考える事にします。まずサロス周期を求めます。１８年は６５７４.３５９６日(365.2422*18)あります｡ 日食は新月の時にしか起こりません。したがってサロス周期は新月になる周期の倍数になります。新月から次の新月までの長さは１朔望月といい､ ２９.５３０５８８９日あります｡ 先ほどの日数をこの数値で割って２２２.６。これより少し大きな整数の２２３が､ サロス周期の間に朔望月が繰り返される回数になります。従ってサロス周期は６５８５.３２１３２日になります｡ １８年の内に閏年は３〜５回あります※１ので、サロス周期は１８年と１０〜１２日と７時間４３分(約８時間)になります。
サロス周期には不思議な一致がいっぱい見られます。例えば月が昇交点を通過してから次に昇交点を通過するまでの日数を考えてみます｡ この日数を１交点月といいます。昇交点に月が来ないと日月食が起こりませんので交点月は非常に大事です｡ １交点月は２７.２１２２日あります｡ ２４２倍すると６５８５.３６日になります。また、月は地球に近づいたり遠ざかったりしています｡ この周期は１近点月といい､ ２７.５５４６日です。２３９倍すると６５８５.５４日です。地球に近づく遠ざかるは､ 金環日食になるか皆既日食になるかの要素として大事です｡ 最後に食年の長さです。これも１９倍すると６５８５.７８日になります｡ 日月食が起こるかどうかが決まる周期の倍数どれもが６５８５日になるという奇妙な一致が見られます※２。整理してかきます。
(データは天文年鑑２００８年版使用)
1 朔望月 = 29.5305889日 223 朔望月 = 6585.32132日 新月(満月)になる周期
1 交点月 = 27.2122209日 242 交点月 = 6585.35745日 昇交点を通過する周期
1 近点月 = 27.5545498日 239 近点月 = 6585.53740日 近地点を通過する周期
1 食 年 = 346.620079 日 19 食 年 = 6585.78151日 昇交点が太陽を向く周期
何回繰り返すかという数値に注目すると、２４２以外は素数で、そうでない２４２(11*11*2)もその他の数値とは共通の約数を持ちません｡ サロス周期の中では、日月食の度にそれぞれの周回数を求めたときに少数以下の値が異なります。そのため、サロス周期内では､ 毎回欠ける大きさや方向､ 見られる地域が変わります。
※１ １８年間の閏年の回数
２０００〜２０１７年だと2000,2004,2008,2012,2016年の５回
２０９７〜２１１４年だと2104,2108,2112年の３回
※２ 実際には、朔望月の倍数(サロス周期)と交点月の倍数とが完全に一致しているなら､ 食年の倍数も完全にそれに一致するはずです。例えば昇交点上に月がいて、その延長上に太陽が来た時(日食が起こっている)を考えます｡ サロス周期後には、何朔望月かが過ぎていますから、新月になっています。このことから月の延長上に太陽がいることがわかります。また､ 何交点月かが過ぎていると仮定しましたので、月は昇交点に戻ってきています。これを３段論法で考えると､ 昇交点に月がいる＋月の向こうに太陽がいる→昇交点に太陽がいる という図式になります。昇交点に太陽がくる周期が食年で､ 何回あったかはわかりませんので何食年かが経過していることになります。食年の倍数が一致するのは当然といえます。
(3)日食家族 サロス周期を経た後に起こる日食はよく似た形で起こります。これらをまとめて１つの系列とする考え方ができます｡ 例えば、先ほどの日月食の発生日を書いた表では、１９７２年１月中旬の金環日食と１９９０年１月下旬の金環日食､ ２００８年２月上旬の金環日食は同じ系列に属すると考えます。これらの日食は非常によく似た形で起こっています｡ １９７２年から１９８９年までの間には、日食は３９系列あります。１サロス周期の中でも系列の数は増減します｡ 例えば２０１１年７月１日に起こった部分日食の１サロス前にあたる１９９３年６月中旬には日食が起こっていません｡ 新しい系列が加わったことになります。この場合、６月２日の日食と親子関係として同家族にします。各食年の､ 昇交点で起こる日食(昇交点日食)、降交点で起こる日食(降交点日食)を一つ一つを日食家族として扱い、新たにできた日食の系列は､ 家族内の子どもとして扱います。１サロス周期は１９食年ですので、日食家族は３８家族になります。新たに子どもができ続けていくと､ 日食がいっぱい起こるように見えてきます。実際には、子どもができた家族はしばらくすると親が日食を起こさなくなります｡ その理由は次で説明します。
昇交点日食か、降交点日食かは表からは区別できません。その日食とその前後に起こる皆既月食との組み合わせで考えます。例えば､ ２００７年には３月４日と８月２８日の２回皆既月食があります。それぞれの直後の３月１９日、９月１１日に部分日食が起こっています｡ ３月のは北半球で、９月のは南半球で見られましたので、３月は昇交点日食、９月は降交点日食になります｡ 同じ帯上にある日食は同じ種類になります。従って、２００９年７月２２日トカラ列島で見られた皆既日食は､ ２００７年９月の日食と同じ帯上にありますから降交点日食となります。
月食にも同じように考えると家族があるはずですが、月食家族という用語はあまり使われていないようです｡ 日食に比べて影の中心帯がわかりにくく、月食の違いがわかりにくいからでしょう。もちろん、昇交点月食・降交点月食はあります｡ 昇交点日食と帯が重なっているのが降交点月食です。
(4)サロス周期内で日食の起こり方がどう違うか サロス周期が、一致するといっても、微妙にずれがあります｡ この影響を考えてみます。その前に、サロス周期そのものに、少数以下の端数があります。これからどういう事が起こるのでしょうか｡ 単位は日ですので、１日の長さとは同期していないことを示しています。つまり、少数以下の約３分の１日の端数があることによって､ たとえばある日の正午に日食が起こったとすると、１サロス周期経過後の日食は午後８時に起こることになります。夜ですので､ この日食を見ることはできません。実際に見ることができるのはこの時間帯が昼間のところ、地球上の経度で１２０度西側の地域になります｡ 日食が起こる時間は遅れ、見られる地域が西にずれてくるのです。ところがこれも偶然なのですが、３サロス周期後になりますと､ 地球を１周してほぼ元の位置に戻ってきます。５４年後には、再び日月食が見られることになります｡ 正確にはサロス周期の小数部の３倍は１に０.０３６、時間にすると５２分だけ不足しています｡ その分、経度で１３度東にずれることになりますが、ほとんど同じ地域見られると言っていいでしょう※｡ ３サロス周期後は、１年の長さより１ヶ月ほど長く、起こる月が遅れていくことなりますが､ 日食の周期に何らかの影響を与えるものではありません。
※１３度東にずれるのは、太陽(月)から見て、地球の真ん中に見える地点(地上で太陽が頭上にある地点)の経度です｡ 一つの子午線(例えば東経１３５度)が、地球の真ん中に見えるようにしながら地球儀を回してみると、地球(上の各地点) が上がったり下がったり回転したりするように見えます。その影響で、以前より東側に影が落ちても、西側の地点が影に入る (日食になる)こともあります。
(5)日食家族の世代交代 １サロス周期と２４２交点月の間にも３０分の１日ほどの差があります。足りません｡ 昇交点で起こった月食があったとします。次の回では、月がまだ昇交点に達していないことになります｡ 昇交点の手前側は黄道より南ですので、月が地球の影の中を横切る位置がわずかに南へずれます。サロス周期が来るごとにずれ､ そのずれが大きくなればそのうちに影を横切らなくなります。時代をさかのぼれば、北の端を横切る半影月食に始まって､ 部分月食、皆既月食へと変化してきました。日食も同じように、北極をかすめるものから始まり、次第にその中心線が南下していき､ 南極をかすめるようになって日食が見られなくなります。降交点で起こる日月食の場合、動きの向きはこの逆で、南から北へ移り変わっていきます。
日食家族の１系列が起こす日食について考えてみます。１サロス周期と交点月の不足分は、角度で０.４８度(３６０×不足分÷交点月の日数)あります｡ 皆既日食を起こす範囲は約２２度(月が地球の影を横切る図を参照)ですから、４５回ほど繰り返すことになります。年数で８５０年になります｡ またその前後それぞれ１１回(２００年)ほど部分日食を起こします。
日食家族には１２００年ほどの寿命ができることになります。尽きればどうなるのでしょうか｡ 昇交点日食の寿命が尽きる直前を考えてみます。この頃には月がずいぶんと南によっています。月が地球を横切る図では､ 右側の４に近い位置に相当します。ここで日食を起こしたときは、次の新月の時には左側の４に相当する位置に達していません｡ ３と４の間に相当する位置にいますので、部分日食を起こしています。新しい日食系列が生まれたことになります｡ この一つの例が先に述べた２０１１年７月の日食です(降交点日食ですが)。降交点日食では図の上下(南北) が入れ替わるだけで、全く同じ現象が起こります。
子どもができて、しばらくすると親がなくなるということを繰り返して日食家族が受け継がれていきます｡ この現象を日食家族の世代交代といいます。これに従えば、親も子も同じ家族なので、同じ日食家族に含めて考えることになります｡ 世代交代は交点月(食年)の不足分を解消する方法ですので、それから考えても、親と子は同じ家族に入れて考えるのが正しいでしょう。
参考になるサイト 日食とサロス周期 http://www.hucc.hokudai.ac.jp/~x10553/guide/guide.html
解明できていないこと
３サロス後の日食の見られる位置がどのように見られるか(数式ばかりになるので解明できても簡単には解説できないと考えられる)
日食家族の寿命が一定でないこと
７．天体の食・掩蔽現象
一般に○○食と言われるものは、ほとんどが掩蔽現象です。食は影に入って見えなくなる現象ですので､ 自らが光っていない惑星や衛星のような天体だけに起こります。あまり厳密に考えずに、掩蔽も含め食としてどの様な現象があるか､ それから何がわかったのかをまとめることにします。
食・掩蔽現象を観測できるのは、ほとんどの場合、星を観測していて急に暗くなった、突然明るさが戻ったというような現象として観察されます｡ いつ、どれくらい明るさが変わったかということを正確に記録できるようにすることが大切です。影が見えているわけでもないし､ 場合によっては星そのものも光がその方向からやってきているというだけで、形や大きさがわからないこともあります。
(1)人工衛星の食
人工衛星は、日没後や日の出前に何個か見られることがあります。ふつうは、地平線から上って、地平線に沈んでいくのですが､ 中には、空に突然現れたり、急に消えたりするものもあります。これは、地球が作る影に入ったり、影から出たりするからです。
静止衛星などで問題になるのは、春分や秋分の頃の真夜中に地球の影に入ることがあります。太陽電池で発電できなくなりますから､ 運用が休止されることがありました。最近では、電池などを使うことによってそのようなことがなくなっています。気象衛星ひまわりで､ 画像の配信がなくなるのは、影にはいるというより、太陽が写り込む事が問題なので、これを避けるために休止することがあります｡ http://mscweb.kishou.go.jp/panfu/operation/reference/equinox/index.htm
(2)木星やガリレオ衛星による食・掩蔽
惑星の周りを回る衛星でも、惑星との間で食や掩蔽を起こします。木星の４大衛星(ガリレオ衛星)は双眼鏡でも観察できるので､ 木星の影に入ったりする(木星に食される)のが観察できます。実際には木星本体とずれた位置で、突然消えたり、出現したりします｡ この現象はしばらく観察し続けていないと確認できない現象です。例えば、下の図は､ １９９０年１月の２３日２５日２７日の３日間１時間おきに撮影した木星とガリレオ衛星の写真です (反転していますので、黒いところが衛星や木星になります)。中央の大きな黒円が木星本体で､ 衛星には内側のものから順に番号をふっています。ここで１をつけた第１衛生イオの公転周期は１.７７日ですので､ ２３日２３時１５分と２５日１８時ちょうどには、木星に対してほぼ同じ位置にいます。そう考えて図をよく見ると､ ２５日２０時ではイオがいるはずのところに写っていないことがわかります。木星に食されているのが原因です。それ以前の､ １８時１９時は木星の向こう側にいますので、掩蔽されていて写っていません。
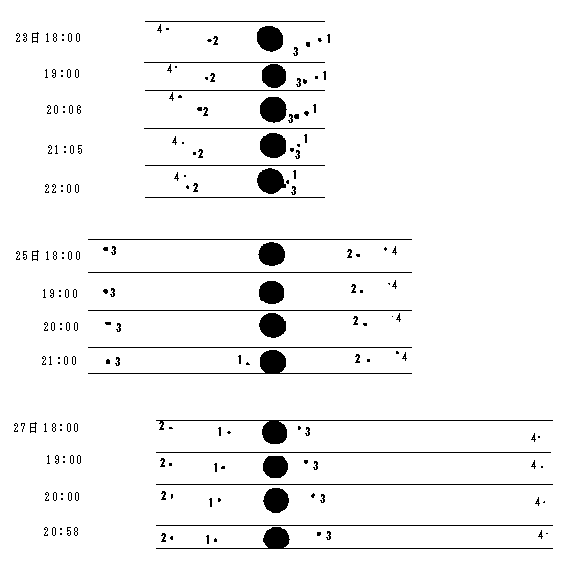
木星の衛星が木星の向こう側を通ればこのようになります。今度は手前側を通るときを考えてみます。木星の手前側を通り抜けるわけですから､ 木星の面に重なって衛星が見えます。衛星が木星を隠しているのですが、木星の方が大きすぎて隠しきれません。このような場合､ 掩蔽といわずに衛星の木星面｢通過｣といいます。また、衛星の影が木星面の上に落ちて黒い点になって見える場合もあります｡ これを見るのには、少し大きめの望遠鏡が必要です。
ガリレオ衛星の公転面の昇交点の方向(昇交点黄径)と、太陽から見た木星の方向(日心黄径)が同じになると(正反対になるときも)､ 地球に日月食が起こるのと同じ理由で、ガリレオ衛星どうしで隠したり隠されたり(掩蔽)、影に入れたり(食)といった相互現象が起こります｡ 衛星の大きさや明るさ、運動の方向が複雑に変化しますので、起こったときの起こり方やその程度、継続時間は微妙に変化します。この現象は､ ２００９年１月から２０１０年４月に、その次は２０１４年８月から２０１５年８月にありました｡ 木星の公転周期の半分である約６年ごとに起こります。
(2')土星の衛星の食(食・掩蔽)
木星の衛星の公転面と木星の公転面とはわずかに傾いているだけなので、木星とガリレオ衛星間の食掩蔽は１年を通してみることができます｡ これに対して、土星の衛星の公転面と土星の公転面は３０度近く傾いているので、地球と月との間で日月食が起こるときと同じ様な関係になって､ 初めて起こります。この時、地球から見ると土星の輪は真横から見ることになり、非常に細くなり、場合によっては全く見えなくなることがあります｡ 例えば２００９年９月４日に輪がみえなくなりました｡ この前後１年間に土星と衛星の間での食・掩蔽が起こっています。衛星相互の間での食・掩蔽も起こっていますが､ 土星の衛星ではテイタン以外は暗く観測には中〜大型の望遠鏡が必要でした。
土星の輪に土星の影が写っていたり、土星本体に輪の影が写っていたりすることがありますが、明るさの変化として観測することはないので､ これを食現象とした記録はありません。
(3)星食(掩蔽)
月が太陽を隠して日食を起こすように、月が星を隠して見えなくする事(掩蔽)があります。この現象を星食といいます｡ 隠す星が恒星の場合恒星食といい、惑星の場合は惑星食といいます。
星が隠されても、昼間では見えません(望遠鏡を使えば１等星は見えるかも)ので、観測できません。また、月が沈んでいてもだめです｡ 新月の前後は星食が観測しにくいといえます。逆に満月の前後は、月明かりが強くて星が見づらくなります。観測できる星食は限られてきます｡ 上弦月の頃は、暗い縁から星が隠れ、明るい縁から現れます。下弦の月ではこの逆となります。
月の通る白道はほぼ黄道に沿っていますので、ほぼ黄道沿いの恒星が隠されることになります※１。例えば１等星では､ さそり座アンタレス､ しし座レグルス、おとめ座スピカがその対象となります。おうし座アルデバランも隠されることがありますが､ 地球上の地域によっては､ その現象が全く起こらない場所もあります｡ 変わったところでは、すばるやプレセペといった星団も隠されることがあります。
１年単位で見ると白道はほぼ決まった位置にあります。隠される星はほぼこの線上にあるときだけです。１年のうちでは､ 毎月同じ星の近くを月が通ることになり、黄道近くの星でも隠されないものが出てきます。しかし､ 白道に注目してみると先に述べた昇交点の移動によって少しずつずれていきます。何年かすると違う星の近くを通ることになります｡ そして昇交点が１回転すると、また元の星の近くを通るようになります。昇交点は１８.６年で１周します※２ので、その間に､ 食が続く時期は１回または２回あります。例えば、すばる食は２００５年から２０１０年にかけて起こっていましたが､ その後しばらくは起こらなくなり、次に起こるようになるのは２０２３年です。
星食を観測することによって、月の運動のようすを調べたり、地球の自転のようすなどが詳しくわかります｡ 最近では、レーザーで月までの距離を測ったりといった方法でより正確にわかりますから、星食から求めるということはなくなってきました｡ どちらかというと星の位置精度の向上に使われているようです。
星が月の南または北の縁ぎりぎりを通る現象を接食といいます。月の山や谷の形によって星が現れたり消えたりします｡ これによって、月の表面のでこぼこのようすが詳しくわかります。これも｢かぐや｣などの探査機による測定データから知ることができ､ 二つのデータを比較検討してるところです。
(3')惑星食 惑星食は、相手の天体によって呼び方が変わります。恒星食に比べると起こる回数は少ないようです｡ 惑星は恒星より明るいことが多いので見応えがあります。
※１ 白道は黄道に対して５.１５度傾いていますから、月は黄道の南北両側この角度の範囲を通ります｡ また月は最大で半径０.２８度の大きさに見えますので、この範囲の星を隠すことができます。地球上で月の南中時高度が０度の地点では､ ９０度の地点に比べて月の位置が最大で１.０４度ずれて見えます(視差)。これらの要素を最大限に見積もると､ 黄道の南北６.４７度の範囲が地球上から見て星食が起こる可能性のある範囲となります。
※２ 昇交点が１周する周期は、１食年の逆数と地球の公転周期の逆数との差を計算し、その逆数を撮ることで求められます｡ この計算式は、惑星の会合周期を求めたり地球の自転周期を求めたりするのと原理は同じです。
(4)惑星による恒星食(掩蔽)
惑星も恒星を隠すことがあります。この現象を観測しているといろいろなことがわかることがあります。
１９７７年３月１０日に天王星が恒星を隠しました。見ることができたのは南インド洋と南極大陸だけだったのですが､ この時恒星が隠れる３０分ほど前に５回わずかに星が暗くなりました。そして、再び天王星から出現した後､ 先ほどと逆の順番でわずかに星が暗くなりました。この現象は、天王星に５つの輪があり､ それによって恒星の光が弱められたために起こったと考えられました。天王星の輪については発見者であるハーシェルが､ 輪が見えるといっていたのですが、当時の望遠鏡では観測不可能であるし、以後の観測でも見つからなかったので誤りとされていました。
小惑星も恒星を隠すことがあります。小惑星による恒星食では、恒星より小惑星の方が暗いことが多く､ 恒星が暗くなるようすから小惑星に隠されたと判断できます。恒星が隠れ暗くなっている時間から小惑星の大きさがわかります｡ 望遠鏡では小惑星の大きさは測定できないのですが、この方法で大きさを、何地点での観測をあわせることで形､ あるいは衛星があるといったことまでわかります。薩摩川内宇宙館を中心に精力的に観測されています｡ http://sendaiuchukan.jp/data/occultshort.htmlに詳しく書かれています。
(5)日面通過(惑星による太陽の掩蔽)
地球より内側をまわっている水星・金星は太陽の前を横切ることがあります。水星・金星は太陽に比べて非常に小さく､ 太陽の表面上を真っ黒な点となって移動していきます。この現象を日面通過といいます。水星や金星の公転軌道は､ 地球の公転軌道に対して傾いていますので、内合や外合の度に起こりません。昇交点や降交点上に惑星・地球がいるときのみ起こります。
(5a)水星の日面通過 太陽の前面を水星が横切る現象です。
水星軌道の降交点や昇交点の延長上に地球が来るのは、５月８日と１１月１０日頃です｡ 水星の日面通過が起こるのは毎回この前後数日の間に内合になるときです。
水星の会合周期は１１５.８８日です。４１会合周期が１３年＋約３日、１４５会合周期では４６年−１日です｡ 従って一度日面通過が起こると、その１３年、３３年、４６年後に日面通過が起こる可能性が高くなります。
水星の軌道はだ円形ですから、水星は太陽から遠ざかったり近づいたりします。５月頃は遠日点付近にいます。内合の頃の水星は､ 地球に近づきます。距離が近いと見かけの速さは早くなりますので、日面通過となる区間を早く通過します。そのため水星の日面通過は､ １１月より５月の方が少なくなります。１９７０年から２１１１年に日面通過が起こる(起こった)日は次の通りです。 ()内の数値は間の年数です。規則性が読み取れたでしょうか。
参考文献 天体観測ハンドブック 天文年鑑２００４年版 誠文堂新光社
(6)食変光星
連星の中で、太陽(地球)からみて恒星の回転面が真横になっているとき、連星の恒星どうしが互いに隠したり隠し合ったりします｡ このとき、星は暗く見えますので、周期的に明るさが変化します。これが原因で、明るさが変化する星を食変光星といいます｡ 恒星が非常に遠くにあって、二つあるのが望遠鏡で見えない場合でも、恒星が２つあることがわかります。また､ ドップラー効果を利用した運動速度の測定もあわせて計算することで、両星の質量や直径を求めることができます｡ 食変光星は、二つの星の大きさ、性質などによって明るさの変化の様子が違います。変光のようすから、恒星の性質もわかります。
最近ではトランジット法といって、恒星の周りを回る惑星が恒星を隠す事によって起こる光度の変化が測定できるようになってきました｡ これを利用して、系外惑星が発見されています。実際には太陽に木星サイズの惑星があるとして考えてみます｡ 木星の大きさは太陽の１０分の１ですから面積は１００分の１になります。遠くの星から見て、太陽の前を木星が横切ったとしても､ 明るさは１％暗くなるだけです。明るさの測定はかなり正確に計る必要があります。
８．日食・月食の用語
(1) 日食の見られる地域：日食地図(日食図)
地図上に日食が見られる範囲を記入した図を日食地図といいます。日食図と書かれている場合もあります。図からは､ 地図上に表された地域では日食がどのように見られるかがおおよそのようすがわかります。図とともに考えてみます｡ 図は、国立天文台暦編纂室のサイト(http://eco.mtk.nao.ac.jp/cgi-bin/koyomi/eclipsex_s.cgi)で閲覧できます｡ このサイトの図を使って解説することにします。解説の都合上、経緯線・日本以外の海岸線を消去した(図の容量を小さくするためです)後､ 着色したものを使用します。実際には、解説で説明する線だけでできています。
ふつうの日食地図：何がふつうで、何がふつうでないかは決められないのですが､
地球上に月の影が完全に落ちている場合の日食地図を考えます。２００９年７月２２日トカラ列島で見られた皆既日食の時のものです｡
全体として鼓のような形になっています。地図の形式によっては多少違った形になります。真ん中を横切って赤く塗られた所が､
皆既日食の見られたところです。暦編纂室の図では北限界線、南限界線、中心食線(影の中心が通るところ)､
各時の影の輪郭が記されていますが、図では一色にしています。金環日食を表す図ではこの範囲が金環日食の見られる範囲となります｡
皆既日食では中程が太く、逆に金環日食では細くなります。
そのほか青く塗ったところが部分日食の始まりと終わりが見られた所、水色が部分日食が見られたものの始めまたは終わりが見られなかった所です｡ 月の影の中心は、３時間半ほどかけて地球を西から東に横切っていきます。そのため、西(左)側の水色部がはじめが見られないところ､ 東(右)側が終わりが見られないところになります。何時にどのように見られるかは、別の表や図から判断する必要があります｡ 着色していないところでは、日食は全く見られません。
ここで、日食地図に書かれている境界線の意味と名称を整理しておきます。
青色区域の北側や南側の、塗っていないところとの境界線(桜色)は日食が見られる所と見られない所との境界線になりますので､ 日食北(南)限界線といいます。
その他の境界線は以下に列挙します
西側の水色区域の境界線は西側から順番に
黄土色：日の出と同時に欠け終わる所＝日出復円線(ふくえんせん)
黄橙色：日の出に最も欠けている所 ＝日出食甚線(しょくじんせん)
黄 色：日の出と同時に欠け始める所＝日出初虧線(しょきせん)
同様に東側の水色区域の境界線は順番に
紫 色：日没と同時に欠け終わる所＝日没復円線
マゼンタ：日没に最も欠けている所＝日没食甚線
藤 色：日没と同時に欠け始める所＝日没初虧線
初虧線と復円線はつながっています。その場所では欠け始めると同時に終了しますから、日食は一瞬の間だけ見られます｡ 月の半影の端がかすめて通る場所になりますから、日食北(または南)限界線と接しています。また､ 欠け始めと欠け終わりの真ん中に最もかける時刻がありますので、食甚線とも重なります。４本の線がこの１点からのびていきます。
北に偏った日食地図：地球が月の半影を部分的に横切るとどうなるのでしょうか。図は２０１２年５月２１日の金環日食のものです｡
日食北限界線がなくなり、東西にある日食が部分的に見られる地域がつながっています。日出復円線と日没初虧線、日出初虧線と日没復円線､
日出食甚線と日没食甚線とが北側でつながっています。それでは、それぞれの接点はどこになるのでしょうか。
日出復円線と日没初虧線で考えてみます。接続点では、日の出と日の入りが同時に起こっています｡このようなことが起こるのは､ 北極圏内で夏なら北の地平線上を太陽がかすめて通る時、冬なら南の地平線上に一瞬だけ太陽が顔を出すときになります｡ 始まりと終わりが同時ですから、日食は太陽が地平線をかすめる一瞬だけ起こります。
この時を宇宙から見たとすると､ この位置は月の影が地球を通る最も北側の端になります。日食北限界線上にあるともいっていいでしょう｡ 日出復円線と日没初虧線の最も北側､ 言い換えれば高緯度側になる場所でつながっています｡ 北極に最も近づく所が線の変わり目といえます。日出初虧線と日没復円線､ 日出食甚線と日没食甚線についても､ 北極に最も近づく所が線のつなぎ目となります。
月の影の一部だけが地球の南半球を通過した場合、南北が逆になるだけで同じような日食地図ができます。
もっと北に偏った日食地図：２０１９年１月６日、日本で部分日食が見られるときのものです｡
本影が地球から離れたところを通過するため、皆既日食や金環日食の見られる地域がありません｡
冬に見られる日食なので北極(×印で示しています)から離れたところに日食の見られる地域があります｡
日出初虧線と日没復円線といった線どうしがつながっているのは先ほどの場合と同じです。
この時期の日食地図では不思議なことが起こります。食甚線が初虧線や復円線から外側にはみ出しています｡ この場所では日食はどのように見えるのでしょうか。
食甚線上で考えてみます。日出食甚線と日没食甚線のつなぎ目で考えてみます。ここでは３つの現象が同時に起こっています｡ つまり、日の出とともに日食が最大になり、太陽は直後に沈んでいきます。この場所では、日食の始まりも終わりも見られないのに､ 日食を見ることができます。
このような、欠けた太陽が昇ってきて、欠けたまま沈んでいく場所は、図の線からはみ出した場所にあります｡ その場所は次の３本の線に挟まれた地域にあります。１つめは北極を中心として、日出復円線と日没初虧線との接続点､ 日出初虧線と日没復円線との接続点を端点とする円弧、２本目は日出初虧線、３本目は日没復円線です｡ この地域では最初から最後までというようにいかないけれど、日食が見られるということで図には水色 (本来の水色区域も水色です)に着色しています。
夏の日食では、これと逆のことが起こる地域があります。日食が始まってから太陽が沈み､ 終わりかけると太陽が昇ってくるという不幸？な地域です。２０１２年の日食地図では図に示せるほど広くはないので､ 記入していません。青く塗った地域の中にわずかですがあります。
日本で使う限り、日食地図は単純でわかりやすいものです。北極圏や南極圏、その近くの地域では読み取りに注意が必要な場合があります。
星食の見られる区域を示した地図も、日食地図に似たものになります。星食では、日食の見られる区域の幅が、月の太さで描かれます｡ 惑星による恒星食では、惑星の太さでになります。木星や土星などの場合はその方向さえ向いていれば見ることができます｡ 小惑星では、その直径と同じ幅で掩蔽帯ができます。
月食や日面通過は、月や太陽が出ていれば見られるので、開始時刻・終了時刻にその天体が出ている半球を示す図で描かれます。 この図も日食地図が変形したものと見なせます。
参考文献：天体観測ハンドブック 誠文堂新光社
(2)日食や月食の状態を表す用語
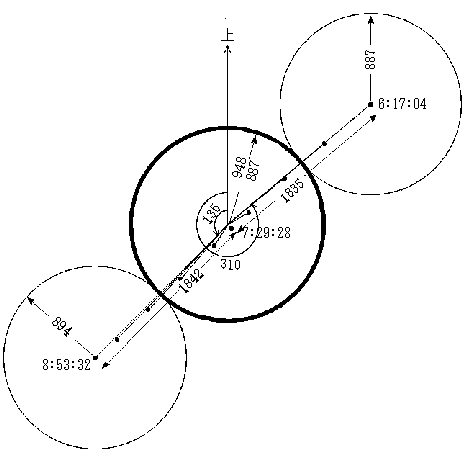
日食や月食時には、状態を表す数値が公表されており、そこからどのようになっているかを判断することができます｡ 例えば、２０１２年の金環日食の時の明石での予報は以下の通りになっています(国立天文台暦編纂室のサイトより抜粋しました)。
それぞれの用語の意味は以下の通りです。なお、隠される天体をＡ、隠す天体をＢと表すことにします｡ 日食の場合Ａが太陽でＢが月に､ 月食の場合Ａが月でＢが本影または半影になります。
実際にデータを使って作図してみます(右図)。
まず、どれくらいの長さをどれくらいの大きさで表すかを決めます。その大きさに従って、図の中央に太陽を書きます｡ 太陽の中心から図面上方向に線を引き、これを実際に見たときの上(天頂)方向とします。
６時１７分４秒(部分食開始時刻)の月の位置を書いてみます。太陽の中心の位置で､ 上方向から反時計回りに３１０度の方向に線を引き、１８３５に相当する長さのところに印を入れます｡ ここが部分食開始時刻での月の位置の中心になります。ここを中心に月の大きさにあわせて円を描きます｡ この時、部分食が始まる時刻ですから、月と太陽が接しているはずです。
同様に、７時２９分２８秒(食甚)と８時５３分３２秒(部分食終了)の月の位置､ ２０分ごとの月の中心位置も作図しておきます。食甚時の月の輪郭は太陽を表す太線の内側の境界です｡ 黒く太くなっている部分が、月が太陽に最も入り込んだときの太陽の状態を表しています。
日食が起こる場合を考えてみます(下図、太陽・月・地球の大きさはでたらめです)。月が地球と太陽の間に割り込むわけですから､ 太陽−月−地球はこの順番で一直線に並んでいます。また、地球から見て月は太陽の光が当たっていない面が見えるわけですから､ 月は新月になっています。日食は新月の時に起こる現象です。
)。本影錐の中では、太陽が完全に月に隠される事を確認してみます。地球上
(水色)で本影錐の中の点、例えばＡ点で考えてみます。Ａ点から月の両端を結ぶ線が月の大きさになります｡
太陽との大きさを比べるために太陽の位置まで引っ張っていきます。この時にできた暗黄色のＡ'
の円と位置が太陽と比較した月の位置と大きさになります。明らかに太陽の赤丸を覆っているのがわかります。この状態が皆既日食です。<部分日食> 次に、太陽の下端と月の上端というように反対側どうしを結ぶ線を考えてみます｡ 太陽と月の間の一点を頂点とする円錐型の図形がかけます(図中月地球間では明るい灰色の部分)。この円錐形を｢半影錐｣といいます｡ どうしてそういう名前になっているか考えてみます。半影錐内の地表の一点Ｂ点に注目します。先ほどと同じようにして書いてみると､ 太陽と月の大きさ・位置の関係は図中Ｂ'の円となります。この円は太陽の一部分だけ隠しています。この状態が｢部分日食｣です｡ 太陽の一部分がが隠れ、半分だけ影になっている状態なので｢半影｣錐と呼ばれます。半影錐の縁ではここと月太陽を結ぶ線が直線上に並びます｡ これは太陽と月が横にくっついて見える事を示しています。これより外側では太陽と月は離れて見えます｡ 半影錐の内側が部分日食の見える場所といえます。
<金環日食、金環・皆既日食> 上の図では、本影錐が頂点までできないうちに地球が割り込んできました｡ 頂点まで書けばどうなるのでしょうか。書いてみました(下図)。
ところで３番目の図のような場合どうなるのでしょうか。Ａ点は本影錐の頂点より手前側にありますので皆既日食を見ることができます｡ Ｃ点は今は本影錐の中にありませんが、地球が月が作る影の中を横切っていきますので、本影錐の中に入っていきます｡ その位置は頂点より先になりますので、金環日食が見られる事になります。Ｃ点の時刻は､ 自転によって薄水色の部分に入る直前なので夕方になります。明け方にも金環日食が見えていた場所があります。Ａ点は正午頃となります｡ 同じ日食でも場所(時刻)によって皆既日食・金環日食と違う場合があります。このような日食を｢金環皆既日食(ハイブリッド日食)｣ といいます。金環日食から皆既日食に変わる場所では、月の縁にある高い部分がさえぎられ、とぎれとぎれの環が見られます。
金環日食や皆既日食が起こったりするのは、まず第一に月や太陽の見かけの大きさが変化しているためです。これは､ 月や太陽までの距離が変化するためです。ふつう惑星や衛星がその主星(この場合太陽や惑星)の周りを回る軌道の形は決まっていて､ その形はだ円形になります(ケプラーの第一法則)。円ではないので距離が変わる事になります｡ 実際地球から見た太陽や月の大きさは変化している様子もわかっています｡ 二番目は、地球から月までの距離(月の公転半径)が、月が作る本影錐の高さとほとんど同じであることです。短すぎても､ また長すぎてもどちらか一方にしか起こらないことになります。月までの距離はだんだん大きくなっていることが知られています (クリックすると説明文のあるところに進みます)｡ 何千万年か前は皆既日食だけが、何千万年かすると金環日食しか起こらない事になります。
２．月食の起こり方
月食の起こり方を考えるために最初の図に戻って考えてみます。図を再度載せます
上の図で、月と地球の位置を変えて考えてみることにします。今度は黄色が地球、水色が月になります。図に書かれた月は大きくなりすぎています｡ 実際にはＡ点・Ｂ点を示す黒丸の大きさくらいでしょうか。これで考えてみましょう。本影錐の中にあるＡ点の月は光が当たっていないので真っ暗です｡ これが｢皆既月食｣です。
半影錐の中にあるＢ点の月は太陽の光が当たっているので明るいのですが､ 一部地球に隠されていますのでわずかに暗くなっています。この状態が｢半影月食｣です。暗くなる割合は、本影に近づくにつれ大きくなり､ 半影錐の縁に近づくにつれ明るくなります。暗くなっていると言っても、目で見てわかるというものではありません｡ 薄雲がかかっている方が暗く見えることもあります。本影に半分かかっているときが｢部分月食｣です。皆既月食の時もそうなのですが､ 本影に入っているといっても、地球の大気中を通り抜けた赤い光が屈折して月面を照らしているので、完全の真っ黒になるのではなく､ 赤暗く光って見えます。光が通り抜ける様子を知るためには、月食中に月面近くから見た映像も参考になります。月探査機｢かぐや｣ のサイトにあります(http://www.jaxa.jp/press/2009/02/img/20090218_kaguya_2.jpg)。地球の周りから光が漏れてきているようすがわかります。
最後に月食がどのようなときに起こるか考えてみましょう。図の黒い点ではわかりにくいので、再び大きさを水色の円にまで拡大してみます｡ 黄色で書いた地球から水色で書いた月を見ると明るい面ばかりが見えています。この状態は満月です。月食は満月の時に起こる現象です。
３．新月・満月の度に日食・月食が起こらないわけ
新月や満月の時は太陽−地球−月が一直線に並んでいます。単純に考えると、満月の時には、月は地球の影に入って月食を起こし､ 新月の時には太陽を隠して日食を起こしそうです。実際には、満月といっても月食にはならないし、新月には日食が起こってはいません｡ どうしてでしょうか。簡単に答を言えば、満月の月は地球の影の上か下を横に通り抜けるし、新月の月は太陽の上か下を通り抜けるからです。
詳しく見ていきます。一般的な衛星の公転面は、母惑星の赤道面に一致していることが多いのですが、月の場合の公転面は地球の公転面 (黄道といいます)に対して約５度傾いています(天文年鑑では１９９８年版以後この記述が抜けています)｡ 月の公転面や星座の間の通り道を｢白道｣といいます。白道が黄道面に対して傾いているとどうなるか図に書いてみました。
地球がＤの位置にいるときは、新月の月は黄道面(太陽の方向)より南にいますので、月は太陽の南側を通り抜けます。これでは日食になりません｡ 満月の時も地球の影がある黄道面より上を通過します。この時も月食にはなりません。
地球がＥの位置まで進んだとします。Ｈ点は月が黄道面を南から北に横切る場所です。このような場所を｢昇交点｣といいます｡ この場所は白道上でもあるし黄道上でもある場所です。新月は昇交点にあります。黄道上(太陽の方向)にありますので、日食が起こります｡ Ｉ点を考えてみます。月が黄道面を北から南に横切っています。｢降交点｣といいます。満月は地球の影のできる黄道上にありますので､ 月食となります｡ 昇交点が太陽の方向を向くときに日食や月食が起こります。
地球がＦ点にいるときはＤ点同様日食・月食が起こりません。Ｇ点に来ると再び日食・月食が起こるようになります。降交点が太陽の方向 (昇交点が太陽と反対側)を向いたときも日食・月食が起こります。
まとめると次のようになります。日食・月食が起こるのは昇交点や降交点が太陽の方向を向くときで､ １年に２回あり、日食・月食は半月ずれてほぼ同じ頃に起こります。
４．日食・月食は毎年同じ時期に起こるか
ところで、もう一度３番目の図に戻って考えてみます。満月・新月の月の位置では、太陽からの引力の大きさがわずかに違います｡ そのために潮汐力が働きます(潮汐力についてはここを参照してください)。潮汐力は新月の時は太陽の方向､ 満月の時は太陽と反対の方向に働きます。
Ｄ点の地球・月を見てください。新月の時の潮汐力は太陽の方向です。この力は２つの力に分けて考えることができます｡ 一つは月の公転軌道を太陽の方向に引き伸ばそうとする力、もう一つは新月を黄道面に引き寄せようとする力です。前者の力は､ Ｅ点に来たときには引き伸ばそうとする方向が直角方向にずれますので、月が公転する間に打ち消しあってなくなります｡ ここで問題になるのは、後者の力です。黄道の方向に引き寄せられるのですから、月の軌道が黄道面の方向にずれます。昇交点の位置もずれ､ 予定よりの手前側になります。
昇交点通過後満月に達するまでは、潮汐力は太陽と反対向きに働き、月を黄道面に引き寄せる力として働きます。その結果､ 昇交点に達するまでと逆順の動きで満月になります。新月−昇交点が短かったのと同様に昇交点−満月間の距離が短くなります｡ 満月の位置も予定より手前側になります。同様に降交点、新月の位置も手前側になります。
(文章では、新月・満月と書いていますが、正しくは昇交点・降交点の中間地点のことで､ 月が軌道上で最も南や北にずれる地点のことをいっています)
全体としてみると、月の公転面の傾きの方向が手前側に回転していきます。これは黄道を北側(上)から見ると右回り(西回り) にまわる方向です｡ 昇交点の方向(昇交点黄径といいます)も西回りにまわっていきます。
ＥやＧの位置では、新月・満月が黄道面上にあるため黄道方向に引き寄せる力はなく、新月の時には潮汐力が働かないため､ 月の公転面の傾きの方向を回転させません。Ｆの位置ではＤと同様、月の公転面の傾きの方向を西回りに回転させます。
ちょっとわかりにくいので、違う考え方をしてみます。月の公転を、黄道面に沿う運動と垂直な方向の運動に分けて考えてみます｡ 太陽の影響がない場合、月の運動は地球の引力だけで決まりますので、黄道面に沿う運動と垂直な方向の運動の周期は同じです｡ でなければ一周すると同じ所に帰ってきません。ところがＤ点にいるときは、黄道面に垂直な方向の運動には、太陽の潮汐力が加わるので､ その分だけ地球の引力が強くなったように振る舞います。引力が強くなるとその分だけ回転が速くなります (実際には上下往復運動なので振り子の振れ方ににます)。回転が速いと周期が短くなります｡ 黄道に沿う運動では、太陽の影響を受けませんので、周期は変わりません。結局１周する前に、昇交点・降交点に戻ってしまいます｡ 周期が少なくなる分だけ、昇交点・降交点が手前側(西側)へ移動します。
１年の間では、公転面の傾きの方向(昇交点黄径)が西回りに回転します。西回りに回転した昇交点の延長が太陽を指すのは図ではＥ点の手前になります｡ １年に達する前に日食月食の起こりやすい時期がやってくることになります。そのため２０１１年のように、１・６･ １２月と年に３回も月食が起こるという年ができます。
昇交点の方向が太陽を指してから、再び同じになるまでを｢１食年｣と言います。１食年の長さは３４６.６２０１日で､ １年より約１９日短くなっています。日食月食の起こる時期は毎年２０日ずつ早くなります。
<参考文献>戸田盛和著「コマの科学」岩波新書 １９８０年
５．日食と月食の頻度
どちらがよく起こるかは、日食が起こるときの月の位置と月食が起こるときの月の位置を比べ、どちらが広いか考えればわかります｡ 図は少し正確にしましょう。地球の大きさは月の大きさの約４倍です。月が作る本影錐の頂点は､ 地球上で皆既日食が見えたり金環日食が見えたりするので変化しますが、ほぼ、地球上に来ると考えます。図を書いてみました(下図)。
左側１から３の番号をつけた月に注目します。太陽側にありますので、日食を起こす月です。３番の月は､ 球の中心に本影錐があたるように書いています。１番の月は、半影錐の端っこが地球にかかろうとしています。もう少しだけ地球側(３番側) によれば、北極か南極で部分日食が見られることになります。この位置が部分日食が起こる境界になります。３番からの月の中心の位置のずれは､ 月の３個分の大きさ、約１.５度になります。２番の位置よりほんのわずかだけ地球側によれば、本影錐が地球にかかります｡ どこかで皆既日食が見られることになります。実際には、地球の位置がこれより月に近かったり遠かったりしますので､ 地球上に本影錐が落ちていることになり、２番の位置でもじゅうぶんに皆既日食や金環日食が観察できます。この位置は３番の位置から月２個分､ 角度で１度離れています。
今度は右側４番から６番の番号をつけた月に注目します。６番の月は完全に本影に入っていますから、皆既月食になっています｡ ３個並んでいますので、月の中心が本影錐の中心から月１個分(０.５度)以内にいる必要があります。５番の月は本影に接しています｡ ほんの少しだけ本影側によれば部分月食になりますので、部分月食を起こす境界といえます。この位置は､ 月の大きさ２個分(１度)の大きさだけ本影の中心から月の中心がずれています。さらに外側の４番の月では半影錐に接していますので､ 半影月食を起こす限界になります。月の中心が本影錐の中心から月の大きさの３個分(１.５度)離れています。
このように考えてみると、皆既月食が起こる可能性が一番低く幅は約０.５度、地球上のどこかで皆既日食か金環日食が起こっている可能性と､ 部分月食以上の月食が起こっている可能性がほぼ同じで１度、地球上のどこかで部分日食以上が見られる可能性と､ 半影月食が起こる可能性はほぼ同じで１.５度となります。結局、日食と月食が起こる可能性はほぼ同じといえます。
１００年間に起こる日食・月食の回数は、金環日食・皆既日食が合計１５３.７回、月食は皆既月食７１.６回、部分月食８２.７回で、 合計１５４.３回だそうです(出典：天体観測ハンドブック)。だいたい同じような数値になっていますね。
次に、昇交点や昇交点が太陽を向く前後何日以内に月が通過すれば日食・月食になるか考えてみます。
右側の４の位置からスタートしたとします。半影月食が起こっています。その後、月が１公転して再び４に戻ってきたとき､ 地球の影はどこにあるでしょうか。白道の傾きは約５度ですから、図で１だけ上がると１１だけ左にずれます｡ ４から５までたてに０.５度ですから横に５.５度になります。縦線１本分左にずれるのに５.５日かかることになります｡ ４から左側の５まで進むのに２７.５日、左側の４まで進むのに３３日(月がこの区間を動くのにも１日かかる)かかります｡ ２７日では月は１周してくることはありませんから、半影月食どうし以外で満月が２回連続して月食になることはありません。
半影月食と部分日食が起こる可能性が同じですので、部分日食が連続した新月に起こることもあります｡ 皆既日食や金環日食が起こった前後の新月は日食となることはありません。
皆既月食と皆既日食(金環日食)の組み合わせはどうでしょうか。右側６の位置で皆既月食が起こったとし､ 左側５の位置(の真後ろ) で皆既日食が起こることは考えられます。この間１６日半で半月より１日だけ(月が右６から左５へ追いつく半日を引いています) 長いので、皆既日食皆既月食が連続して起こる可能性もわずかにあります。
当然のことですが、日食は影の中に入らないと見えない現象です。地球上で太陽の見える位置にいても、日食が見えないことがあります｡ これに対して、月食は起こっていて月が昇っていれば(昼間でなければ)必ず見えることになります｡ 従って見える機会としては月食の方が多いことになります。
６．日食・月食は予報できるか
現在では、太陽や月の運行のようすがはっきりわかっており、いつ日食や月食が起こり、どこでどのように見えるかも計算で求められています｡ それでは、昔の人はどうだったのでしょうか。太陽と月の位置を正確に観測しそこから月と太陽が重なるかどうかを求めることはできたようです｡ 何年も先のものまでというのは無理だったかも知れません。
(1)サロス周期の発見 日食・月食の起こり方には不思議な規則性があることが大昔から知られています。それについて考えてみることにします｡ 規則性を見るために１９７２年から２０２０年までの各年の何月何日に日食・月食があるかをまとめてみました｡ ８６年をのぞく７２年から２０１０年までは各年の天文年鑑から、２０００年から２０２０年までは国立天文台の暦計算室のサイト (http://eco.mtk.nao.ac.jp/koyomi/)から､ ８６年は天文シュミレーションソフトで求めています。
表中以下の記号を使っています。 K;金環日食 T;皆既日食 H;金環皆既日食 P;部分日食 t;皆既月食 p;部分月食 h;半影月食 年|1...2....3....4....5....6....7....8....9....10...11...12月 72 K t| | | | | |T p| | | | | K 73K h | | | | | h T|h | | | | |p K| 74 | | | | p T | | | | | t| P | 75 | | | |P t | | | | | P t | | 76 | | | K|p | | | | | T | | | 77 | | p K | | | | | |T | | | 78 | | t |P | | | | | t P | | | 79 | T|p | | | | | K |t | | | | 80 | T h | | | | h| K h| | | | | 81 h K | | | | | p T| | | | | | 82 t P | | | | | P t P | | | | | P t| 83 | | | | | Tp | | | | | K | 84 | | | |h K| h | | | | | K |h | 85 | | | t P | | | | | t|T | | 86 | | |P t | | | | | K t | | | 87 | | H| h | | | | | K |h | | | 88 | p T | | | | | p|K | | | | 89 | t |P | | | | | t P| | | | | 1....2....3....4....5....6....7....8....9....10...11...12月 90 K| t | | | | | T |p | | | | | 91 K h| | | | | h|T h| | | | | p | 92 K | | | | | p T| | | | | |t P | 93 | | | | P t | | | | |P t| | 94 | | | |K p | | | | | T h | | 95 | | |p K| | | | | h T | | | 96 | | t P | | | | | t|P | | | 97 | |T p| | | | | P t | | | | 98 | T| h | | | | |h K |h | | | | 99 h| K | | | | | p| T | | | | | 00 t P | | | | P t P| | | | | P| 01 t | | | | | T p | | | | |K h| 02 | | | | h| K h| | | | | h T | 03 | | | | t K| | | | | |t T | | 04 | | | T p | | | | |P t| | | 05 | | H h | | | | | K p | | | 06 | | h K| | | | | |p K | | | | 07 | t P | | | | | t| P | | | | 1....2....3....4....5....6....7....8....9....10...11...12月 08 |K t | | | | | T p | | | | | 09 K|h | | | | | T |h | | | | p 10p K | | | | | p| T | | | | | p P 11P | | | | P t P | | | | P|t | 12 | | | | K p | | | | |T h| | 13 | | | p|K | | | | | h H | | 14 | | |t K| | | | | |t P | | | 15 | | Tt | | | | |P t| | | | 16 | |T h| | | | | K h | | | | 17 |h T | | | | | |p T | | | | | 18 t P | | | | | P t| P | | | | | 19 P t| | | | | T p | | | | | K| 20 h | | | | |h K| | | | | h|T |毎年、日月食の起こる時期が早くなっているのは、１食年が１年より短いからです。そのずれが大きくなって再び元の位置に戻るまで､ １８年かかっています。その１８年で、何月かを示す目盛りをわざと入れて区切っています。この区切りに囲まれた部分に注目してください｡ わずかに右にずれていくものの同じパターンが繰り返されているのに気がつきませんか。たとえば真ん中くらいにＴｐと並んでいて､ その下の段はｈＴｈその下はｐＴと並んでいます。１９９０年から、２００８年からを見ても､ ｈがなくなったりｐに変わったりという変化がたまにあるものの同じ文字の並びが繰り返されています｡ 日月食のパターンが明らかに読み取れます。古代バビロニアやギリシャでもこの繰り返しがあることが知られていました｡ 現代ではサロス周期と呼んでいます。
(2)サロス周期の不思議 サロス周期がどうしてできるか考える事にします。まずサロス周期を求めます。１８年は６５７４.３５９６日(365.2422*18)あります｡ 日食は新月の時にしか起こりません。したがってサロス周期は新月になる周期の倍数になります。新月から次の新月までの長さは１朔望月といい､ ２９.５３０５８８９日あります｡ 先ほどの日数をこの数値で割って２２２.６。これより少し大きな整数の２２３が､ サロス周期の間に朔望月が繰り返される回数になります。従ってサロス周期は６５８５.３２１３２日になります｡ １８年の内に閏年は３〜５回あります※１ので、サロス周期は１８年と１０〜１２日と７時間４３分(約８時間)になります。
サロス周期には不思議な一致がいっぱい見られます。例えば月が昇交点を通過してから次に昇交点を通過するまでの日数を考えてみます｡ この日数を１交点月といいます。昇交点に月が来ないと日月食が起こりませんので交点月は非常に大事です｡ １交点月は２７.２１２２日あります｡ ２４２倍すると６５８５.３６日になります。また、月は地球に近づいたり遠ざかったりしています｡ この周期は１近点月といい､ ２７.５５４６日です。２３９倍すると６５８５.５４日です。地球に近づく遠ざかるは､ 金環日食になるか皆既日食になるかの要素として大事です｡ 最後に食年の長さです。これも１９倍すると６５８５.７８日になります｡ 日月食が起こるかどうかが決まる周期の倍数どれもが６５８５日になるという奇妙な一致が見られます※２。整理してかきます。
(データは天文年鑑２００８年版使用)
1 朔望月 = 29.5305889日 223 朔望月 = 6585.32132日 新月(満月)になる周期
1 交点月 = 27.2122209日 242 交点月 = 6585.35745日 昇交点を通過する周期
1 近点月 = 27.5545498日 239 近点月 = 6585.53740日 近地点を通過する周期
1 食 年 = 346.620079 日 19 食 年 = 6585.78151日 昇交点が太陽を向く周期
何回繰り返すかという数値に注目すると、２４２以外は素数で、そうでない２４２(11*11*2)もその他の数値とは共通の約数を持ちません｡ サロス周期の中では、日月食の度にそれぞれの周回数を求めたときに少数以下の値が異なります。そのため、サロス周期内では､ 毎回欠ける大きさや方向､ 見られる地域が変わります。
※１ １８年間の閏年の回数
２０００〜２０１７年だと2000,2004,2008,2012,2016年の５回
２０９７〜２１１４年だと2104,2108,2112年の３回
※２ 実際には、朔望月の倍数(サロス周期)と交点月の倍数とが完全に一致しているなら､ 食年の倍数も完全にそれに一致するはずです。例えば昇交点上に月がいて、その延長上に太陽が来た時(日食が起こっている)を考えます｡ サロス周期後には、何朔望月かが過ぎていますから、新月になっています。このことから月の延長上に太陽がいることがわかります。また､ 何交点月かが過ぎていると仮定しましたので、月は昇交点に戻ってきています。これを３段論法で考えると､ 昇交点に月がいる＋月の向こうに太陽がいる→昇交点に太陽がいる という図式になります。昇交点に太陽がくる周期が食年で､ 何回あったかはわかりませんので何食年かが経過していることになります。食年の倍数が一致するのは当然といえます。
(3)日食家族 サロス周期を経た後に起こる日食はよく似た形で起こります。これらをまとめて１つの系列とする考え方ができます｡ 例えば、先ほどの日月食の発生日を書いた表では、１９７２年１月中旬の金環日食と１９９０年１月下旬の金環日食､ ２００８年２月上旬の金環日食は同じ系列に属すると考えます。これらの日食は非常によく似た形で起こっています｡ １９７２年から１９８９年までの間には、日食は３９系列あります。１サロス周期の中でも系列の数は増減します｡ 例えば２０１１年７月１日に起こった部分日食の１サロス前にあたる１９９３年６月中旬には日食が起こっていません｡ 新しい系列が加わったことになります。この場合、６月２日の日食と親子関係として同家族にします。各食年の､ 昇交点で起こる日食(昇交点日食)、降交点で起こる日食(降交点日食)を一つ一つを日食家族として扱い、新たにできた日食の系列は､ 家族内の子どもとして扱います。１サロス周期は１９食年ですので、日食家族は３８家族になります。新たに子どもができ続けていくと､ 日食がいっぱい起こるように見えてきます。実際には、子どもができた家族はしばらくすると親が日食を起こさなくなります｡ その理由は次で説明します。
昇交点日食か、降交点日食かは表からは区別できません。その日食とその前後に起こる皆既月食との組み合わせで考えます。例えば､ ２００７年には３月４日と８月２８日の２回皆既月食があります。それぞれの直後の３月１９日、９月１１日に部分日食が起こっています｡ ３月のは北半球で、９月のは南半球で見られましたので、３月は昇交点日食、９月は降交点日食になります｡ 同じ帯上にある日食は同じ種類になります。従って、２００９年７月２２日トカラ列島で見られた皆既日食は､ ２００７年９月の日食と同じ帯上にありますから降交点日食となります。
月食にも同じように考えると家族があるはずですが、月食家族という用語はあまり使われていないようです｡ 日食に比べて影の中心帯がわかりにくく、月食の違いがわかりにくいからでしょう。もちろん、昇交点月食・降交点月食はあります｡ 昇交点日食と帯が重なっているのが降交点月食です。
(4)サロス周期内で日食の起こり方がどう違うか サロス周期が、一致するといっても、微妙にずれがあります｡ この影響を考えてみます。その前に、サロス周期そのものに、少数以下の端数があります。これからどういう事が起こるのでしょうか｡ 単位は日ですので、１日の長さとは同期していないことを示しています。つまり、少数以下の約３分の１日の端数があることによって､ たとえばある日の正午に日食が起こったとすると、１サロス周期経過後の日食は午後８時に起こることになります。夜ですので､ この日食を見ることはできません。実際に見ることができるのはこの時間帯が昼間のところ、地球上の経度で１２０度西側の地域になります｡ 日食が起こる時間は遅れ、見られる地域が西にずれてくるのです。ところがこれも偶然なのですが、３サロス周期後になりますと､ 地球を１周してほぼ元の位置に戻ってきます。５４年後には、再び日月食が見られることになります｡ 正確にはサロス周期の小数部の３倍は１に０.０３６、時間にすると５２分だけ不足しています｡ その分、経度で１３度東にずれることになりますが、ほとんど同じ地域見られると言っていいでしょう※｡ ３サロス周期後は、１年の長さより１ヶ月ほど長く、起こる月が遅れていくことなりますが､ 日食の周期に何らかの影響を与えるものではありません。
※１３度東にずれるのは、太陽(月)から見て、地球の真ん中に見える地点(地上で太陽が頭上にある地点)の経度です｡ 一つの子午線(例えば東経１３５度)が、地球の真ん中に見えるようにしながら地球儀を回してみると、地球(上の各地点) が上がったり下がったり回転したりするように見えます。その影響で、以前より東側に影が落ちても、西側の地点が影に入る (日食になる)こともあります。
(5)日食家族の世代交代 １サロス周期と２４２交点月の間にも３０分の１日ほどの差があります。足りません｡ 昇交点で起こった月食があったとします。次の回では、月がまだ昇交点に達していないことになります｡ 昇交点の手前側は黄道より南ですので、月が地球の影の中を横切る位置がわずかに南へずれます。サロス周期が来るごとにずれ､ そのずれが大きくなればそのうちに影を横切らなくなります。時代をさかのぼれば、北の端を横切る半影月食に始まって､ 部分月食、皆既月食へと変化してきました。日食も同じように、北極をかすめるものから始まり、次第にその中心線が南下していき､ 南極をかすめるようになって日食が見られなくなります。降交点で起こる日月食の場合、動きの向きはこの逆で、南から北へ移り変わっていきます。
日食家族の１系列が起こす日食について考えてみます。１サロス周期と交点月の不足分は、角度で０.４８度(３６０×不足分÷交点月の日数)あります｡ 皆既日食を起こす範囲は約２２度(月が地球の影を横切る図を参照)ですから、４５回ほど繰り返すことになります。年数で８５０年になります｡ またその前後それぞれ１１回(２００年)ほど部分日食を起こします。
日食家族には１２００年ほどの寿命ができることになります。尽きればどうなるのでしょうか｡ 昇交点日食の寿命が尽きる直前を考えてみます。この頃には月がずいぶんと南によっています。月が地球を横切る図では､ 右側の４に近い位置に相当します。ここで日食を起こしたときは、次の新月の時には左側の４に相当する位置に達していません｡ ３と４の間に相当する位置にいますので、部分日食を起こしています。新しい日食系列が生まれたことになります｡ この一つの例が先に述べた２０１１年７月の日食です(降交点日食ですが)。降交点日食では図の上下(南北) が入れ替わるだけで、全く同じ現象が起こります。
子どもができて、しばらくすると親がなくなるということを繰り返して日食家族が受け継がれていきます｡ この現象を日食家族の世代交代といいます。これに従えば、親も子も同じ家族なので、同じ日食家族に含めて考えることになります｡ 世代交代は交点月(食年)の不足分を解消する方法ですので、それから考えても、親と子は同じ家族に入れて考えるのが正しいでしょう。
参考になるサイト 日食とサロス周期 http://www.hucc.hokudai.ac.jp/~x10553/guide/guide.html
解明できていないこと
３サロス後の日食の見られる位置がどのように見られるか(数式ばかりになるので解明できても簡単には解説できないと考えられる)
日食家族の寿命が一定でないこと
７．天体の食・掩蔽現象
一般に○○食と言われるものは、ほとんどが掩蔽現象です。食は影に入って見えなくなる現象ですので､ 自らが光っていない惑星や衛星のような天体だけに起こります。あまり厳密に考えずに、掩蔽も含め食としてどの様な現象があるか､ それから何がわかったのかをまとめることにします。
食・掩蔽現象を観測できるのは、ほとんどの場合、星を観測していて急に暗くなった、突然明るさが戻ったというような現象として観察されます｡ いつ、どれくらい明るさが変わったかということを正確に記録できるようにすることが大切です。影が見えているわけでもないし､ 場合によっては星そのものも光がその方向からやってきているというだけで、形や大きさがわからないこともあります。
(1)人工衛星の食
人工衛星は、日没後や日の出前に何個か見られることがあります。ふつうは、地平線から上って、地平線に沈んでいくのですが､ 中には、空に突然現れたり、急に消えたりするものもあります。これは、地球が作る影に入ったり、影から出たりするからです。
静止衛星などで問題になるのは、春分や秋分の頃の真夜中に地球の影に入ることがあります。太陽電池で発電できなくなりますから､ 運用が休止されることがありました。最近では、電池などを使うことによってそのようなことがなくなっています。気象衛星ひまわりで､ 画像の配信がなくなるのは、影にはいるというより、太陽が写り込む事が問題なので、これを避けるために休止することがあります｡ http://mscweb.kishou.go.jp/panfu/operation/reference/equinox/index.htm
(2)木星やガリレオ衛星による食・掩蔽
惑星の周りを回る衛星でも、惑星との間で食や掩蔽を起こします。木星の４大衛星(ガリレオ衛星)は双眼鏡でも観察できるので､ 木星の影に入ったりする(木星に食される)のが観察できます。実際には木星本体とずれた位置で、突然消えたり、出現したりします｡ この現象はしばらく観察し続けていないと確認できない現象です。例えば、下の図は､ １９９０年１月の２３日２５日２７日の３日間１時間おきに撮影した木星とガリレオ衛星の写真です (反転していますので、黒いところが衛星や木星になります)。中央の大きな黒円が木星本体で､ 衛星には内側のものから順に番号をふっています。ここで１をつけた第１衛生イオの公転周期は１.７７日ですので､ ２３日２３時１５分と２５日１８時ちょうどには、木星に対してほぼ同じ位置にいます。そう考えて図をよく見ると､ ２５日２０時ではイオがいるはずのところに写っていないことがわかります。木星に食されているのが原因です。それ以前の､ １８時１９時は木星の向こう側にいますので、掩蔽されていて写っていません。
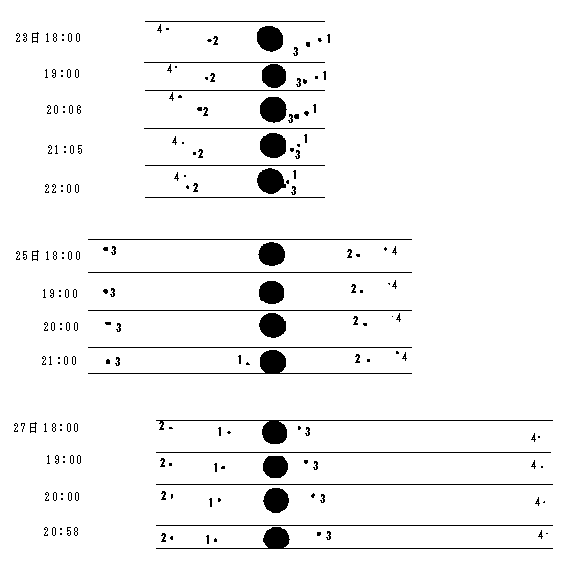
木星の衛星が木星の向こう側を通ればこのようになります。今度は手前側を通るときを考えてみます。木星の手前側を通り抜けるわけですから､ 木星の面に重なって衛星が見えます。衛星が木星を隠しているのですが、木星の方が大きすぎて隠しきれません。このような場合､ 掩蔽といわずに衛星の木星面｢通過｣といいます。また、衛星の影が木星面の上に落ちて黒い点になって見える場合もあります｡ これを見るのには、少し大きめの望遠鏡が必要です。
ガリレオ衛星の公転面の昇交点の方向(昇交点黄径)と、太陽から見た木星の方向(日心黄径)が同じになると(正反対になるときも)､ 地球に日月食が起こるのと同じ理由で、ガリレオ衛星どうしで隠したり隠されたり(掩蔽)、影に入れたり(食)といった相互現象が起こります｡ 衛星の大きさや明るさ、運動の方向が複雑に変化しますので、起こったときの起こり方やその程度、継続時間は微妙に変化します。この現象は､ ２００９年１月から２０１０年４月に、その次は２０１４年８月から２０１５年８月にありました｡ 木星の公転周期の半分である約６年ごとに起こります。
 ガニメデの影 |
 ガニメデ木星面通過 |
 木星衛星の相互食 |
(2')土星の衛星の食(食・掩蔽)
木星の衛星の公転面と木星の公転面とはわずかに傾いているだけなので、木星とガリレオ衛星間の食掩蔽は１年を通してみることができます｡ これに対して、土星の衛星の公転面と土星の公転面は３０度近く傾いているので、地球と月との間で日月食が起こるときと同じ様な関係になって､ 初めて起こります。この時、地球から見ると土星の輪は真横から見ることになり、非常に細くなり、場合によっては全く見えなくなることがあります｡ 例えば２００９年９月４日に輪がみえなくなりました｡ この前後１年間に土星と衛星の間での食・掩蔽が起こっています。衛星相互の間での食・掩蔽も起こっていますが､ 土星の衛星ではテイタン以外は暗く観測には中〜大型の望遠鏡が必要でした。
土星の輪に土星の影が写っていたり、土星本体に輪の影が写っていたりすることがありますが、明るさの変化として観測することはないので､ これを食現象とした記録はありません。
 環の消えた土星 |
 土星(環に影) |
(3)星食(掩蔽)
月が太陽を隠して日食を起こすように、月が星を隠して見えなくする事(掩蔽)があります。この現象を星食といいます｡ 隠す星が恒星の場合恒星食といい、惑星の場合は惑星食といいます。
星が隠されても、昼間では見えません(望遠鏡を使えば１等星は見えるかも)ので、観測できません。また、月が沈んでいてもだめです｡ 新月の前後は星食が観測しにくいといえます。逆に満月の前後は、月明かりが強くて星が見づらくなります。観測できる星食は限られてきます｡ 上弦月の頃は、暗い縁から星が隠れ、明るい縁から現れます。下弦の月ではこの逆となります。
月の通る白道はほぼ黄道に沿っていますので、ほぼ黄道沿いの恒星が隠されることになります※１。例えば１等星では､ さそり座アンタレス､ しし座レグルス、おとめ座スピカがその対象となります。おうし座アルデバランも隠されることがありますが､ 地球上の地域によっては､ その現象が全く起こらない場所もあります｡ 変わったところでは、すばるやプレセペといった星団も隠されることがあります。
 スピカ食２０１３年８月１２日 |
 すばる食２００９年９月１１日 |
 すばる食２００６年１１月７日 |
１年単位で見ると白道はほぼ決まった位置にあります。隠される星はほぼこの線上にあるときだけです。１年のうちでは､ 毎月同じ星の近くを月が通ることになり、黄道近くの星でも隠されないものが出てきます。しかし､ 白道に注目してみると先に述べた昇交点の移動によって少しずつずれていきます。何年かすると違う星の近くを通ることになります｡ そして昇交点が１回転すると、また元の星の近くを通るようになります。昇交点は１８.６年で１周します※２ので、その間に､ 食が続く時期は１回または２回あります。例えば、すばる食は２００５年から２０１０年にかけて起こっていましたが､ その後しばらくは起こらなくなり、次に起こるようになるのは２０２３年です。
星食を観測することによって、月の運動のようすを調べたり、地球の自転のようすなどが詳しくわかります｡ 最近では、レーザーで月までの距離を測ったりといった方法でより正確にわかりますから、星食から求めるということはなくなってきました｡ どちらかというと星の位置精度の向上に使われているようです。
星が月の南または北の縁ぎりぎりを通る現象を接食といいます。月の山や谷の形によって星が現れたり消えたりします｡ これによって、月の表面のでこぼこのようすが詳しくわかります。これも｢かぐや｣などの探査機による測定データから知ることができ､ 二つのデータを比較検討してるところです。
(3')惑星食 惑星食は、相手の天体によって呼び方が変わります。恒星食に比べると起こる回数は少ないようです｡ 惑星は恒星より明るいことが多いので見応えがあります。
 水星食 |
 金星食 |
 木星食 |
 土星食 |
 月と土星 |
 月と土星 |
※１ 白道は黄道に対して５.１５度傾いていますから、月は黄道の南北両側この角度の範囲を通ります｡ また月は最大で半径０.２８度の大きさに見えますので、この範囲の星を隠すことができます。地球上で月の南中時高度が０度の地点では､ ９０度の地点に比べて月の位置が最大で１.０４度ずれて見えます(視差)。これらの要素を最大限に見積もると､ 黄道の南北６.４７度の範囲が地球上から見て星食が起こる可能性のある範囲となります。
※２ 昇交点が１周する周期は、１食年の逆数と地球の公転周期の逆数との差を計算し、その逆数を撮ることで求められます｡ この計算式は、惑星の会合周期を求めたり地球の自転周期を求めたりするのと原理は同じです。
(4)惑星による恒星食(掩蔽)
惑星も恒星を隠すことがあります。この現象を観測しているといろいろなことがわかることがあります。
１９７７年３月１０日に天王星が恒星を隠しました。見ることができたのは南インド洋と南極大陸だけだったのですが､ この時恒星が隠れる３０分ほど前に５回わずかに星が暗くなりました。そして、再び天王星から出現した後､ 先ほどと逆の順番でわずかに星が暗くなりました。この現象は、天王星に５つの輪があり､ それによって恒星の光が弱められたために起こったと考えられました。天王星の輪については発見者であるハーシェルが､ 輪が見えるといっていたのですが、当時の望遠鏡では観測不可能であるし、以後の観測でも見つからなかったので誤りとされていました。
小惑星も恒星を隠すことがあります。小惑星による恒星食では、恒星より小惑星の方が暗いことが多く､ 恒星が暗くなるようすから小惑星に隠されたと判断できます。恒星が隠れ暗くなっている時間から小惑星の大きさがわかります｡ 望遠鏡では小惑星の大きさは測定できないのですが、この方法で大きさを、何地点での観測をあわせることで形､ あるいは衛星があるといったことまでわかります。薩摩川内宇宙館を中心に精力的に観測されています｡ http://sendaiuchukan.jp/data/occultshort.htmlに詳しく書かれています。
(5)日面通過(惑星による太陽の掩蔽)
地球より内側をまわっている水星・金星は太陽の前を横切ることがあります。水星・金星は太陽に比べて非常に小さく､ 太陽の表面上を真っ黒な点となって移動していきます。この現象を日面通過といいます。水星や金星の公転軌道は､ 地球の公転軌道に対して傾いていますので、内合や外合の度に起こりません。昇交点や降交点上に惑星・地球がいるときのみ起こります。
(5a)水星の日面通過 太陽の前面を水星が横切る現象です。
 1993年11月６日 |
 2006年11月９日 |
水星軌道の降交点や昇交点の延長上に地球が来るのは、５月８日と１１月１０日頃です｡ 水星の日面通過が起こるのは毎回この前後数日の間に内合になるときです。
水星の会合周期は１１５.８８日です。４１会合周期が１３年＋約３日、１４５会合周期では４６年−１日です｡ 従って一度日面通過が起こると、その１３年、３３年、４６年後に日面通過が起こる可能性が高くなります。
水星の軌道はだ円形ですから、水星は太陽から遠ざかったり近づいたりします。５月頃は遠日点付近にいます。内合の頃の水星は､ 地球に近づきます。距離が近いと見かけの速さは早くなりますので、日面通過となる区間を早く通過します。そのため水星の日面通過は､ １１月より５月の方が少なくなります。１９７０年から２１１１年に日面通過が起こる(起こった)日は次の通りです。 ()内の数値は間の年数です。規則性が読み取れたでしょうか。
５月 * １１月
1970/05/09 * 1960/11/07 --+
| (33)* | (13) | (33)
| * 1973/11/10 |
| * | (13) |
| * 1986/11/13 |
| * | (13) V
| * V 1993/11/06
V * 1999/11/15 | (13)
2003/05/07 * 2006/11/08 --+
| (13)* | (13) | (33)
2016/05/09 * 2019/11/11 |
| (33)* | (13) |
| * 2032/11/13 V
V * 2039/11/07
2049/05/07 * | (13)
| (13)* 2052/11/09 --+
2062/05/10 * | (13) | (33)
| (33)* 2065/11/11 |
| * | (13) |
| * 2078/11/14 V
V * 2085/11/07
2095/05/08 * | (13)
| (13)* 2098/11/10
2108/05/12 * | (13)
* 2111/11/14
(5b)金星の日面通過 金星軌道の昇交点・降交点の延長上を地球が通過するのは、６月７日と１２月９日です｡
金星の日面通過はこの前後に内合になったときに起こります。また会合周期は５８３.９２日です。５会合周期が８年に２日不足､
１５７会合周期が２４３年に０.１日余分ですので、一度起こるとその８年、２４３年、(２５１)年後に起こる可能性があります｡
以下が金星食のおこった日、起こる予定の日です(１８７４年から２４９８年まで 年／月日で記入しています)。基準日 ８年後 243年後 251年後 486年後 494年後 2004/0608 2012/0606 2247/0611 2255/0618 2490/0612 2498/0609 1874/1209 1882/1206 2117/1210 2125/1208 2360/1212 2368/1210１６７９年にハレーは、金星の日面通過を観測することによって地球太陽間の距離が測定できるといいました｡ 惑星の運動の観測から、地球の公転半径に対する惑星の公転半径の比(何天文単位か)はわかるのですが､ 地球の公転半径を測定する手段がありませんでした。地球上の各地での日面通過時刻がわかれば､ その違いを視差として利用することによって金星までの距離が求められ、そこから地球の公転半径が導き出されます｡ １７６１年１７６９年の金星の日面通過で精密に観測され、地球太陽間の距離が明らかになりました｡ 現在ではレーダーなどで惑星までの距離を直接測っています。
参考文献 天体観測ハンドブック 天文年鑑２００４年版 誠文堂新光社
(6)食変光星
連星の中で、太陽(地球)からみて恒星の回転面が真横になっているとき、連星の恒星どうしが互いに隠したり隠し合ったりします｡ このとき、星は暗く見えますので、周期的に明るさが変化します。これが原因で、明るさが変化する星を食変光星といいます｡ 恒星が非常に遠くにあって、二つあるのが望遠鏡で見えない場合でも、恒星が２つあることがわかります。また､ ドップラー効果を利用した運動速度の測定もあわせて計算することで、両星の質量や直径を求めることができます｡ 食変光星は、二つの星の大きさ、性質などによって明るさの変化の様子が違います。変光のようすから、恒星の性質もわかります。
最近ではトランジット法といって、恒星の周りを回る惑星が恒星を隠す事によって起こる光度の変化が測定できるようになってきました｡ これを利用して、系外惑星が発見されています。実際には太陽に木星サイズの惑星があるとして考えてみます｡ 木星の大きさは太陽の１０分の１ですから面積は１００分の１になります。遠くの星から見て、太陽の前を木星が横切ったとしても､ 明るさは１％暗くなるだけです。明るさの測定はかなり正確に計る必要があります。
８．日食・月食の用語
(1) 日食の見られる地域：日食地図(日食図)
地図上に日食が見られる範囲を記入した図を日食地図といいます。日食図と書かれている場合もあります。図からは､ 地図上に表された地域では日食がどのように見られるかがおおよそのようすがわかります。図とともに考えてみます｡ 図は、国立天文台暦編纂室のサイト(http://eco.mtk.nao.ac.jp/cgi-bin/koyomi/eclipsex_s.cgi)で閲覧できます｡ このサイトの図を使って解説することにします。解説の都合上、経緯線・日本以外の海岸線を消去した(図の容量を小さくするためです)後､ 着色したものを使用します。実際には、解説で説明する線だけでできています。
ふつうの日食地図：何がふつうで、何がふつうでないかは決められないのですが､
地球上に月の影が完全に落ちている場合の日食地図を考えます。２００９年７月２２日トカラ列島で見られた皆既日食の時のものです｡
全体として鼓のような形になっています。地図の形式によっては多少違った形になります。真ん中を横切って赤く塗られた所が､
皆既日食の見られたところです。暦編纂室の図では北限界線、南限界線、中心食線(影の中心が通るところ)､
各時の影の輪郭が記されていますが、図では一色にしています。金環日食を表す図ではこの範囲が金環日食の見られる範囲となります｡
皆既日食では中程が太く、逆に金環日食では細くなります。そのほか青く塗ったところが部分日食の始まりと終わりが見られた所、水色が部分日食が見られたものの始めまたは終わりが見られなかった所です｡ 月の影の中心は、３時間半ほどかけて地球を西から東に横切っていきます。そのため、西(左)側の水色部がはじめが見られないところ､ 東(右)側が終わりが見られないところになります。何時にどのように見られるかは、別の表や図から判断する必要があります｡ 着色していないところでは、日食は全く見られません。
ここで、日食地図に書かれている境界線の意味と名称を整理しておきます。
青色区域の北側や南側の、塗っていないところとの境界線(桜色)は日食が見られる所と見られない所との境界線になりますので､ 日食北(南)限界線といいます。
その他の境界線は以下に列挙します
西側の水色区域の境界線は西側から順番に
黄土色：日の出と同時に欠け終わる所＝日出復円線(ふくえんせん)
黄橙色：日の出に最も欠けている所 ＝日出食甚線(しょくじんせん)
黄 色：日の出と同時に欠け始める所＝日出初虧線(しょきせん)
同様に東側の水色区域の境界線は順番に
紫 色：日没と同時に欠け終わる所＝日没復円線
マゼンタ：日没に最も欠けている所＝日没食甚線
藤 色：日没と同時に欠け始める所＝日没初虧線
初虧線と復円線はつながっています。その場所では欠け始めると同時に終了しますから、日食は一瞬の間だけ見られます｡ 月の半影の端がかすめて通る場所になりますから、日食北(または南)限界線と接しています。また､ 欠け始めと欠け終わりの真ん中に最もかける時刻がありますので、食甚線とも重なります。４本の線がこの１点からのびていきます。
北に偏った日食地図：地球が月の半影を部分的に横切るとどうなるのでしょうか。図は２０１２年５月２１日の金環日食のものです｡
日食北限界線がなくなり、東西にある日食が部分的に見られる地域がつながっています。日出復円線と日没初虧線、日出初虧線と日没復円線､
日出食甚線と日没食甚線とが北側でつながっています。それでは、それぞれの接点はどこになるのでしょうか。日出復円線と日没初虧線で考えてみます。接続点では、日の出と日の入りが同時に起こっています｡このようなことが起こるのは､ 北極圏内で夏なら北の地平線上を太陽がかすめて通る時、冬なら南の地平線上に一瞬だけ太陽が顔を出すときになります｡ 始まりと終わりが同時ですから、日食は太陽が地平線をかすめる一瞬だけ起こります。
この時を宇宙から見たとすると､ この位置は月の影が地球を通る最も北側の端になります。日食北限界線上にあるともいっていいでしょう｡ 日出復円線と日没初虧線の最も北側､ 言い換えれば高緯度側になる場所でつながっています｡ 北極に最も近づく所が線の変わり目といえます。日出初虧線と日没復円線､ 日出食甚線と日没食甚線についても､ 北極に最も近づく所が線のつなぎ目となります。
月の影の一部だけが地球の南半球を通過した場合、南北が逆になるだけで同じような日食地図ができます。
もっと北に偏った日食地図：２０１９年１月６日、日本で部分日食が見られるときのものです｡
本影が地球から離れたところを通過するため、皆既日食や金環日食の見られる地域がありません｡
冬に見られる日食なので北極(×印で示しています)から離れたところに日食の見られる地域があります｡
日出初虧線と日没復円線といった線どうしがつながっているのは先ほどの場合と同じです。この時期の日食地図では不思議なことが起こります。食甚線が初虧線や復円線から外側にはみ出しています｡ この場所では日食はどのように見えるのでしょうか。
食甚線上で考えてみます。日出食甚線と日没食甚線のつなぎ目で考えてみます。ここでは３つの現象が同時に起こっています｡ つまり、日の出とともに日食が最大になり、太陽は直後に沈んでいきます。この場所では、日食の始まりも終わりも見られないのに､ 日食を見ることができます。
このような、欠けた太陽が昇ってきて、欠けたまま沈んでいく場所は、図の線からはみ出した場所にあります｡ その場所は次の３本の線に挟まれた地域にあります。１つめは北極を中心として、日出復円線と日没初虧線との接続点､ 日出初虧線と日没復円線との接続点を端点とする円弧、２本目は日出初虧線、３本目は日没復円線です｡ この地域では最初から最後までというようにいかないけれど、日食が見られるということで図には水色 (本来の水色区域も水色です)に着色しています。
夏の日食では、これと逆のことが起こる地域があります。日食が始まってから太陽が沈み､ 終わりかけると太陽が昇ってくるという不幸？な地域です。２０１２年の日食地図では図に示せるほど広くはないので､ 記入していません。青く塗った地域の中にわずかですがあります。
日本で使う限り、日食地図は単純でわかりやすいものです。北極圏や南極圏、その近くの地域では読み取りに注意が必要な場合があります。
星食の見られる区域を示した地図も、日食地図に似たものになります。星食では、日食の見られる区域の幅が、月の太さで描かれます｡ 惑星による恒星食では、惑星の太さでになります。木星や土星などの場合はその方向さえ向いていれば見ることができます｡ 小惑星では、その直径と同じ幅で掩蔽帯ができます。
月食や日面通過は、月や太陽が出ていれば見られるので、開始時刻・終了時刻にその天体が出ている半球を示す図で描かれます。 この図も日食地図が変形したものと見なせます。
参考文献：天体観測ハンドブック 誠文堂新光社
(2)日食や月食の状態を表す用語
日食や月食時には、状態を表す数値が公表されており、そこからどのようになっているかを判断することができます｡ 例えば、２０１２年の金環日食の時の明石での予報は以下の通りになっています(国立天文台暦編纂室のサイトより抜粋しました)。
備考 |方向角[°] | 太陽° |視半径"| その他 /時刻 北極 極頂 天頂|高度 方位|太陽 月|角距離 食分 食始 | | | | 6:17:04|252 -58 310 |15.4 75.8|948 887|1835 0.000 6:40:00|251 -59 310 |20.0 78.7|948 888|1229 0.320 金冠開始 | | | 7:28:59|175 -61 236 |30.0 85.0|948 890| 58 0.939 食甚 | | | | 7:29:28|163 -61 224 |30.1 85.1|948 890| 57 0.940 金冠終了 | | | 7:29:57| 152 -61 213|30.2 85.2|948 890| 58 0.939 食終 | | | | 8:53:3 | 75 -60 135 |47.3 97.4|948 894|1842 0.000※部分食開始を第１接触、月が太陽に入りきった時(金環食開始)を第２接触、月の一部が太陽から出始めたとき(金環食終了) を第３接触､ 部分食の終了を第４接触といいます。皆既日食の場合、第２接触より先に第３接触が起こります。
それぞれの用語の意味は以下の通りです。なお、隠される天体をＡ、隠す天体をＢと表すことにします｡ 日食の場合Ａが太陽でＢが月に､ 月食の場合Ａが月でＢが本影または半影になります。
| 北極方向角 | Ａの中心を基準に、天の北極方向とＢの中心がある方向の角度を反時計回りに測った角度 |
| 極頂方向角 | Ａの中心を基準に、天の北極方向と天頂方向(上)の角度を反時計回りに測った角度※１ |
| 天頂方向角 | Ａの中心を基準に、天頂方向とＢの中心がある方向の角度を反時計回りに測った角度 |
| 高度 | Ａの中心の高度。地平線からの角度を用いる |
| 方位 | Ａの中心の方位。北から西回り(右へ：先に東を通る)に測る |
| 視半径 | 天体の中心から縁までの大きさ。角度で表す |
| 角距離 | Ａの中心とＢの中心との距離。角度で表す |
| 食分 | Ａの直径に対して、ＢがＡを隠す割合※２ |
| 北極方向角から天頂方向角を引いたものが極頂方向角になります。 ６時４０分の場合 北極方向角(251)−天頂方向角(310)＝極頂方向角(-59) | |
| ※２ | 二つの天体が重なっている幅は、２天体の半径の和から２天体間の距離を引いたものです。視直径は視半径の２倍ですから､
重なり幅を天体Ａの視半径を２倍したもので割れば食分が求められます。 ６時４０分の場合 重なり幅＝太陽の視半径(948)＋月の視半径(888)−角距離(1229)＝607 食分＝重なり幅(607)÷２÷太陽の視半径(948)＝０．３２０ となり、表の値と一致します。 金環日食中は入り込んだ月の後側の太陽は隠されていません。単純に考えると隠された割合は、月の視半径÷太陽の視半径になります｡ この場合、金環日食中の食分はほとんど変化しないことになります。実際には月が太陽の中にどれくらい入り込んでいるかを知りたいので､ 後側の隠されていない部分を無視することもできます。計算方法は上記の方法がそのまま使えます｡ どちらの方法を使っているか注意する必要があります。 |
実際にデータを使って作図してみます(右図)。まず、どれくらいの長さをどれくらいの大きさで表すかを決めます。その大きさに従って、図の中央に太陽を書きます｡ 太陽の中心から図面上方向に線を引き、これを実際に見たときの上(天頂)方向とします。
６時１７分４秒(部分食開始時刻)の月の位置を書いてみます。太陽の中心の位置で､ 上方向から反時計回りに３１０度の方向に線を引き、１８３５に相当する長さのところに印を入れます｡ ここが部分食開始時刻での月の位置の中心になります。ここを中心に月の大きさにあわせて円を描きます｡ この時、部分食が始まる時刻ですから、月と太陽が接しているはずです。
同様に、７時２９分２８秒(食甚)と８時５３分３２秒(部分食終了)の月の位置､ ２０分ごとの月の中心位置も作図しておきます。食甚時の月の輪郭は太陽を表す太線の内側の境界です｡ 黒く太くなっている部分が、月が太陽に最も入り込んだときの太陽の状態を表しています。
2011.08.13 掲載開始
2011.09.20 加筆
2011.10.30 加筆
2011.12.01 加筆終了
2013.03.03 追記
2020.11.20 配置修正
2011.09.20 加筆
2011.10.30 加筆
2011.12.01 加筆終了
2013.03.03 追記
2020.11.20 配置修正