<均時差とはなにか>
時刻は、太陽が南中すると12時(正午)というように太陽の動きを元に決めていました。この時刻は日時計を使うことで知ることができます。
その後機械式の時計が作られるようになると、2つの時計の時刻がずれるということがわかってきました。
ずれ方は、時期(季節)によって決まった値になります。このずれの大きさを均時差と呼んでいます。
日時計の示す時刻を視太陽時(真太陽時)、時計の示す時刻を平均太陽時といいます。 平均太陽時というのは、天の赤道上を東から西に1年かかって1周する平均太陽を想定し、この平均太陽から求められた時刻という意味になります。 これを使うと均時差は次のように定義されます。
均時差=視太陽時−平均太陽時
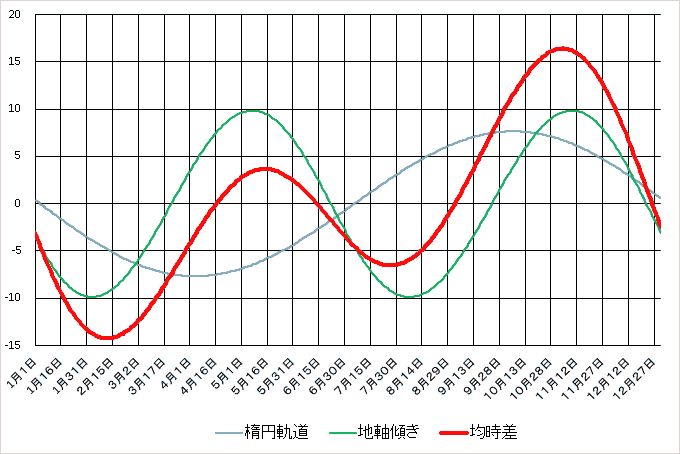
実際に2023年の均時差の大きさを計算してみました。結果をグラフにしたのが次の図です。 赤線で示しています。青線・緑線の意味は後々説明します。縦軸の単位は分になります。 年明けからだんだん小さくなっていって2月12日に−14.2分で最小になった後、5月15日に3.7分と最大になり、 7月27日に−6.5分、11月4日に16.4分と波うつように変化します。
<均時差ができるわけ>
どうして均時差がでるのかを考える前に1日の長さについて考えることにします。
よく勘違いされていることがあります。1日の長さが24時間だから、地球の自転周期も24時間だという勘違いです。 実際には23時間56分4秒です。わずかに短くなっています。この違いが生じる理由を考えてみます。
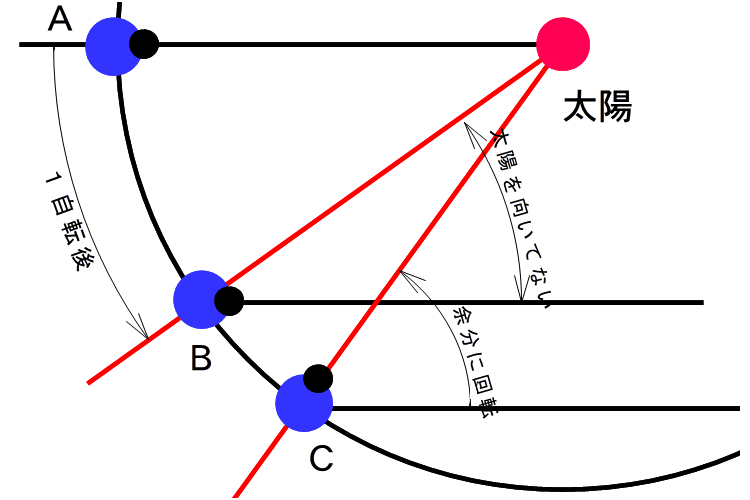 右図で、地球(青丸)がAにいる時に太陽の方向を向いている地点を黒丸で示しています。
ここから、地球が左回りに1回自転した時を考えます。先ほどの地点(黒丸)は地球から見て同じ方向にあります(右なら右)。
地球は1回自転する間に公転によって左回りに少しだけ移動しています。この位置がBになります。
Bでは地球が移動した分太陽が後ろ側に見えます。太陽の方に向くにはもう少しだけ自転する必要があります。
太陽の1日の長さは、余分に自転する分だけ長くなります。
右図で、地球(青丸)がAにいる時に太陽の方向を向いている地点を黒丸で示しています。
ここから、地球が左回りに1回自転した時を考えます。先ほどの地点(黒丸)は地球から見て同じ方向にあります(右なら右)。
地球は1回自転する間に公転によって左回りに少しだけ移動しています。この位置がBになります。
Bでは地球が移動した分太陽が後ろ側に見えます。太陽の方に向くにはもう少しだけ自転する必要があります。
太陽の1日の長さは、余分に自転する分だけ長くなります。
1日の長さと自転周期の関係を計算してみます。1日(24時間)後に地球はCまで移動しています。 Aにいる時に右側にあった星は,この間に1回とちょっとだけ余分に回転しています。太陽はちょうど1回です。 次の1日後はどうでしょう。星も太陽も同じだけ移動してい行きます。 さらに、1日後と続けていけば、星はだんだん右側にずれていきます。
これが1年経つとうなるでしょうか。地球はAの位置まで戻っていますから、最初と同じ位置(太陽と同じ方向)に見えます。 ずれていったのが大きくなり、ちょうど1回まわったことになります。 星は、1年の間に365回と余分に回った1回分をあわせて366回まわることになります。
星が回る周期は1年の長さをそれよりも1だけ大きな数字で割った長さになります。 1年は365.2422日として計算すると
365.2422÷(365.2422+1) = 0.99727 日
= 23.93447 時間 = 23時間56.068分
となります。
星が1回まわる時間、すなわち地球の自転周期を1恒星日といい、太陽の1日を1太陽日といいます。
ところで、均時差があるというのは、1日の長さが日によって違うということを示しています。 地球の自転速度は慣性の法則に従いますから、変化しそうにありません。 長さが変わるとすると、余分にまわる分が関係してきそうです。探ってみます。
余分にまわる大きさが変化する理由は2つあります。1つは地球の公転軌道の形が楕円形ということよるものです。これを「楕円軌道」と呼ぶことにします。 2つ目は、地球の自転軸が公転軸に対して傾いていることです。一般的には地軸が傾向いているといわれていますので「地軸の傾き」とします。 一つずつ詳しく見ていきます。
−−「楕円軌道」について−−
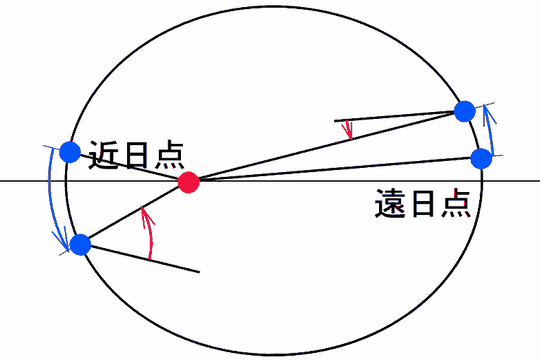 地球を含め惑星の運動はケプラーの法則に従います。
第一法則は楕円軌道の法則とも呼ばれ「惑星の軌道の形は楕円形でその焦点の一つに太陽がある」というものです。
軌道は円形ではないうえに太陽は中心にいないので、地球は太陽に近づいたり、遠ざかったりします。
太陽に一番近づく場所を近日点、遠ざかる場所を遠日点といいます。
地球が同じだけ動いたとしても、近日点近くにいるときは太陽は速く動くように見え、遠日点付近にいるときはゆっくり動くように見えます。
速く動いてみえればその分だけ余分にまわらないといけないので1日の長さが長くなります。
地球を含め惑星の運動はケプラーの法則に従います。
第一法則は楕円軌道の法則とも呼ばれ「惑星の軌道の形は楕円形でその焦点の一つに太陽がある」というものです。
軌道は円形ではないうえに太陽は中心にいないので、地球は太陽に近づいたり、遠ざかったりします。
太陽に一番近づく場所を近日点、遠ざかる場所を遠日点といいます。
地球が同じだけ動いたとしても、近日点近くにいるときは太陽は速く動くように見え、遠日点付近にいるときはゆっくり動くように見えます。
速く動いてみえればその分だけ余分にまわらないといけないので1日の長さが長くなります。
さらに第二法則があります。面積速度一定の法則とも呼ばれ、「動径(惑星と太陽を結ぶ線)が一定時間内に通る場所の面積は一定である」というものです。 面積は動径×速度×時間÷2で計算できます。時間が一定なら動径×速度が一定になります。 これは反比例の関係になりますから、太陽に近いと速く、遠いと遅くなるという関係が導き出せます。 近日点では地球の動きが速くその分太陽の動きも速く見えます。遠日点ではその逆で、太陽の動きもゆっくりになります。
どちらの効果も、近日点で速く、遠日点ではゆっくりになりますから、効果は倍増することになります。
この効果による1日の長さを考えてみます。地球が近日点にいるのは1月の始めで、この頃が1日の長さが最大になります。 7月の始め頃に遠日点にいますから、1日の長さが短い頃になります。
均時差の大きさで考えてみます。均時差は、1日の長さが平均より長かった短かかったかということの積み重ねでできます。 影響がどのようになるかを考えてみます。 1日が長いとその分実際の太陽(以後視太陽とよびます)は遅れていきます。これに伴い視太陽時も遅れていきます。 1月初めと7月はじめのちょうど真ん中の4月始め頃を考えてみます。それまでは1日長さが平均より長かったものが短くなるように変化します。 以後は視太陽時の遅れが取り戻されていきますから、この頃に遅れが最大になります。 同様に10月の始め頃に進みが最大となります。 その真ん中の1月始めと7月初めは均時差が0となります。 このようすは均時差グラフに青線で示しています。
−−「地軸の傾き」について−−
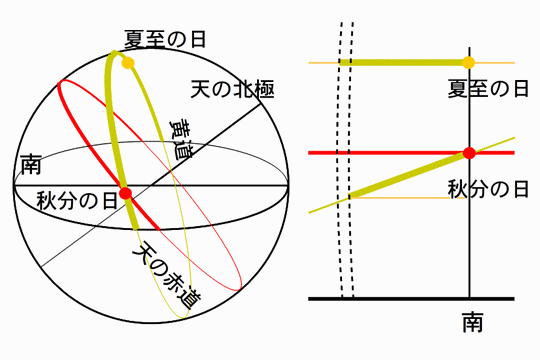 地軸が傾くことによって、公転面(黄道面)に対して地球の赤道面(天の赤道)が傾きます。そのようすを示したのが左側の図です。
黄道を暗黄色線、赤道を赤色線で示しています。見てわかるのは春分秋分の頃は黄道は赤道面に斜めに交わっているのに対して、
夏至・冬至の頃は平行になっています。このことが1太陽日、言いかえると余分にまわる長さにおよぼす影響を考えます。
地軸が傾くことによって、公転面(黄道面)に対して地球の赤道面(天の赤道)が傾きます。そのようすを示したのが左側の図です。
黄道を暗黄色線、赤道を赤色線で示しています。見てわかるのは春分秋分の頃は黄道は赤道面に斜めに交わっているのに対して、
夏至・冬至の頃は平行になっています。このことが1太陽日、言いかえると余分にまわる長さにおよぼす影響を考えます。
夏至・秋分の日に太陽が南中しているようすを考えます。右側の図です。 それぞれの日から1恒星日後の視位置を暗黄色線で結んでいます。地球自転周期を求めた図でB点からの位置になります。 星や太陽は、図中を赤線と平行に左から右に動いていきます。その速度は天の赤道付近(赤線)付近で最も速くそこから離れるに従ってゆっくりになります。
まず秋分の日に注目します。南から垂直にのびるまっすぐな線(天の子午線)からの幅(黄橙線で入れています)は、 1恒星日に動く幅(暗黄色線の長さ)より短くなっています。この頃に1日の長さが最も短くなります。春分の日も同様です。
夏至の日です。天の子午線からのずれ幅は1恒星日に動く幅と全く同じです。ところで、夏至の太陽は天の赤道から離れています。 その分太陽の動き(日周運動による)はゆっくりになりますから、1日の長さは標準(1平均太陽日)より長くなります。 同様に冬至の頃も1日の長さは長くなっています。
楕円軌道の場合の1日の長さと均時差の大きさの関係(最速・最遅の時に0)を応用してみると、均時差の大きさは、 春分・夏至・秋分・冬至で0、間の立夏・立冬で最も進み、立春・立秋で最も遅れます。 このようすは均時差グラフに緑線で示しています。
<均時差を求めてみた>
-−−「楕円軌道」について−−
楕円軌道による均時差を計算するには、軌道上の地球の位置を知る必要があります。 とりあえず、楕円軌道上で近日点通から1日ごとに太陽からみてどの方向に地球があるかを表計算ソフトを使って計算してみます。 データについては天文年鑑2023年版記載のものを用います。また計算方法についても記載されていますからこれを参考に進めていきます。
 考え方です。ここでケプラーの第二法則が必要になります。
動径の通ったところの面積は一定時間なら同じというのは、面積は時間に比例するということでもあります。
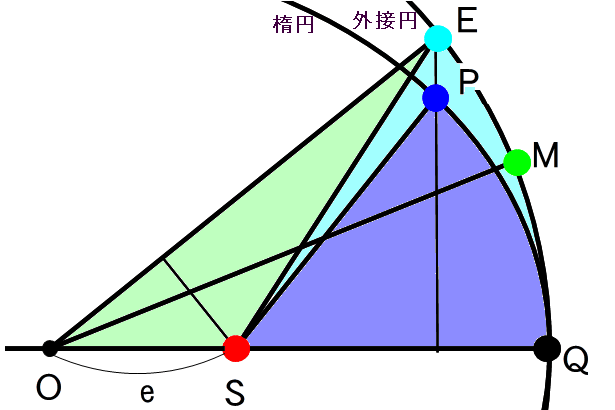
右図で、近日点(Q)を出発した惑星(地球)がT日後にPにいるとします。ケプラーの法則から、扇形QSPの面積(藤色部分)は時間に比例します。
この時の∠QSPが太陽からみたときに惑星が動いた角度になります。Sは太陽の位置です。
求めたいのはこの角度で、真近点角といいます。求めるのは少し複雑になります。
考え方です。ここでケプラーの第二法則が必要になります。
動径の通ったところの面積は一定時間なら同じというのは、面積は時間に比例するということでもあります。
右図で、近日点(Q)を出発した惑星(地球)がT日後にPにいるとします。ケプラーの法則から、扇形QSPの面積(藤色部分)は時間に比例します。
この時の∠QSPが太陽からみたときに惑星が動いた角度になります。Sは太陽の位置です。
求めたいのはこの角度で、真近点角といいます。求めるのは少し複雑になります。
次に、楕円に外接円をかきます。Pから長軸(OQ)方向と反対側に線を伸ばし外接円と交わったところをEとします。 楕円では長軸から直角に引いた線が楕円と交わる点、外接円と交わる点までの距離の比は一定になります。 短軸の長さをbとすると比の値はb/aになりますから、扇形QSEの面積は扇形QSPのb/a倍になり時間に比例することがわかります。 ここで b2=a2(1−e2) の関係があります。eは楕円の離心率で、以後aは1として計算します。
扇形QSEの面積は惑星が1公転すると、外接円の面積と等しくなります。 別に考えなくてもいいのですが、外接円上を同じ公転周期でまわる天体を考えます。同じT日後にいる位置をMとします。 この時に、扇形QSE、扇形QOMは等しくなります。 ∠QOMは一定速度で大きくなっていきます。その速さは平均運動といい、記号はnで表します。 また∠QOMの大きさを平均近点(離)角といいます。記号はMです。さらに、M=nTの関係があります。
次に扇形QSEの面積を求める式を作ります。求める面積は扇形QOE(色で塗った部分全部)の面積から△SOEの面積を引いたものになります。 ここで∠SOEをEとします。この角度を離心近点(離)角といいます。
△SOEで底辺をOEとすれば高さはae×sin(E)になります。よって次の式を作れます。
扇形QSE=扇形QOE − △SOE
a2M/2=a2E/2−a2e×sin(E)/2
M = E − e×sin(E)
この式はケプラー方程式といわれています。普通に解くことはできません。 Eを求めるには、いったん式を E=M+e×sin(E) と変形します。 そのうえで、右辺のEにMを代入して計算し、求められた結果をさらに右辺のEに代入してというのを繰り返し、 計算前と計算後のEの変化量が所定量より少なくなった値をもって計算結果とします。
計算してみます。とりあえず、近日点通過1日後(T=1)の地球の位置(真近点角)を求めることにします。 計算結果は有効数字の桁数に関係なく、表計算ソフトの計算結果をそのまま書きます。 ここで必要なデータは離心率(e)でその値は0.016709です。軌道長半径(a)は1とします。
最初に平均運動を求めます、天文年鑑に計算式が書かれていますから、それにしたがって計算します。
0.9856091×a2/3 = 0.9856091
この結果は、360を恒星年で割ったものになっています。近点年で割った方がよさそうですが、本に従うことにします。 単位は 度/日 です。
次に平均近点角(M)を求めます。 平均運動×日数になります。結果はそのままです。この後は三角関数が入ってきますから、単位をラジアンに変換する必要があります。 57.29577951で割ります。
0.9856091÷57.29577951=0.017202124
M+e×sin(M)に代入します。
0.017202124+0.016709×sin(0.017202124) = 0.016914708
この結果をM+e×sin(M)のMに代入して計算前の値と比較していきます。これを何回か繰り返します。
回 結果 差
1回目 0.017484738 0.00057003
2回目 0.017494262 9.52323E-06
3回目 0.017494421 1.59099E-07
4回目 0.017494423 2.65798E-09
5回目 0.017494423 4.44055E-11
6回目 0.017494423 7.41858E-13
7回目 0.017494423 1.23929E-14
3回目くらいでだいたい必要な精度が出ているようです。 表計算ソフトでは、ゴールシークを使えば結果をだしてくれるようですが、日毎に目標値を入れるのは面倒です。 多めに繰り返しておけは時間がかかる以外は特段問題はありません。7回(Mを代入したのを入れると8回)程度繰り返したものを結果とします。
 真近点離角を求めます。天文年鑑には、太陽を原点とする直交座標上で地球の座標を求める式が書かれています。
これを応用します。次の式です(一部変形しています)。
真近点離角を求めます。天文年鑑には、太陽を原点とする直交座標上で地球の座標を求める式が書かれています。
これを応用します。次の式です(一部変形しています)。
x=r×cos(ν)=cos(E)−e
y=r×sin(ν)=b×sin(E)
ここで、rは動径、bは短半径です。
xはふつうに三角比から、yはPのy座標がEのもののb倍になるという関係から求められています。
rがわからないので式を作ります。xyを求める式をそれぞれ2乗して加えてみます。
x2+y2 =
r2cos2(ν)+r2sin2(ν)=r2
=[cos(E)-e]2+b2×sin2(E)
=cos2(E)-2e cos(E)+e2+(1-e2)sin2(E)
=cos2(E)+sin2(E)-2e cos(E)+e2 - e2sin2(E)
=1-2e cos(E)+e2cos2(E)
=[1-e cos(E)]2
2番目の式と最後の式から
r=1−ecos(E)
が求められます。x座標を求める式を変形してえられる次の式を使って真近点角を求めることにします。
cos(ν)=[cos(E)−e]÷[1−ecos(E)]
計算結果は
0.017789206 rad , 1.019246408度
となります。
必要なデータそろいましたので、軌道形が楕円である事の影響(時差)を求めます。 均時差は視太陽時から平均太陽時を引いたものになります。 従って実際の太陽が示す時刻と、天の赤道上を一定速度で動く太陽が示す時刻との差を時差とします。 ところで、ここまででは太陽から地球の見える方角は計算ました。地球から太陽の見える方角は計算していません。 実際には、「太陽から」の方角と「地球から」の方角は正反対になりますから、一方から他方を求めるには180度を加えれ(または引け)ばよいことになります。 時差を求めるには2つの地球からの方角の差を求めます。太陽からの方角の差にどちらも180度を加えてから差を取ることになります。 180度の部分は、差をとったときに消されてしまいますから、単純に太陽からの方角の差を求めても同じ結果が得られます。 いちいち地球からの方角に変換せずにそのまま計算することにします。
平均近点離角は軌道上を一定速度で動いていますから、平均太陽(の正反対側)と見なせます。真近点角が視太陽(正反対側)として計算します。 太陽時は、南中した時を12時(正午)として、そこからの経過時間を加えて求めます。 南中してからの経過時間を時角といいます。単位は時間を使います。ここでは計算の都合上度で考えることにします。1時間は15度になります。 時角をつかうと次の式が作れます。
太陽時 = 太陽の時角 + 12時
星の経度は春分点が南中してから、その天体が南中するまでの時間で表します。そのために次の式が成り立ちます。
天体の南中時刻 = 春分点の南中時刻 + 天体の経度
天体を太陽に置き換えて式を整理すると
春分点の南中時刻 = 12時 − 太陽の経度
となります。
春分点の南中時刻を、視太陽時で求めるときは太陽経度は真近点角です。平均太陽時で求めるときは平均近点角なので
(均)時差 = 視太陽時 - 平均太陽時
= 12-視太陽の経度-(12-平均太陽の経度)
= 12−真近点角-(12−平均近点角)
= 平均近点角 − 真近点角
となります。近日点通過翌日では計算した数値を代入して
0.9856091−1.019246408=-0.033637308度
=-0.134549232分
が求められます。
楕円軌道のみを考える場合、近日点通過時は時差が0になります。 この時に視太陽と同じところに平均太陽がありますから、ここでの結果はそのまま時差として扱うことができます。
途中の計算に三角関数とその逆関数が使われています。象限の違いによって式が変わってきます。 表計算ソフトでは自動計算とかを考えないのなら、条件式を使うよりは、結果を見て式を使い分けた方が簡単です。計算は一部この方法でおこなっています。
−−均時差を求める−−
順番としては、地軸の傾きによって生じる時差を求めることになります。 問題があります。春分・夏至・秋分・冬至の間隔は等しくありません。その中間点でもそうです。 とりあえず太陽の実際の運行にあわせて、計算することにします。 方法としては太陽と同じ角度だけ進んだ平均太陽を考え。そこから時差をを求めることにします。 なお、楕円軌道の時差では単に経度で求めました。今回は地球の自転にともなう経度が問題になってきます。 時差は地球の自転に基づいた赤道座標系での経度(赤経)差で求めることになります。
この計算をするためにには、、地球は軌道上の定めた時刻にどこにいるかという情報が必要です。決まった場所にいる時刻でもかまいません。 天文年鑑のデータからは、その手がかりとなるものがありません。 普通に使われるのは、近日点通過の日時時刻か、元期と呼ばれる特定日時時刻の近日点からの位置関係が使われます。
それらしいデータが見当たらないので、毎月の空に書かれている近日点通過日を代入してみました。 2023年版では1月5日1時17分です。計算結果は二十四節気全ての日において1日ずれます。 原因は、記載されている近日点通過は地球が最も太陽に近づく日を示しているからだとわかりました。 地球は月といっしょに太陽を回っています。月と地球は共通重心を中心にして回転してます。 この回転で地球が太陽に近づいたり遠ざかったりする影響で、近日点通過が共通重心が通過する日とずれるようです。
1日ずらして計算してもいい、言い換えれば例えば春分点通過日にあわせて軌道位置を求めることもできます。 これだと、地球は求められても、他の惑星では求めることができません。この方法はは保留としておきます。
天文年鑑の軌道要素欄には平均黄経というのが書かれています。 詳しく書かれているところをみつけていないのですが、その年の1月1日0時(日本標準時で9時)を元期としたときの平均近点角、 2020版以前は春分点からの平均離角のようです。これを使って1月2日(9時JST)を例に計算してみます。
1月1日の平均近点角が357.062(−2.938)度ですから、1月2日の平均近点離角は
-2.938+0.9856091×1=-1.9523909
後は真近点離角まで前回と同じように計算して、
-0.03523842(rad) -2.0190127361度
が求められます。これに近日点黄経を加えることで地球の黄経が求められます。近日点黄経は103.0126度です。
-2.0190127361+103.0126=100.9935873
地球の黄経が求められたところで、その位置が正しいのかの検証をしてみます。
天文年鑑には二十四節気の日時刻が記載されています。 1年間の地球黄経を求めて比較します。二十四節気は地球黄経(太陽黄経)が15度の倍数になる日毎に順番に名前をついています。 その数値を超えない最後の日を、二十四節気とします。比べてみるとたいたい一致します。ただし、小寒のみが1日早くなっています。 小寒になるのが1月6日の0時3分とわずかの差で6日にまわっています。各節気でも時間単位でみるとずれがあるようです。 全体的にわずかな誤差が含まれているようです。原因は不明です。とりあえずこのまま進めます。
一般的には南中時刻を求めるには、赤道座標系(赤経・赤緯)に変換する必要がありまます。その前に。地球公転面からいったん黄道座標系に変換します。 といってもその差は0.0030度とわずかなので、無視して進めます。地球黄経がそのまま黄経に、黄緯は0度となります。 地軸の傾きは黄道傾(斜)角(ε)といいその大きさは23度26分10.399秒角です。 黄緯0の場合黄経(L)から赤道座標系(α,δ)への変換は、黄道傾角を使って
cos(α)・cos(δ)=cos(L) , sin(δ)=sin(L)×sin(ε)
の関係があります。計算すると
sin(δ) = sin(100.9935873)・sin(23.43620528)
= 0.390428854
δ = 22.98118659 度
cos(α) = cos(100.9935873)/cos(22.98118659)
α = 101.9547496 度
が求められます。ふつう赤経の単位は時間ですが、説明の都合上、度にしています。
ここまで計算してしまうと、均時差がすぐに求められます。 これには楕円軌道での(均)時差を求めたときと同じ式が使えます。ただし、経度は全て赤経で統一しないといけません。 平均太陽の位置がはっきりしませんから、近日点(と同じ赤経の位置)を実際の地球と同時にスタートする仮平均地球を想定します。 近日点からの一定速度で進む仮想天体の位置は平均離角で求めています。この仮想天体が仮平均地球になります。 仮平均地球の赤経は、平均離角に近日点の位置(近日点黄経)加えたものになります。 仮平均地球赤経=(-1.9523909)+103.0126
=101.0602091
実際の太陽の赤経を引けば仮の均時差になります。
101.0602091-101.9547496=-0.894540512度
=-3.578162048分
仮平均地球の初期位置を適当に決めています。計算結果を1年間で平均すると、平均地球とのずれだけが残ります。 平均値はは0.001063504分となりますからこれを引いた
-3.578162048-0.001063504=-3.579225552分
が均時差となります。
◎均時差が求まってしまったので、計算する必要がなくなりましたが、どの程度の影響があるのかという意味で地軸のずれによる時差も計算してます。 春分・夏至・秋分・冬至の間隔が等しくない事への対応法が問題となってきます。対応方法は2通りあります。 一つは、実際の太陽の動きに合わせて、何月何日はこれくらいと求める方法です。太陽の位置を求めるのはなかなかの難題です。 ところが、ここまでに計算済なので、それを利用できます。
これに対してもう一つの方法は、太陽の位置がここなら時差はこれくらいと求める方法です。 春分の日の均時差は、雨水ならというように考えていきます。最初からの計算はこちらの方があるかに簡単です。 前者の場合をケプラー運動している場合、後者の場合を等速運動をしている場合として求めてみます。
○ケプラー運動の場合
太陽の赤経からそのまま黄経を引くことで求められます。 計算結果を使うなら、地球の黄経を仮平均地球の赤経とし、時差を求める式に代入します。
100.9935873-101.9547496=-0.961162348度
=-3.844649392分
均時差を求めたときと同様、仮平均地球は初期値を適当に決めていますから、平均値が0になるように調整します。 12月31日まで求めて平均をとると-0.001404366分ですからこれを引いて
3.844649392-(-0.001404366)=3.846053758分
が求められます。
○等速運動の場合
春分点を視太陽と同時に通過する仮平均太陽を考えます。これに180度を加えたものが(太陽からみた)視地球、仮平均地球になります。 1日に動く大きさ(平均運動)は一定です。1太陽年で黄道を一周しますから、1日の平均運動は太陽年で割った値を使うことにします。
360度÷365.24219日=0.985647362度/日
春分の日は、1月1日から数えて79日目です。1月2日は春分の78日前になりますから、地球の黄経は
180-78×0.985647362=103.1195058
これが地球の黄経になりますし、仮平均地球の赤経になります。
地球の位置を赤経と赤緯に変換します。
赤経=104.2529327度 、赤緯=1.133426974度
が求められます。これから仮時差は、
103.1195058−104.2529327=-1.133426974度
=-4.533707895分
他の時差・均時差と同様平均値を求めてその値を引くことで
時差=-4.536374241分
が求められます。
最後にグラフを書かせます。たくさんの列を途中の計算に使っています。必要な列だけを別のシートに貼りつけてそこからグラフを書かせる方が簡単でしょう。 なお、欽一展通過時からではなく、元期(1月1日0時))からの計算をしています。 またグラフは、楕円軌道時差では元期からの計算結果を用いています。地軸傾きによる時差についても日にち(ケプラー運動の場合)にあわせています。 最初に載せたグラフはこの方法で書かせたものです。
ここまでの計算をした内容をxls形式のファイルにしています。
ここからダウンロードできます。zip形式に圧縮しています。
読みこみファイル名wisp18-08.zip サイズ253,952 バイト
解凍ファイル名 wisp18-08.xls サイズ627,200 バイト
 |
|
兵庫県西脇市経緯度交差点(北緯35度東経135度)前にある日時計
後方にあるは経緯度交差点(大正10年測量)の標石などです
|
日時計の示す時刻を視太陽時(真太陽時)、時計の示す時刻を平均太陽時といいます。 平均太陽時というのは、天の赤道上を東から西に1年かかって1周する平均太陽を想定し、この平均太陽から求められた時刻という意味になります。 これを使うと均時差は次のように定義されます。
均時差=視太陽時−平均太陽時
書物(wikipediaも)等によっては逆順になっていることもあります。(by 国立天文台)
実際に2023年の均時差の大きさを計算してみました。結果をグラフにしたのが次の図です。 赤線で示しています。青線・緑線の意味は後々説明します。縦軸の単位は分になります。 年明けからだんだん小さくなっていって2月12日に−14.2分で最小になった後、5月15日に3.7分と最大になり、 7月27日に−6.5分、11月4日に16.4分と波うつように変化します。
<均時差ができるわけ>
どうして均時差がでるのかを考える前に1日の長さについて考えることにします。
よく勘違いされていることがあります。1日の長さが24時間だから、地球の自転周期も24時間だという勘違いです。 実際には23時間56分4秒です。わずかに短くなっています。この違いが生じる理由を考えてみます。
 右図で、地球(青丸)がAにいる時に太陽の方向を向いている地点を黒丸で示しています。
ここから、地球が左回りに1回自転した時を考えます。先ほどの地点(黒丸)は地球から見て同じ方向にあります(右なら右)。
地球は1回自転する間に公転によって左回りに少しだけ移動しています。この位置がBになります。
Bでは地球が移動した分太陽が後ろ側に見えます。太陽の方に向くにはもう少しだけ自転する必要があります。
太陽の1日の長さは、余分に自転する分だけ長くなります。
右図で、地球(青丸)がAにいる時に太陽の方向を向いている地点を黒丸で示しています。
ここから、地球が左回りに1回自転した時を考えます。先ほどの地点(黒丸)は地球から見て同じ方向にあります(右なら右)。
地球は1回自転する間に公転によって左回りに少しだけ移動しています。この位置がBになります。
Bでは地球が移動した分太陽が後ろ側に見えます。太陽の方に向くにはもう少しだけ自転する必要があります。
太陽の1日の長さは、余分に自転する分だけ長くなります。1日の長さと自転周期の関係を計算してみます。1日(24時間)後に地球はCまで移動しています。 Aにいる時に右側にあった星は,この間に1回とちょっとだけ余分に回転しています。太陽はちょうど1回です。 次の1日後はどうでしょう。星も太陽も同じだけ移動してい行きます。 さらに、1日後と続けていけば、星はだんだん右側にずれていきます。
これが1年経つとうなるでしょうか。地球はAの位置まで戻っていますから、最初と同じ位置(太陽と同じ方向)に見えます。 ずれていったのが大きくなり、ちょうど1回まわったことになります。 星は、1年の間に365回と余分に回った1回分をあわせて366回まわることになります。
星が回る周期は1年の長さをそれよりも1だけ大きな数字で割った長さになります。 1年は365.2422日として計算すると
365.2422÷(365.2422+1) = 0.99727 日
= 23.93447 時間 = 23時間56.068分
となります。
星が1回まわる時間、すなわち地球の自転周期を1恒星日といい、太陽の1日を1太陽日といいます。
−−−−−−−−−−
ところで、均時差があるというのは、1日の長さが日によって違うということを示しています。 地球の自転速度は慣性の法則に従いますから、変化しそうにありません。 長さが変わるとすると、余分にまわる分が関係してきそうです。探ってみます。
余分にまわる大きさが変化する理由は2つあります。1つは地球の公転軌道の形が楕円形ということよるものです。これを「楕円軌道」と呼ぶことにします。 2つ目は、地球の自転軸が公転軸に対して傾いていることです。一般的には地軸が傾向いているといわれていますので「地軸の傾き」とします。 一つずつ詳しく見ていきます。
−−「楕円軌道」について−−
 地球を含め惑星の運動はケプラーの法則に従います。
第一法則は楕円軌道の法則とも呼ばれ「惑星の軌道の形は楕円形でその焦点の一つに太陽がある」というものです。
軌道は円形ではないうえに太陽は中心にいないので、地球は太陽に近づいたり、遠ざかったりします。
太陽に一番近づく場所を近日点、遠ざかる場所を遠日点といいます。
地球が同じだけ動いたとしても、近日点近くにいるときは太陽は速く動くように見え、遠日点付近にいるときはゆっくり動くように見えます。
速く動いてみえればその分だけ余分にまわらないといけないので1日の長さが長くなります。
地球を含め惑星の運動はケプラーの法則に従います。
第一法則は楕円軌道の法則とも呼ばれ「惑星の軌道の形は楕円形でその焦点の一つに太陽がある」というものです。
軌道は円形ではないうえに太陽は中心にいないので、地球は太陽に近づいたり、遠ざかったりします。
太陽に一番近づく場所を近日点、遠ざかる場所を遠日点といいます。
地球が同じだけ動いたとしても、近日点近くにいるときは太陽は速く動くように見え、遠日点付近にいるときはゆっくり動くように見えます。
速く動いてみえればその分だけ余分にまわらないといけないので1日の長さが長くなります。さらに第二法則があります。面積速度一定の法則とも呼ばれ、「動径(惑星と太陽を結ぶ線)が一定時間内に通る場所の面積は一定である」というものです。 面積は動径×速度×時間÷2で計算できます。時間が一定なら動径×速度が一定になります。 これは反比例の関係になりますから、太陽に近いと速く、遠いと遅くなるという関係が導き出せます。 近日点では地球の動きが速くその分太陽の動きも速く見えます。遠日点ではその逆で、太陽の動きもゆっくりになります。
どちらの効果も、近日点で速く、遠日点ではゆっくりになりますから、効果は倍増することになります。
この効果による1日の長さを考えてみます。地球が近日点にいるのは1月の始めで、この頃が1日の長さが最大になります。 7月の始め頃に遠日点にいますから、1日の長さが短い頃になります。
均時差の大きさで考えてみます。均時差は、1日の長さが平均より長かった短かかったかということの積み重ねでできます。 影響がどのようになるかを考えてみます。 1日が長いとその分実際の太陽(以後視太陽とよびます)は遅れていきます。これに伴い視太陽時も遅れていきます。 1月初めと7月はじめのちょうど真ん中の4月始め頃を考えてみます。それまでは1日長さが平均より長かったものが短くなるように変化します。 以後は視太陽時の遅れが取り戻されていきますから、この頃に遅れが最大になります。 同様に10月の始め頃に進みが最大となります。 その真ん中の1月始めと7月初めは均時差が0となります。 このようすは均時差グラフに青線で示しています。
−−「地軸の傾き」について−−
 地軸が傾くことによって、公転面(黄道面)に対して地球の赤道面(天の赤道)が傾きます。そのようすを示したのが左側の図です。
黄道を暗黄色線、赤道を赤色線で示しています。見てわかるのは春分秋分の頃は黄道は赤道面に斜めに交わっているのに対して、
夏至・冬至の頃は平行になっています。このことが1太陽日、言いかえると余分にまわる長さにおよぼす影響を考えます。
地軸が傾くことによって、公転面(黄道面)に対して地球の赤道面(天の赤道)が傾きます。そのようすを示したのが左側の図です。
黄道を暗黄色線、赤道を赤色線で示しています。見てわかるのは春分秋分の頃は黄道は赤道面に斜めに交わっているのに対して、
夏至・冬至の頃は平行になっています。このことが1太陽日、言いかえると余分にまわる長さにおよぼす影響を考えます。夏至・秋分の日に太陽が南中しているようすを考えます。右側の図です。 それぞれの日から1恒星日後の視位置を暗黄色線で結んでいます。地球自転周期を求めた図でB点からの位置になります。 星や太陽は、図中を赤線と平行に左から右に動いていきます。その速度は天の赤道付近(赤線)付近で最も速くそこから離れるに従ってゆっくりになります。
まず秋分の日に注目します。南から垂直にのびるまっすぐな線(天の子午線)からの幅(黄橙線で入れています)は、 1恒星日に動く幅(暗黄色線の長さ)より短くなっています。この頃に1日の長さが最も短くなります。春分の日も同様です。
夏至の日です。天の子午線からのずれ幅は1恒星日に動く幅と全く同じです。ところで、夏至の太陽は天の赤道から離れています。 その分太陽の動き(日周運動による)はゆっくりになりますから、1日の長さは標準(1平均太陽日)より長くなります。 同様に冬至の頃も1日の長さは長くなっています。
楕円軌道の場合の1日の長さと均時差の大きさの関係(最速・最遅の時に0)を応用してみると、均時差の大きさは、 春分・夏至・秋分・冬至で0、間の立夏・立冬で最も進み、立春・立秋で最も遅れます。 このようすは均時差グラフに緑線で示しています。
<均時差を求めてみた>
-−−「楕円軌道」について−−
楕円軌道による均時差を計算するには、軌道上の地球の位置を知る必要があります。 とりあえず、楕円軌道上で近日点通から1日ごとに太陽からみてどの方向に地球があるかを表計算ソフトを使って計算してみます。 データについては天文年鑑2023年版記載のものを用います。また計算方法についても記載されていますからこれを参考に進めていきます。
 考え方です。ここでケプラーの第二法則が必要になります。
動径の通ったところの面積は一定時間なら同じというのは、面積は時間に比例するということでもあります。
右図で、近日点(Q)を出発した惑星(地球)がT日後にPにいるとします。ケプラーの法則から、扇形QSPの面積(藤色部分)は時間に比例します。
この時の∠QSPが太陽からみたときに惑星が動いた角度になります。Sは太陽の位置です。
求めたいのはこの角度で、真近点角といいます。求めるのは少し複雑になります。
考え方です。ここでケプラーの第二法則が必要になります。
動径の通ったところの面積は一定時間なら同じというのは、面積は時間に比例するということでもあります。
右図で、近日点(Q)を出発した惑星(地球)がT日後にPにいるとします。ケプラーの法則から、扇形QSPの面積(藤色部分)は時間に比例します。
この時の∠QSPが太陽からみたときに惑星が動いた角度になります。Sは太陽の位置です。
求めたいのはこの角度で、真近点角といいます。求めるのは少し複雑になります。次に、楕円に外接円をかきます。Pから長軸(OQ)方向と反対側に線を伸ばし外接円と交わったところをEとします。 楕円では長軸から直角に引いた線が楕円と交わる点、外接円と交わる点までの距離の比は一定になります。 短軸の長さをbとすると比の値はb/aになりますから、扇形QSEの面積は扇形QSPのb/a倍になり時間に比例することがわかります。 ここで b2=a2(1−e2) の関係があります。eは楕円の離心率で、以後aは1として計算します。
扇形QSEの面積は惑星が1公転すると、外接円の面積と等しくなります。 別に考えなくてもいいのですが、外接円上を同じ公転周期でまわる天体を考えます。同じT日後にいる位置をMとします。 この時に、扇形QSE、扇形QOMは等しくなります。 ∠QOMは一定速度で大きくなっていきます。その速さは平均運動といい、記号はnで表します。 また∠QOMの大きさを平均近点(離)角といいます。記号はMです。さらに、M=nTの関係があります。
次に扇形QSEの面積を求める式を作ります。求める面積は扇形QOE(色で塗った部分全部)の面積から△SOEの面積を引いたものになります。 ここで∠SOEをEとします。この角度を離心近点(離)角といいます。
△SOEで底辺をOEとすれば高さはae×sin(E)になります。よって次の式を作れます。
扇形QSE=扇形QOE − △SOE
a2M/2=a2E/2−a2e×sin(E)/2
M = E − e×sin(E)
この式はケプラー方程式といわれています。普通に解くことはできません。 Eを求めるには、いったん式を E=M+e×sin(E) と変形します。 そのうえで、右辺のEにMを代入して計算し、求められた結果をさらに右辺のEに代入してというのを繰り返し、 計算前と計算後のEの変化量が所定量より少なくなった値をもって計算結果とします。
計算してみます。とりあえず、近日点通過1日後(T=1)の地球の位置(真近点角)を求めることにします。 計算結果は有効数字の桁数に関係なく、表計算ソフトの計算結果をそのまま書きます。 ここで必要なデータは離心率(e)でその値は0.016709です。軌道長半径(a)は1とします。
最初に平均運動を求めます、天文年鑑に計算式が書かれていますから、それにしたがって計算します。
0.9856091×a2/3 = 0.9856091
この結果は、360を恒星年で割ったものになっています。近点年で割った方がよさそうですが、本に従うことにします。 単位は 度/日 です。
次に平均近点角(M)を求めます。 平均運動×日数になります。結果はそのままです。この後は三角関数が入ってきますから、単位をラジアンに変換する必要があります。 57.29577951で割ります。
0.9856091÷57.29577951=0.017202124
M+e×sin(M)に代入します。
0.017202124+0.016709×sin(0.017202124) = 0.016914708
この結果をM+e×sin(M)のMに代入して計算前の値と比較していきます。これを何回か繰り返します。
回 結果 差
1回目 0.017484738 0.00057003
2回目 0.017494262 9.52323E-06
3回目 0.017494421 1.59099E-07
4回目 0.017494423 2.65798E-09
5回目 0.017494423 4.44055E-11
6回目 0.017494423 7.41858E-13
7回目 0.017494423 1.23929E-14
3回目くらいでだいたい必要な精度が出ているようです。 表計算ソフトでは、ゴールシークを使えば結果をだしてくれるようですが、日毎に目標値を入れるのは面倒です。 多めに繰り返しておけは時間がかかる以外は特段問題はありません。7回(Mを代入したのを入れると8回)程度繰り返したものを結果とします。
 真近点離角を求めます。天文年鑑には、太陽を原点とする直交座標上で地球の座標を求める式が書かれています。
これを応用します。次の式です(一部変形しています)。
真近点離角を求めます。天文年鑑には、太陽を原点とする直交座標上で地球の座標を求める式が書かれています。
これを応用します。次の式です(一部変形しています)。x=r×cos(ν)=cos(E)−e
y=r×sin(ν)=b×sin(E)
ここで、rは動径、bは短半径です。
xはふつうに三角比から、yはPのy座標がEのもののb倍になるという関係から求められています。
rがわからないので式を作ります。xyを求める式をそれぞれ2乗して加えてみます。
x2+y2 =
r2cos2(ν)+r2sin2(ν)=r2
=[cos(E)-e]2+b2×sin2(E)
=cos2(E)-2e cos(E)+e2+(1-e2)sin2(E)
=cos2(E)+sin2(E)-2e cos(E)+e2
=1-2e cos(E)+e2cos2(E)
=[1-e cos(E)]2
2番目の式と最後の式から
r=1−ecos(E)
が求められます。x座標を求める式を変形してえられる次の式を使って真近点角を求めることにします。
cos(ν)=[cos(E)−e]÷[1−ecos(E)]
| ※ | tan(ν/2)=[(1+e)/(1-e)]1/2tan(E/2) の関係があります。計算時にわかっていなかったので使っていません。 式の導き出し方をみるには右をクリック。 →式をみる/閉じる |
計算結果は
0.017789206 rad , 1.019246408度
となります。
必要なデータそろいましたので、軌道形が楕円である事の影響(時差)を求めます。 均時差は視太陽時から平均太陽時を引いたものになります。 従って実際の太陽が示す時刻と、天の赤道上を一定速度で動く太陽が示す時刻との差を時差とします。 ところで、ここまででは太陽から地球の見える方角は計算ました。地球から太陽の見える方角は計算していません。 実際には、「太陽から」の方角と「地球から」の方角は正反対になりますから、一方から他方を求めるには180度を加えれ(または引け)ばよいことになります。 時差を求めるには2つの地球からの方角の差を求めます。太陽からの方角の差にどちらも180度を加えてから差を取ることになります。 180度の部分は、差をとったときに消されてしまいますから、単純に太陽からの方角の差を求めても同じ結果が得られます。 いちいち地球からの方角に変換せずにそのまま計算することにします。
平均近点離角は軌道上を一定速度で動いていますから、平均太陽(の正反対側)と見なせます。真近点角が視太陽(正反対側)として計算します。 太陽時は、南中した時を12時(正午)として、そこからの経過時間を加えて求めます。 南中してからの経過時間を時角といいます。単位は時間を使います。ここでは計算の都合上度で考えることにします。1時間は15度になります。 時角をつかうと次の式が作れます。
太陽時 = 太陽の時角 + 12時
星の経度は春分点が南中してから、その天体が南中するまでの時間で表します。そのために次の式が成り立ちます。
天体の南中時刻 = 春分点の南中時刻 + 天体の経度
天体を太陽に置き換えて式を整理すると
春分点の南中時刻 = 12時 − 太陽の経度
となります。
春分点の南中時刻を、視太陽時で求めるときは太陽経度は真近点角です。平均太陽時で求めるときは平均近点角なので
(均)時差 = 視太陽時 - 平均太陽時
= 12-視太陽の経度-(12-平均太陽の経度)
= 12−真近点角-(12−平均近点角)
= 平均近点角 − 真近点角
となります。近日点通過翌日では計算した数値を代入して
0.9856091−1.019246408=-0.033637308度
=-0.134549232分
が求められます。
楕円軌道のみを考える場合、近日点通過時は時差が0になります。 この時に視太陽と同じところに平均太陽がありますから、ここでの結果はそのまま時差として扱うことができます。
途中の計算に三角関数とその逆関数が使われています。象限の違いによって式が変わってきます。 表計算ソフトでは自動計算とかを考えないのなら、条件式を使うよりは、結果を見て式を使い分けた方が簡単です。計算は一部この方法でおこなっています。
−−均時差を求める−−
順番としては、地軸の傾きによって生じる時差を求めることになります。 問題があります。春分・夏至・秋分・冬至の間隔は等しくありません。その中間点でもそうです。 とりあえず太陽の実際の運行にあわせて、計算することにします。 方法としては太陽と同じ角度だけ進んだ平均太陽を考え。そこから時差をを求めることにします。 なお、楕円軌道の時差では単に経度で求めました。今回は地球の自転にともなう経度が問題になってきます。 時差は地球の自転に基づいた赤道座標系での経度(赤経)差で求めることになります。
この計算をするためにには、、地球は軌道上の定めた時刻にどこにいるかという情報が必要です。決まった場所にいる時刻でもかまいません。 天文年鑑のデータからは、その手がかりとなるものがありません。 普通に使われるのは、近日点通過の日時時刻か、元期と呼ばれる特定日時時刻の近日点からの位置関係が使われます。
それらしいデータが見当たらないので、毎月の空に書かれている近日点通過日を代入してみました。 2023年版では1月5日1時17分です。計算結果は二十四節気全ての日において1日ずれます。 原因は、記載されている近日点通過は地球が最も太陽に近づく日を示しているからだとわかりました。 地球は月といっしょに太陽を回っています。月と地球は共通重心を中心にして回転してます。 この回転で地球が太陽に近づいたり遠ざかったりする影響で、近日点通過が共通重心が通過する日とずれるようです。
1日ずらして計算してもいい、言い換えれば例えば春分点通過日にあわせて軌道位置を求めることもできます。 これだと、地球は求められても、他の惑星では求めることができません。この方法はは保留としておきます。
天文年鑑の軌道要素欄には平均黄経というのが書かれています。 詳しく書かれているところをみつけていないのですが、その年の1月1日0時(日本標準時で9時)を元期としたときの平均近点角、 2020版以前は春分点からの平均離角のようです。これを使って1月2日(9時JST)を例に計算してみます。
1月1日の平均近点角が357.062(−2.938)度ですから、1月2日の平均近点離角は
-2.938+0.9856091×1=-1.9523909
後は真近点離角まで前回と同じように計算して、
-0.03523842(rad) -2.0190127361度
が求められます。これに近日点黄経を加えることで地球の黄経が求められます。近日点黄経は103.0126度です。
-2.0190127361+103.0126=100.9935873
地球の黄経が求められたところで、その位置が正しいのかの検証をしてみます。
天文年鑑には二十四節気の日時刻が記載されています。 1年間の地球黄経を求めて比較します。二十四節気は地球黄経(太陽黄経)が15度の倍数になる日毎に順番に名前をついています。 その数値を超えない最後の日を、二十四節気とします。比べてみるとたいたい一致します。ただし、小寒のみが1日早くなっています。 小寒になるのが1月6日の0時3分とわずかの差で6日にまわっています。各節気でも時間単位でみるとずれがあるようです。 全体的にわずかな誤差が含まれているようです。原因は不明です。とりあえずこのまま進めます。
一般的には南中時刻を求めるには、赤道座標系(赤経・赤緯)に変換する必要がありまます。その前に。地球公転面からいったん黄道座標系に変換します。 といってもその差は0.0030度とわずかなので、無視して進めます。地球黄経がそのまま黄経に、黄緯は0度となります。 地軸の傾きは黄道傾(斜)角(ε)といいその大きさは23度26分10.399秒角です。 黄緯0の場合黄経(L)から赤道座標系(α,δ)への変換は、黄道傾角を使って
cos(α)・cos(δ)=cos(L) , sin(δ)=sin(L)×sin(ε)
の関係があります。計算すると
sin(δ) = sin(100.9935873)・sin(23.43620528)
= 0.390428854
δ = 22.98118659 度
cos(α) = cos(100.9935873)/cos(22.98118659)
α = 101.9547496 度
が求められます。ふつう赤経の単位は時間ですが、説明の都合上、度にしています。
ここまで計算してしまうと、均時差がすぐに求められます。 これには楕円軌道での(均)時差を求めたときと同じ式が使えます。ただし、経度は全て赤経で統一しないといけません。 平均太陽の位置がはっきりしませんから、近日点(と同じ赤経の位置)を実際の地球と同時にスタートする仮平均地球を想定します。 近日点からの一定速度で進む仮想天体の位置は平均離角で求めています。この仮想天体が仮平均地球になります。 仮平均地球の赤経は、平均離角に近日点の位置(近日点黄経)加えたものになります。 仮平均地球赤経=(-1.9523909)+103.0126
=101.0602091
実際の太陽の赤経を引けば仮の均時差になります。
101.0602091-101.9547496=-0.894540512度
=-3.578162048分
仮平均地球の初期位置を適当に決めています。計算結果を1年間で平均すると、平均地球とのずれだけが残ります。 平均値はは0.001063504分となりますからこれを引いた
-3.578162048-0.001063504=-3.579225552分
が均時差となります。
◎均時差が求まってしまったので、計算する必要がなくなりましたが、どの程度の影響があるのかという意味で地軸のずれによる時差も計算してます。 春分・夏至・秋分・冬至の間隔が等しくない事への対応法が問題となってきます。対応方法は2通りあります。 一つは、実際の太陽の動きに合わせて、何月何日はこれくらいと求める方法です。太陽の位置を求めるのはなかなかの難題です。 ところが、ここまでに計算済なので、それを利用できます。
これに対してもう一つの方法は、太陽の位置がここなら時差はこれくらいと求める方法です。 春分の日の均時差は、雨水ならというように考えていきます。最初からの計算はこちらの方があるかに簡単です。 前者の場合をケプラー運動している場合、後者の場合を等速運動をしている場合として求めてみます。
○ケプラー運動の場合
太陽の赤経からそのまま黄経を引くことで求められます。 計算結果を使うなら、地球の黄経を仮平均地球の赤経とし、時差を求める式に代入します。
100.9935873-101.9547496=-0.961162348度
=-3.844649392分
均時差を求めたときと同様、仮平均地球は初期値を適当に決めていますから、平均値が0になるように調整します。 12月31日まで求めて平均をとると-0.001404366分ですからこれを引いて
3.844649392-(-0.001404366)=3.846053758分
が求められます。
○等速運動の場合
春分点を視太陽と同時に通過する仮平均太陽を考えます。これに180度を加えたものが(太陽からみた)視地球、仮平均地球になります。 1日に動く大きさ(平均運動)は一定です。1太陽年で黄道を一周しますから、1日の平均運動は太陽年で割った値を使うことにします。
360度÷365.24219日=0.985647362度/日
春分の日は、1月1日から数えて79日目です。1月2日は春分の78日前になりますから、地球の黄経は
180-78×0.985647362=103.1195058
これが地球の黄経になりますし、仮平均地球の赤経になります。
地球の位置を赤経と赤緯に変換します。
赤経=104.2529327度 、赤緯=1.133426974度
が求められます。これから仮時差は、
103.1195058−104.2529327=-1.133426974度
=-4.533707895分
他の時差・均時差と同様平均値を求めてその値を引くことで
時差=-4.536374241分
が求められます。
最後にグラフを書かせます。たくさんの列を途中の計算に使っています。必要な列だけを別のシートに貼りつけてそこからグラフを書かせる方が簡単でしょう。 なお、欽一展通過時からではなく、元期(1月1日0時))からの計算をしています。 またグラフは、楕円軌道時差では元期からの計算結果を用いています。地軸傾きによる時差についても日にち(ケプラー運動の場合)にあわせています。 最初に載せたグラフはこの方法で書かせたものです。
ここまでの計算をした内容をxls形式のファイルにしています。
ここからダウンロードできます。zip形式に圧縮しています。
読みこみファイル名wisp18-08.zip サイズ253,952 バイト
解凍ファイル名 wisp18-08.xls サイズ627,200 バイト
2023.09.03 作 成
<ヨッシンと地学の散歩>
<<一つ前 次へ >>