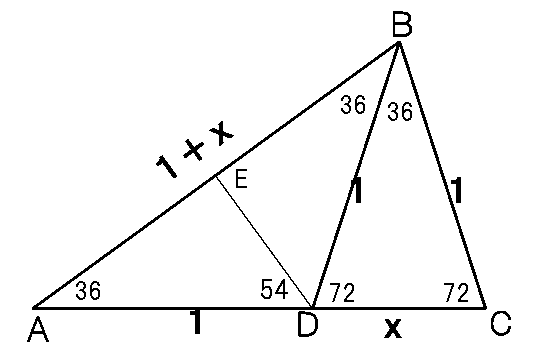秋の日はつるべ落とし
秋の日の暮れるようすを例えて「秋の日はつるべ落とし」というようにいわれることがあります。 「秋の釣瓶落し」のように言い回しかたが変わっている場合もあります。 このようすについて、検証してみることにします。 最初に、どういうことを示しているのかを考えてみます。まず「釣瓶(つるべ)」と「つるべ落とし」の意味でです。
「釣瓶」は井戸から水をくみ上げるための桶のことです。ところで、井戸そのものも最近見かけなくなりました。
右写真は、岡山県真庭市勝山で見かけたものです。たくさんの釣瓶が並んでいます。
最初に、どういうことを示しているのかを考えてみます。まず「釣瓶(つるべ)」と「つるべ落とし」の意味でです。
「釣瓶」は井戸から水をくみ上げるための桶のことです。ところで、井戸そのものも最近見かけなくなりました。
右写真は、岡山県真庭市勝山で見かけたものです。たくさんの釣瓶が並んでいます。これを使って水を汲むときは、持ち手の部分に縄をつけて井戸の中に落とします。 桶が水の中に浸かったところで、縄を引っ張りあげ桶を中に入った水ごと回収します。
桶をそのまま水面に落ちても桶はそのまま浮かんでいるだけで水が入ってきませんから、 重りなどをつけて水が入ってきやすくなるようになっています。 釣瓶を井戸の中に落とすとき、かなり速い速度で落ちていきます。重たくなっている分だけ途中で止めるのは大変です。 手に持った縄の感触ではもっと速く感じられます。
このことから「つるべ落とし」は速く落ちていくという感じがするときの例として使われているようです。
次に、「秋の日はつるべ落とし」について考えてみます。
日が落ちていくということは、日が沈んでいくことを指しているのでしょう。 それが速く感じられるということです。ところが、日が昇ったり沈んだりする速さは1年を通じてほとんど変わりません。 1日の長さは変化します。それは大きくても1分は越えないでしょう。24時間の内の1分ですから、違いはわかりません。
それでは、何が速いのでしょうか。速く感じるのは、そのものの動く速さが確認できる場合です。 実際には太陽が動いているのをほとんど感じることができません。わかるのは、ある時間たった後で場所を比べてみることで動いていることがわかります。 たとえば、日が沈むとすぐに真っ暗になりません。しばらく薄暗い時間が続きます。これを黄昏時とか薄明とかいいます。 この時間が短ければどうでしょう。日が暮れるのがはやかった、ということになるでしょう。 この場合の「はやい」は「早い」で表されますが、実質上同じ意味でしょう。
実際に、暗くなるまでの時間がどう変わるかを検証してみます。 計算にあたっては大気差の影響は無視することにします。また、日没とは太陽の上端が地平線に接したときと定義されていますが、 簡単にするため、太陽の中心(太陽が非常に小さいとして)で考えることにします。
<薄明時間の変化を求める>
時間を求めようとする前に、確認しておかないといけないことが一つあります
なにかというと、薄明(黄昏)はどういう状態になるまで続くのかという問題です。
一般的にいわれているのは、太陽の中心の高さ(高度)がある角度になるまでとされています。
この角度は見る人によって、変わってきます。ぜんぶで4種類あります。
まず、周りの景色がわからなくなるまでの時間帯です。これは地平線の下6度になるまで続きます。この時間帯は常用薄明といいます。
次のものは、昔の時の測り方か来たものです。日暮れまでの長さは2刻半とされていました。
1日の長さの40分の1にあたります。今の時間でいうと約36分になります。京都では、この時刻には太陽は地平線下7゚21'40"にあります。
3番目は、船に乗っているときに水平線がわかる明るさの時間帯です。太陽は12度沈んでいます。これを航海薄明といいます。
最後です。星を見るときに明るさの影響を受ける時間帯です。太陽が18度沈むまで続きます。これを天文薄明といいます。それでは、図を書いて考えてみることにします。このあたりの説明は不要だという人は読み飛ばしてもらっても結構です。 でも、できたらつきあってください。三角関数が出てくるので無理にとは言いません。読み飛ばし先は ここです。
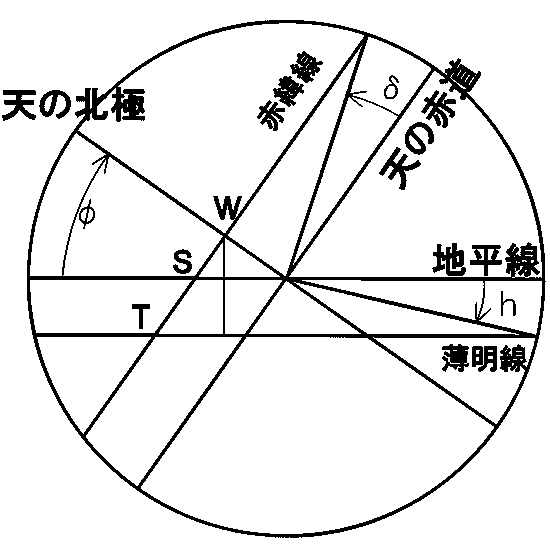 右の図は、天体の動きを考えるときに書かれる「天球」を真西の事情に遠いところから見たようすです。
星や太陽の動き(日周運動)がどのようになるかを考えるときは、天球が天の北極と天の南極を結ぶ線を軸(極軸)として回転しているものとします。
極軸は、地平線からその地点の緯度と同じ大きさだけ傾いています。緯度はφで表します。
天の北極と天の南極の真ん中が天の赤道です。この図では2点の垂直2等分線になります。
右の図は、天体の動きを考えるときに書かれる「天球」を真西の事情に遠いところから見たようすです。
星や太陽の動き(日周運動)がどのようになるかを考えるときは、天球が天の北極と天の南極を結ぶ線を軸(極軸)として回転しているものとします。
極軸は、地平線からその地点の緯度と同じ大きさだけ傾いています。緯度はφで表します。
天の北極と天の南極の真ん中が天の赤道です。この図では2点の垂直2等分線になります。太陽の位置は、春分・秋分の日は天の赤道上にいます。それ以外の時期は天の赤道から離れた位置にいます。 どれだけ離れているかを赤緯で表します。記号はδを使います。図には、赤緯δの天体が1日の間に動く線を赤緯線で示しています。 天の赤道と赤緯線は、この図では平行線になります。
太陽がここまで沈むと薄明が終わるという線を薄明線として記入しています。この線は地平線と平行線で表せます。 この時に太陽の沈んでいる角度をhとします。常用薄明を用いると、h=6度になります。
※ 普通hは上向きに測ります。これだと−がつきます。省略するために下向きに測ることにします
赤緯δの太陽が赤緯線に沿って動いたとします。図で極軸と重なってみえる点をWとします。 実際には重なっていません。太陽が南中してからここに来るまで6時間かかります。 赤緯線と地平線、薄明線が重なっているところを、それぞれS、Tとします。日没時、薄明終了時の太陽の位置になります。
また、太陽がWを通過してから、SやTに達するまでの時間をtS、tTとします。 時間で表されていますが、太陽は1時間に15度と決まった速さで動きます。 そのため、この時間の間に動いた角度を意味することもあります。
図から直接薄明の起こっている時間を求めることはできません。 tS、tT(角度)が求められれば、差を取れば薄明の起こっている時間になります。 この2つは求めることができます。順番に求めていくことにします。
まず、tSです。図上では、WSの長さは赤緯線の長さの半分のsin(tS)倍になっています。 赤緯線の半分の長さは、天球の半径を1とするとcos(δ)になります。したがって次の式をつくることができます。
WS = cos( δ ) × sin( tS )
また、この長さは、天の赤道と赤緯線の間隔の
WS = sin( δ ) × tan( φ )
2つの式から
cos( δ ) × sin( tS ) = sin( δ ) × tan( φ )
sin( tS ) = tan( δ ) × tan( φ )
tS = asin{ tan( δ ) × tan( φ ) }
を求めることができます。
次にtTを求める式を作ります。 Sの場合と同じようにしてWとTの長さは次のようになります。
WT = cos( δ ) × sin( tt )
ここで、Wから薄明線に降ろした垂線の長さを考えてみます。
垂線の長さ = WS × cos( φ )
= cos( δ ) × sin( tt ) × cos( φ )
になります。また、地平線との交点を境にして上半分と下半分に分けて求めることもできます。
ここで、上半分の長さは天の赤道と赤緯線の間隔の
また、下半分は薄明線と地平線の間隔ですから、
以上をまとめると
垂線の長さ = sin( φ ) × sin( δ ) + sin( h )
になります。これは先ほどの式と同じ長さです。右辺どうしを等号でつなげると次のようになります。
cos( δ ) × sin( tt ) × cos( φ )
= sin( φ ) × sin( δ ) + sin( h )
sin( tt )
={ sin( φ ) × sin( δ ) + sin( h ) }
÷ cos( δ ) ÷ cos( φ )
ttは、最後の式の右辺のasinをとれば求められます。長くなるのでここでは省略します。 これでtSとttが求められました。
求めたい薄明時間は2つの値の差を取ることで計算できます。
計算で薄明時間を求めました。三角関数、逆三角関数の入った複雑な式になりました。 関数を使わないで求めようとすると、次に考えられる方法は図を書いて求めてみる方法になるでしょう。 やってみます。
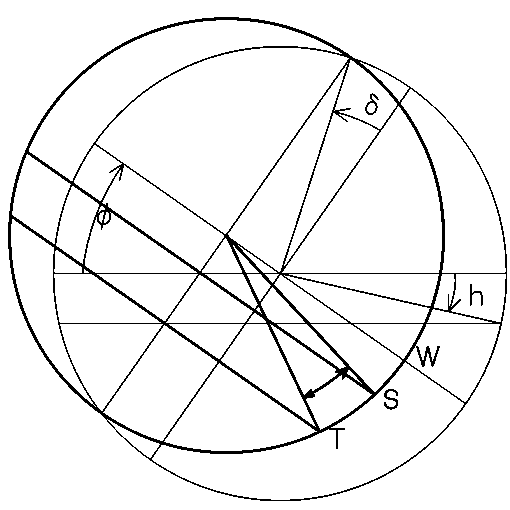 作図するといっても計算をした場合と同じ手順でやっていけば、求める答えにたどり着けるでしょう。
計算をするために書いた図はそのまま使うことにします。知りたいのはWSやWTに対する中心の角度です。
この部分だけ追加して書いてみます。
作図するといっても計算をした場合と同じ手順でやっていけば、求める答えにたどり着けるでしょう。
計算をするために書いた図はそのまま使うことにします。知りたいのはWSやWTに対する中心の角度です。
この部分だけ追加して書いてみます。WSTの点や中心角といったものは、赤緯線の作る面上にあります。 この面は、赤緯線上で図面から垂直にたった状態であります。これを面の交線の位置をそのままにして倒した図を書くことにします。 それが右図です。今までの図にあった線を細くして、新たに引いた線は太くしています。
WSTの点は新しく描いた円の上にありますから、移動させています。 図の中で、矢印で示した角度(を回転するのに要する時間)が薄明時間になります。
 これで答えが出たように思えますが、1つ大事なことが抜けています。
このままでは太陽の赤緯がわからないことです。これも計算で求めることにします。
これで答えが出たように思えますが、1つ大事なことが抜けています。
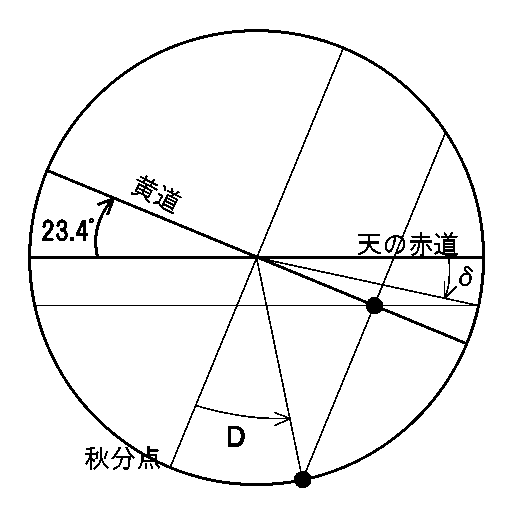
このままでは太陽の赤緯がわからないことです。これも計算で求めることにします。天球を秋分点側から見た図を考えてみます。天の赤道は傾ける必要はないので、水平にしています。 太陽の通り道を黄道といいます。黄道と天の赤道は23.4度で交わっています。交点が秋分点です。
太陽がどう動くかを考えるために、黄道の作る面と図面の交線のところで倒した図を考えてみます。 天球を上少し右側から見た図になります。 外周の円の位置は変わりませんが、秋分点の位置が示した位置までずれます。
太陽はこの円上を1年かかって1周する速さで左回りにまわっています。D日後の位置を円周上に黒丸で入れてみました。 この時の秋分点方向からの角度もDとします。D日を角度に換算するには365で割ってから360倍すれば求められます。
黄道の円を元通りに立ててみます。太陽の位置は黄道と書かれていた線の上まで移動してきます。 もとの秋分点からsin(D)だけ離れた位置にあります。
ここで黄道面を倒した図は忘れてください。その上で、太陽が天の赤道からどれだか離れた位置にあるかを考えます。 求め方は2通りあります。赤緯に注目するとsin(δ)になります。黄道上の位置から考えると、sin(D)のsin(23.4度)倍ともいえます。 両者は同じ大きさですから、等号でつないで
sin( δ ) = sin( D ) × sin( 23.4度 )
δ = asin{ sin( D ) × sin( 23.4度 ) }
という式を作ることができます。
計算式ができました。この式は微分して最大最小の位置や大きさを求められそうもありません。 表計算ソフトで毎日の薄明時間を計算させてグラフに書かせてようすを見ることにします。 北緯35度の地点での計算結果の表とグラフです。計算結果は何分かを示しています。
| 日数 | 常用薄明 | 日暮れ | 航海薄明 | 天文薄明 | グラフ |
| -105 | 34.1 | 42.0 | 70.3 | 110.2 | 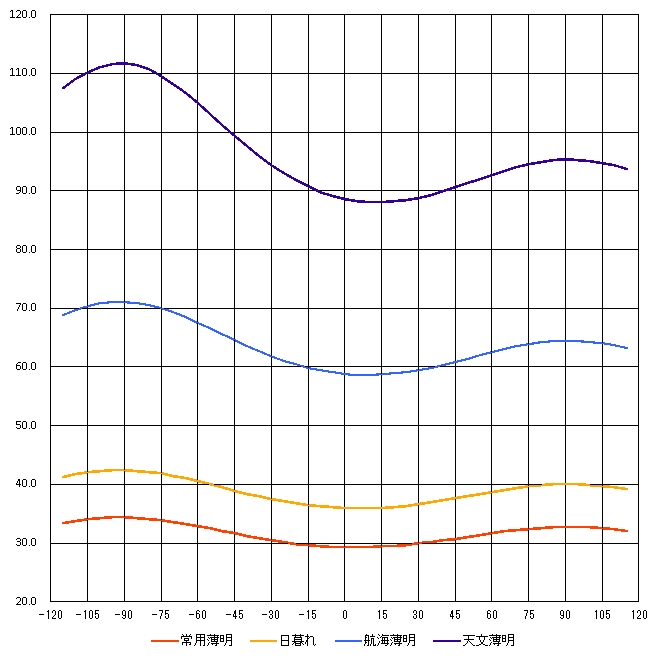 クリックで拡大します
クリックで拡大します |
| -90 | 34.4 | 42.4 | 71.1 | 111.7 | |
| -75 | 33.9 | 41.9 | 70.0 | 109.6 | |
| -60 | 32.9 | 40.5 | 67.5 | 104.9 | |
| -50 | 32.1 | 39.5 | 65.5 | 101.2 | |
| -40 | 31.2 | 38.4 | 63.6 | 97.6 | |
| -30 | 30.5 | 37.5 | 61.8 | 94.4 | |
| -20 | 29.9 | 36.7 | 60.4 | 91.8 | |
| -15 | 29.7 | 36.5 | 59.9 | 90.7 | |
| -10 | 29.5 | 36.2 | 59.4 | 89.9 | |
| -5 | 29.4 | 36.1 | 59.1 | 89.2 | |
| 0 | 29.3 | 36.0 | 58.8 | 88.7 | |
| 5 | 29.3 | 35.9 | 58.7 | 88.3 | |
| 10 | 29.3 | 36.0 | 58.7 | 88.1 | |
| 15 | 29.4 | 36.0 | 58.7 | 88.1 | |
| 20 | 29.5 | 36.2 | 58.9 | 88.2 |
xls形式の表をダウンロードできます。緯度が変わるとどうなるかを試すこともできます。 ダウンロードする ←クリックしてください zipで圧縮しています。 (wisp16-06.zip; |
| 30 | 29.9 | 36.6 | 59.5 | 88.8 | |
| 40 | 30.5 | 37.3 | 60.4 | 89.9 | |
| 50 | 31.1 | 38.0 | 61.4 | 91.3 | |
| 60 | 31.7 | 38.7 | 62.5 | 92.7 | |
| 75 | 32.5 | 39.6 | 63.9 | 94.6 | |
| 90 | 32.8 | 40.0 | 64.5 | 95.4 | |
| 105 | 32.6 | 39.8 | 64.1 | 94.8 |
日数は秋分の日の何日前か後かを示しています。0が秋分の日で。−だとその前になります。−90(正確には−91.25)は夏至、 90は冬至の日にあたります。
表やグラフからわかることは、秋分の頃は日が沈んでから暗くなるまでの時間が短いということです。 一般的な常用薄明で考えてみます。数値で見ると、1ヶ月前に比べて1分半短くなっています。30分強に対してですから、 薄明時間の5%ほどの差です。これがわかるかどうかは微妙なところです。
「つるべ落とし」が、薄明の時間が短いということをいっているのだとすると、別の問題が発生してきます。 表を拡張して作って見るとわかることです。春分の頃も秋分と同様薄明時間が短くなります。 春分の頃のグラフは、秋分の時のグラフを左右逆にした形になります。これで考えてみてもいいでしょう。
どうして春はつるべ落としではないのでしょうか。冬の間はあまり外に出ないのでみていないということでしょうか。
2019.02.20 ここまで作成
<夕暮れ時間の変化を求める>
日が沈む前から、周囲は薄暗くなりはじめます。この時間から考えるともう少しようすがかわってきそうです。
暗くなり始めて、日中の仕事の片付けを始め、一段落したところで周囲をみると暗くなっていた、あるいは日が沈みかかっていた
ということはありそうです。
つるべ落としというものが実感できるのは、こういうときに起こりそうです。日がつるべ落としのようだとするなら、日が落ちていく速さを指しているように思えてきます。 それなら、日が沈んでからを考えるのはよくなさそうです。
ところで、この時間帯はなんと呼んだらいいのでしょうか。よく使われる言葉に、「日暮れ」あるいは「日暮れ時」があります。 「日が沈む頃」だそうです。これだと、日が沈んでからは含まれそうにないので、求めている言葉にぴったりきそうです。 広辞苑などを見ていると、これ以外にも常用薄明(の終了時)を明らかに指している語意も並べてあります。 あまりしっくりとはこない解釈です。無視したくなります。
「夕暮れ」「夕暮れ時」を引いても同じ意味が書かれています。意味合い的には、夕方のという時間帯が強調されていそうです。 太陽高度が低くなってから太陽が沈むまでの時間帯は、ここでは「夕暮れ」と呼ぶことにします。
どのようになっているのかは、夕暮れ時間を求めてみるとはっきりするはずです。 計算を始めようとしたのですが、「夕暮れ」がはっきりしていない以上に、その開始がいつになるのというのかということについて、 触れられているものは全くありません。
はっきりしているのは、太陽高度が低くなるにつれその光は弱くなり、その分暗くなっていくということです。 地面に当たる光の強さは、太陽高度の正弦(sin)に比例します。ある程度太陽の高さが低くなったら、夕暮れが始まると見ていいでしょう。 どれくらいになったら、うす暗くなった感じ始めるのかと示しているものはありません。
感覚的には、10度くらいになるとかなり暗くなっているように感じます。そもそも、夕暮れという言葉もはっきりしていませんから、 ここでは割り切って、一度出てきた7度21分40秒(常用薄明の水平線下仰角)と同じ数値を使うことにします。 この高さになると夕暮れが始まることにします。
ここまでで、薄明時間を計算するための表を作っています。太陽高度に-7゚
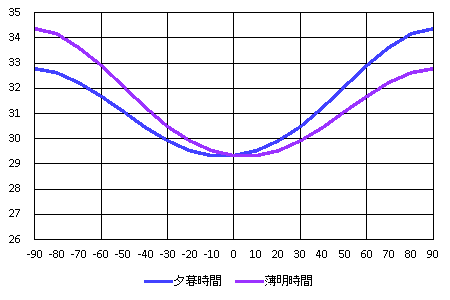 結果を右のグラフに示します。青線が夕暮れの時間、比較のために紫線で常用薄明時間を記入しています。
縦軸がそれぞれの時間(分)、横軸が秋分の日からの日数です。縦軸目盛が26分から35分の間という点に注意してください。
結果を右のグラフに示します。青線が夕暮れの時間、比較のために紫線で常用薄明時間を記入しています。
縦軸がそれぞれの時間(分)、横軸が秋分の日からの日数です。縦軸目盛が26分から35分の間という点に注意してください。前の日との薄明時間の差を考えてみます。数値が大きく、薄明時間が一気に(というほどでもないが)短くなっていくのは、 秋分の前1ヶ月から2ヶ月の間です。この頃の方が、暗くなるのが早くなったと感じやすいのではないでしょうか。
2019.09.22ここまで追加掲載
<日没時刻・薄明終了時刻の違い>
ここまでは、太陽が沈んでいく速度に関係して、薄明とか、夕暮れとかの時間がどれだけ短くなるのかを計算してきました。
その結果は、その時間は短くなるもののそれほど大きな変化はないということと、
春にも同じ現象がほぼ変わりなく起こるというものでした。あまり釣瓶落としという印象を受けません。そこで、視点を少し変えてみることにします。釣瓶が落ちていくときのようすを考えてきました。 そうではなく、井桁に乗せていた桶がいつの間にか中に落ちていたというのならどうでしょうか。 この場合、桶が太陽になります。釣瓶は桶につながっているので、一体と見なします。 桶だけだとどこかに行ったになりそうですが、釣瓶が垂れ下がっているのを見ると中に落ちたのだなというのがわかります。
日没の時刻や薄明終了の時刻を調べてみることにします。 薄明終了時刻は日没時刻から薄明時間後なのでとりあえず日没時刻を計算することにします。
今までに太陽が南中してから地平線に達する時刻は計算しています。 ところが実際の日没時刻や薄明終了時刻はこの時刻からずれます。 その原因のひとつは経度の違いによるものです。標準子午線のある明石から東に行けば日没や南中時刻は早くなりますし、 西では遅くなります。そのずれの大きさは毎日同じですから、日常の習慣として身についていると思われますから考えないことにします。 とりあえず計算上は明石(東経135度)で考えることにします。
日没時刻が今ままでしてきた計算からずらす原因となるものはもう一つあります。それは均時差という現象です。 均時差については、「均時差を求めてみた」で説明しています。 均時差について知りたい方はそちらを見てもらうことにして、ここでは話を先に進めさせてもらうことにします。
均時差を求める方法としては色々あります。均時差説明ページを利用するのもその一つです。 ここでは国立天文台暦計算室のページの正午と南中時刻のずれを利用することにします。 まず国立天文台暦計算室のこよみの計算cgi版を開きます。地点の指定方法で経緯度を指定にして経度を135度にします。 計算日時は、2010年1月1日に設定し、下のオプションで1日おきに1年間ボタンを押します。 指定できたら日の出入り南中時のgoボタンを押してでてきた一覧表を利用します。
国立天文台暦計算室のこよみの計算cgi版のurlは以下の通りです(2023年9月閲覧)
https://eco.mtk.nao.ac.jp/cgi-bin/koyomi/koyomix.cgi
なお日付を2010年に設定したのは、この年の秋分時が9月23日12時9分なので、正午とほとんど同じで 求めた値が秋分時を起点とした値にほぼ一致しているとみなせるからです。
ここに、日没時刻も記載されています。均時差の大きさを知ることによって他の地域での日没時刻も計算できますから あえて日没時刻の値を見ない事にしておきます。日没の定義が少し違いますから、計算結果も少し違っています。
100.5434-103.1093+0.9856091/8=-2.5695
入れるのは、計算結果でもいいですし、式でもかまいません。式の場合は平均運動の値の代わりにセル番号を示すC1を入れることもできます。 1ヵ所、均時差(角度)が360度を超えるところがありますから、このセルの式の最後に−360を加えてください。
計算結果の一例です。9月1日から5日ごと1ヶ月分の値です。均時差の単位は秒です。均時差2は表計算ソフトの出力結果です。 2秒ほど値が小さくなっています。
| 日付 | 南中時刻 | 均時差 | 均時差2 |
| 2010/9/ 1 | 12:00:09 | -9 | -10.1 |
| 2010/9/ 6 | 11:58:31 | 89 | 87.8 |
| 2010/9/11 | 11:56:48 | 192 | 191.0 |
| 2010/9/16 | 11:55:02 | 298 | 297.3 |
| 2010/9/21 | 11:53:14 | 406 | 404.1 |
| 2010/9/26 | 11:51:29 | 511 | 509.0 |
| 2010/10/1 | 11:49:49 | 611 | 609.5 |
日没時刻は、太陽高度が最も低くなる時から南中するまでの時間(12時間)と太陽が南中してから西の地平線に達するまでの時間の合計 から均時差を引いたものになります。南中してから地平線に達するまでの時間はすでに求めています。均時差も今求めたところですから、 すぐに求めることができます。
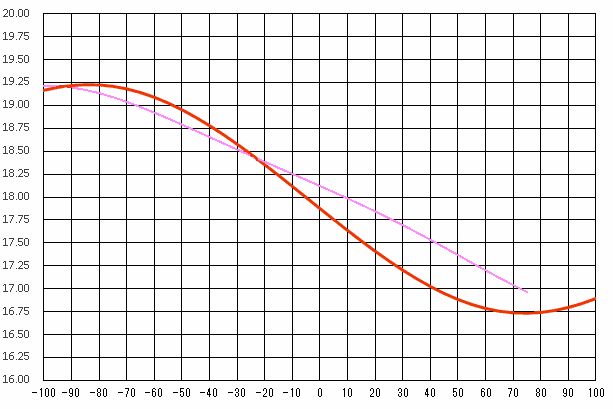 北緯35度東経135度の地点での日没時刻を求め、その結果をグラフにしてみました。
横軸は、秋分の日からの日数で、縦軸が時刻です。18.25は18時15分を示しています。
春分前後の日没時刻も日付を逆にして桃色線で入れてみました。
北緯35度東経135度の地点での日没時刻を求め、その結果をグラフにしてみました。
横軸は、秋分の日からの日数で、縦軸が時刻です。18.25は18時15分を示しています。
春分前後の日没時刻も日付を逆にして桃色線で入れてみました。秋分の日の前後1ヶ月の間は、10日経つと日没時刻は15分ほど早くなっています。 夕方の6時頃といえば、仕事が終わって帰路についたり、夕食の時刻です。だいたい時刻にあわせて行動しているので、 15分早くなっても気がつきそうな感じがします。つい先日までは駅に着いたときは明るかったのにもう薄暗くなっているとかで、 急速に日没が早くなっているのを感じやすくなっているといえます。
春分の頃の日没の変化のようすはこれに比べて半分くらいで、かなりゆっくりしています。 日が長くなってきていると感じるのは、秋に比べてはそうとう鈍くなりそうです。
ここまでの結論です。「秋の釣瓶落とし」というのは、日没時刻が急速に早くなり、気がついたら太陽が沈んでいたようすを、 いつの間にか井戸の中に釣瓶が落ちていたようすになぞらえていっているのではないでしょうか。
だとしたらこの言葉は、時計が一般に普及するようになってから使われるようになったと考えられます。 夕方のお寺の鐘の音と比べてというのもあるのかも知れません。明治以前には使われていなかったことも考えられます。 このあたりはどうなのでしょう。
秋分の日前後で均時差の1日あたりの変化は20秒以上あります。年によって同じ日でも早く沈む年と遅く沈む年とでは 最大でこ20秒違ってきます。それでも日没時刻の変化のようすは、ほとんど変わりません。 だいたいこれくらいの値たという目安程度で見てください。
先に太陽は、黄道上を一定速度で進むとして赤緯を計算しましたが、平均太陽は赤道上を一定速度で進んでいます。 赤緯の値は微妙に違ってきます。さらに厳密にいうと視太陽の位置のずれによる赤緯差も考慮する必要があります。 実際には、その赤緯差による日没時刻のずれよりも、均時差の1日あたりの変化の方が大きいので無視することができます。
2020.09.20この部分 掲載
2023.09.xx 一部加筆修正
2023.09.xx 一部加筆修正
<薄明時間を決めるもの>
薄明時間がどれくらいあるのかということが書かれているものを調べてみると、太陽高度との関係について触れられているのがほとんどです。
ここまでは、その記述に沿って考えてきました。ここからはもう少し深く探っていくことにします。そもそも薄明はどのようにして生じるのでしょうか。いま太陽が沈んだとします。地面の上は太陽の光で照らされていません。 ところが、上空はまだ日が当たっています。このようすは、高い山や空にある雲がまだ太陽に照らされていることからわかります。
上空に太陽の光が当たっていると、そこにある空気によって散乱したり反射したりすることで、空が明るく見えることになります。 これが薄明の原因となっています。
地球の大気は上空ほど薄くなっています。その分、散乱や反射によって光る量は少なくなっていきます。 太陽が深く沈んでいき、この上空の空気しか照らさなくなることによってだんだんと空が暗くなっていきます。 これが一定量以下の明るさになったときが薄明終了といえます。
それでは、どれくらいの高さが照らされなくなったときに薄明終了となるのでしょうか。 計算しようとしましたが、1つ問題につきあたります。東の空と西の空では、太陽の光が当たっていない最高点の高さが違っています。 その分空の明るさも違うようです。薄明が時間や太陽高度で決められている以上は方角によって明るさが違うのは特に問題はなさそうです。 どの方角でもその時の暗さになったときが薄明終了と定義し直せばいいだけの話です。 とりあえず、いちばん明るく見えそうな西の地平線近くでの暗さを基準にする事にします。
暗さはどれくらいの高さより高いところしか照らされていないかで決まってきます。この高さを求めるのがよさそうです。 常用薄明(太陽高度−6度)について、西の地平線に見える大気が照らされていない最高点の高さを求めてみます。
とりあえずこの場所をAとします。Aから見たときに、観測者のいる場所、日没になっている地点はどちらも地球への接線の交点になります。 接線は6度で交わっていますから、Aから両地点は水平線から、3度(6度の半分)下に見えることになります。
このことから、Aの地表からの高さは次の式で計算できることになります。
地球半径÷cos(3度)−地球半径
計算結果は、約8800mになります。圏界面よりも少し低いくらいで、300hPaの高度がだいたいこれくらいになります。
一般的に、圏界面より下層は対流圏と呼ばれ、大気の上下運動が盛んにおこなわれている場所です。 大気の上下運動によって運ばれてきた水蒸気が凝結したり、塵などが舞い上がったりする条件がそろっています。 そのため、大気中には小さな粒子がたくさん含まれ、大気による散乱反射は強そうです。 これに対して、この上の成層圏は大気が安定していて、水蒸気の凝結はなさそうだし、塵なども下方に落ちていってなくなりそうです。 大気はあまり光らないでしょう。圏界面の上下で大気の明るさに差ができそうです。
気圧はそこよりも上空にある大気の量を表しています。 このこともあわせて考えてみると、常用薄明の定義を次のように書き換えてみるのもよさそうです。 高層気象では高さは気圧で表すことがあります。空の明るさで考えるとほとんど同じことになります。
西地平線延長上で300hPa面より低い所が照らされなくなるまで
ところで、300hPaの高度は日によって変化します。(上空の)高気圧に覆われると高くなるし、低気圧の接近で低くなります。 このようすは、気象庁が発表する高層天気図(AUON30)で確認することができます。 一般的には夏は高度が高く9700mくらいで安定しているのに対して、秋から冬にかけてだんだん低くなっていき、 真冬の本州南部で9000m、北海道だと8500mくらいになります。 当然300hPa高度が高くなれば薄明時間は長くなるし、低くなれば短くなります。
この高度の違いによって、薄明時間がどれくらいになるかを計算してみることにします。先ほどの式の逆で計算することになります。 結果は9700mだと太陽高度は−6.30度、9400mで−6.20度、9000mで−6.07度です。 北緯35度地点での秋分の日の薄明時間になおすと、それぞれ30.8分、30.3分、29.6分です。 最大でも差は1分ほどです。この大きさは太陽の動きに関係して起こる常用薄明の時間短縮の大きさとほぼおなじです。 2つあわせて効果は大きくなるものの、これだけではまだ「釣瓶落とし」といえる程の速さとはいえないでしょう。 日没時刻や薄明終了時刻が早くなる効果としては小さいようです。
薄明時間が大気の高さで決まるのであれば、大気の状態によっても変わってきそうです。 乾燥していて空気の透明度の大きいときと、湿っていてもやがかかっているような状態では違ってくるのではと思われてきます。
実際にどのように影響があるのかわかりません。そこで、写真を撮って比べてみることにしました。 一定時間毎に同じ条件で連続して撮影し短冊状に切り抜いたものを並べてみます。 撮影日は2021年4月5日と10日です。 日没7分前から2分間隔で撮影し、切り出し場所は最初の1枚の下端に太陽が入る場所で固定しています。 1枚目のみ、ND400フィルターを装着し適正露出になるようにしています。 並べた写真の枚数は20枚で、38分間の記録です。日没後約30分までですから、だいたい常用薄明が終わる頃までの記録になります。
撮影条件は、f=82mm(フルサイズ換算)、F5.6、1/60sec、ISO400です。


2枚の写真を見比べて見ると、10日の方が空が暗くなるのが明らかに早いということです。 5日では露出オーバーで白くなっている所がだんだんと暗くなり、適正露出になるまで20分(10枚)程かかっています。 これに対して、10日では日没(3枚目と4枚目の間が日没時刻)ころから空が暗くなり始めています。
10日では、その後しばらくの間空が暗くならないようです。この時間帯はまだ1万m位の高さでは太陽の光が当たっています。 日没後15分くらいから光の当たらないところが急速に広がりますが、 次第にゆっくりしてきて地平線付近では30分くらいまで続くようです。 それでも空の明るさは、地平線近くをのぞいては10日の方がはるかに暗いといえます。
太陽高度によって照らされているところの仰角(天頂角度)はこちらで計算しています。
時間への換算は先の薄明時間の計算式に代入して求めています。カメラの焦点距離から見ると写真の上端の仰角は16度くらいなので、
影の広がりがゆっくりし始めた頃の部分が写っています。これでも速いときよりはゆっくり広がって写っているようです。
この違いはどうして起こったのでしょうか。気がつくのは、5日は雲らしきものがないのに対して、
10日では巻雲が広がっているということです。巻雲といえば秋を象徴するような雲です。
10日は秋の空が暗くなるようすを代表的に表していると見ていいでしょう。これに対して、5日は夏の空と見ることができます。夏から秋になると、薄雲が広がってくる事が多くなり、その影響で空が暗くなるのが早くなると見ていいでしょう。 これと日没時刻が早くなる効果があわさって暗くなるのが急速に早くなるといえます。これが釣瓶落としの理由と考えるのはどうでしょうか。 それが、夕食の準備時刻や仕事の終了時刻にかかかってくると、もうこんな時間となりそうです。 さらにいうと、夏には少ない、完全に曇りや雨の日には日没前から暗くなっています。さらに早くなったと感じるのではないでしょうか。
2021.12.16 この部分 掲載
西から太陽を昇らせる
中学生が西から太陽が昇ってくるように見えるにはどうすればいいかという研究発表をしたということで話題になっていました。
研究内容まで発表されていませんので、詳しく知ることはできていません。
エレベーターで上にあがっていくと再び太陽が見えるようになるという内容のようです。ここでは、どのようにすると太陽を昇らせていくことができるか、それぞれの方法について詳しく検証していくことにします。
<高速で上昇する>
地表付近で日が沈んでいても、同じ場所で高さが違えばまだ沈んでいないことがあります。 このあたりのようすは別のページ (以後「丸い地球のページ」と呼ぶことにします)にも書いています。 山の斜面を地球の影が登っていくよりも速く上昇していけば、一度見えなくなった太陽が再び見られるようになります。 それでは、どれくらいの速度で上昇していけば、再び昇ってくるのでしょうか。いろいろ計算してきましたので、簡単にできそうです。 詳しく求めてみることにします。
これは簡単に解けるだろうと思っていました。実際にやってみると、大問題に突き当たります。 そこから説明していくことにします。
「丸い地球のページ」に書かれている太陽高度(−θrad)と影の高さ(Hm)の関係式は次のようになっています。 Rは地球の半径(km)です。
13 × H = ( R × θ )2
太陽が沈んでいく速さは、日没前後のわずかな時間の間なら一定と考えていいでしょう。 それなら、角度は時間に比例します。時間をtとすれば比例定数Kを使って、θ=Ktと書くことができます。 これを先ほどの式に代入して、
13 × H = ( R × K × t )2
時間(t)で微分すれば速さ(V)が求められます(Hをtで微分したものがVです)。結果は
13 × V = 2 × R × K × t
となります。
| ※ | 高度と影の高さ(時間)の関係式は、等加速度運動(初速度0)の時間と距離の関係式と同じです。 したがって、影の運きは等加速度運動と考えることができます。この場合、速度は時間に比例します。 計算と同じ結果を示しています。 |
ところで、この式のtに0(日没の瞬間)を代入すると、速度は0になります。 このことからいえるのは、日没した瞬間に上の方に移動していれば、影を追い越すことができるということです。 壁を登っていくカタツムリだって、再び太陽を見ることができることになります。 実際には太陽を見る時間はほんのわずかなのでしょう。これでは、計算をする意味がありませんから、 求めたいものを変えてみることにします。
| ※ | 影の長さを求める式は、中心角θだけ離れたところを通る円の接線が、その地点の真上どれくらいの距離のところで交わるかを求めています。 θが0の場合は接点と地点は重なるために距離は最小の0になります。最小値をとるということは長さの変化率(この場合は速度)が0だということです。 速度が0になることは、計算しないでもわかることでした。 |
日没の瞬間に一定速度で上昇し始めたとします。再び太陽が顔を出します。 みていると太陽は地平線に近づき、かくれてしまいます。再び日が沈んだように見えます。 この時間はどれくらいあるのでしょうか。あるいは、その高さはどれくらいなのでしょうか。といったところが疑問点になりそうです。 普通こういう現象が見られそうなのは、エレベーターで高い建物を上がっていくときくらいでしょう。 それなら、日没瞬間に上昇し始めたエレベーターが最上階に着いたときに太陽が見えている場合の最低速度はどれくらいかとしても良さそうです。 乗り物はロープウェイでも飛行機でもなんでもいいので限定を外します。どちらかというと建物の高さで限定されそうなので次のようにする事にします。
日没の瞬間に地表から一定速度で上がり始めたときに、ある高さで太陽を見るための上昇速度は最低でいくらか
| ※ | 太陽は大きさを持っていますから考慮すると複雑になります。 点光源であるとか中心といった太陽内の決まった場所として考えることとします。 |
- - - - - - - - - - - - - - - - - - - - - - -
本節の前半で太陽高度とそこまで沈む時間の関係式を作っています。 表計算ソフトにも式を入れていますから、これを拡張することにします。 また、太陽高度と影の高さの関係式は「丸い地球のページ」のものを使うことにします。ソフトで使った表を新しいページにコピーして薄明高度の欄を高さから太陽高度を求める式に書き換えます。 その他多少変更するところはありますが、計算結果は下の表のようになります。北緯35度での値です。 地表での日没後太陽が沈むまでの時間(分)と影に追い越されない最低速度(m/分)を書いています。
「丸い地球のページ」の式は有効数字2桁なので、ここまでの精度はありません。だいたいの目安として見てください。
| 日\高さ | 0 → 100 | 0 → 300 | 0 → 600 | 0 →1000 |
| 夏至 | 1.80 55.4 | 3.13 95.9 | 4.43 135.5 | 5.72 174.8 |
| -75 | 1.78 56.1 | 3.09 97.0 | 4.38 137.1 | 5.65 176.9 |
| -60 | 1.74 57.6 | 3.01 99.7 | 4.26 141.0 | 5.50 181.8 |
| -45 | 1.68 59.6 | 2.91 103.2 | 4.11 145.9 | 5.31 188.3 |
| -30 | 1.62 61.6 | 2.81 106.6 | 3.98 150.7 | 5.14 194.5 |
| -15 | 1.59 62.9 | 2.75 109.0 | 3.89 154.1 | 5.03 198.9 |
| 春分秋分 | 1.58 63.4 | 2.73 109.9 | 3.86 155.4 | 4.98 200.6 |
| 15 | 1.59 63.0 | 2.75 109.1 | 3.89 154.3 | 5.02 199.2 |
| 30 | 1.62 61.6 | 2.81 106.8 | 3.97 151.1 | 5.13 195.1 |
| 45 | 1.67 59.7 | 2.90 103.5 | 4.10 146.5 | 5.29 189.2 |
| 60 | 1.73 57.7 | 3.00 100.1 | 4.24 141.6 | 5.46 183.0 |
| 75 | 1.78 56.2 | 3.08 97.4 | 4.35 137.9 | 5.61 178.2 |
| 冬至 | 1.80 55.6 | 3.11 96.3 | 4.40 136.3 | 5.68 176.2 |
もっと高いビルではどうでしょう。エレベーターも速くなっています。高さ300mのあべのハルカス(360m/分)や 240mのコスモタワー(咲洲庁舎:180m/分)では、太陽を再び見るのにはじゅうぶん可能な速さです。 270m高いと太陽まるまる1個分浮き上がったようにみえます。再び太陽が見えたという感じがするでしょう。 残念なことに、どちらの展望エレベーターも東側を向くように設置されています。
計算で求めてきましたが、この方法では三角関数を使うなど中学生にはレベルが高すぎています。 条件を、特定の緯度と秋分春分の日没の瞬間に限定することで、式はもっと簡単になります。 中学生が解けるような範囲内でやってみます。
秋分春分の頃の太陽は真西の地平線上で沈みます。この時の角度は90度から緯度を引いたものになります。 太陽は1分間で0.25度進みます。この2つから1分間にどれだけ沈んでいくかを求めることができます。
普通ここでの計算は、三角関数[sin(90−緯度)またはcos(緯度)]を使います。 角度が限定されているので、三角形を作図し各辺の長さの比から求めることも可能です。これで三角関数を使わなくて済みます。 中学生は緯度を36に限定していたそうです。偶然だったのかも知れませんが、cos(36度)は数式で表すことができます。 36度の頂角を持つ直角三角形の斜辺に対する底辺の割合は、(root(5)+1)÷4です。 ここで、root(5)は5の平方根をあらわすものとしています。計算結果を数値にすれば0.809……です。
緯度を36度にしてみます。太陽の沈んでいく速度は
0.25×0.81= 0.20 度/分
です。
日没後t(分)経ったときの太陽の高さ(伏角)は
0.20 × t
で表せます。
ここで、「丸い地球のページ」の式に代入します。再掲します。
13 × H = ( R × θ )2
この式を作るには式の変形と平方根しか使っていません。使用できる範囲内と判断します。
このR×θは「どれだけ遠くが見えるか」では地平線(地球表面への接点)までの距離としています。 角度θは度の単位で測ったとして、距離(円弧の長さ)を求める式を代入して
13 × H = ( R× π ÷ 180 × θ )2
H = 960 × θ2
中心角と太陽高度(伏角)は同じになるので
H = 38 × t2
影がHの高さに到達する時間は
t2 = H ÷ 38
t = root( H ÷ 38 ) = root( H ) ÷ 6.2
が求められます。
これから影に追い越されない最低速度(V)は
V = H ÷ t = H ÷ ( root( H ) ÷ 6.2 )
= 6.2 × root( H )
となります。
この式から、100mの高さだと最低速度は62m/分、400mで120m/分、900mで190m/分 とだんだん大きくなっていくのがわかります。
上の方に上がっていくと、いったん沈んだ太陽が再び地平線の上にあがってくる条件を求めることができました。 ところで、この条件に従って昇ってくる太陽が見えたとします。どうなっているのでしょうか。 太陽の距離は非常に遠いので、見える方向は変わりません。変わって見えたのは地平線の方向です。 上の方に上がっていくにしたがって、地平線が下がっていき太陽のある所よりも低くなるなることで、太陽が出てきたように見えただけです。 これでは、本当に太陽が昇ってきたといえるのでしょうか。
たとえば、列車か船で移動しているとします。太陽は西の空に傾き始めています。 なだらかな山の斜面にかかると見えなくなります。遠くの山だと日が沈んだといえるでしょう。 列車や船が移動していきます。それにともなって山は後の方に動いて見えるでしょう。 山の反対側の斜面から太陽が再び顔を出すことだってあります。この場合は、太陽が昇ってきたといえるでしょうか。
高いところに登って太陽が見え始めたことを太陽が昇っていったとするのには少し抵抗を感じます。 ここでは、あくまでも「見えなくなった太陽が再び見え始める条件」を求めたということにしておきます。
2019.02.20この部分掲載
- - - - - - - - - - - - - - - - - - - - - - -
<西に移動する>日の沈む時刻は西側の地域ほど遅くなります。ある場所で日が沈んだとします。 そこから西へ進んでいき、その先の地点での日没時刻よりも早く到着できれば、太陽が昇っていくようすを見ることができます。
どれくらいの速度で進むといいのか求めてみます。太陽が西の地(水)平線上に見える状態になるような一定の速さで移動したとします。 ずっと進んでいってまる1日経つと元の場所に帰ってきます。進む速さは一定になります。24時間で経度360度分進みますから、 1時間で15度になります。 移動する経路は、同じ緯度上の場所、言い換えれば同一緯線上です。緯線の長さは緯度によって変わります。 緯度が小さくなるほど長くなり、赤道上では約40000kmになります。従って、赤道上では 時速40000
こんどは、北緯36度の地点を考えてみます。地球は半径6370kmの球形として、北緯36度の地点での緯線の長さは、
1 + root( 5 )
2 × π × 6370 × −−−−−−−−−
4
= 32400km
と求められます。
分数の部分はcos(緯度)を用いるのがふつうです。三角関数が使えないものとして三角比を用いています
24時間で割って、時速1350km、秒速で375m(音速よりちょっと速いくらい)になります。- - - - - - - - - - - - - - - - - - - - - - -
<北か南に移動する>同じ経度の地点でも、北と南では日没時間に差があります。西に進んだ時と同じように、一方が日没になってから、 他方が日没になるまでの間に移動すれば、再び太陽が昇ってくるように見えるでしょう。どれくらいの速度で移動すればいいのか求めてみます。
すでに各緯度で、決めた日の日没時間の計算式をつくっています。 ここから緯度が1度違えば、日没時刻はどれだけずれるかを求め、その時間で緯度差1度を移動する速度を計算することにします。 緯度差1度は、地球が半径6370kmの球形だとして111kmになります。これを日没の時間差で割ると速度が計算できます。
夏至から冬至まで15日おき、緯度は25度から44度まで1度ごとに計算してみました。計算結果を表に示します。 表は大きくなりますので、日付ごとに表示するようにしています。 日を変えるときは、「15日前<」または「>15日後」と書かれている場所をクリックしてください。
緯度の値は、その緯度から1度大きなところとの間で計算したという意味です。 負数になっている場合は、1度大きな地点から南に移動してくるときの値を示しています。 春分の日、秋分の日では同じ経度の地点は同時に日没になりますから、速度は無限大(∞)と標記しています。
2019.09.22ここまで追加掲載
2019.02.22掲載
2019.09.22加筆
2020.09.20加筆
2021.12.16加筆
2023.09.03加筆
2019.09.22加筆
2020.09.20加筆
2021.12.16加筆
2023.09.03加筆
<ヨッシンと地学の散歩>
<<一つ前 次へ >> -->