ヨッシンと 地学の散歩
散歩道の四方山話
散歩道の四方山話
夕立が起こった後などにできる虹はきれいです。ところで、虹の色は何色なのでしょうか。いくつか写真があるので見比べてください。こことここにあります。
虹の色は、赤色から紫色まで順番に少しずつ変化していきます。何色が含まれているかは断定しづらいところもあります。 色の種類については、国によって違うようなのですが、日本では、一般的には、赤・橙・黄・緑・青・藍・紫の七色が使われます。 いわれてみればそうかなとも思いますが、色がわかりづらかったり、別の色が見えたりすることもあります。
この色の組合せは、何かの規則に従っていると考えてみると、不思議に思うところがあります。。 というのは、1番目、3番目、5番目は色の3原色です。2番目、4番目、7番目はその中間色です。ところが、 6番目は、5番目の色を単に暗くしただけの色です。要するにこれだけ純色ではないのです。 そう思って虹をよく見ると、 藍色はわかりにくいような気もします。藍色はなぜ虹の七色に入っているのでしょうか。

虹の七色で、仲間はずれは、藍色だと思っていたのですが、本当は紫色なのではないでしょうか。 最近は、虹や虹のような模様を見る時、紫色があるかに注意してみるようにしています。
虹色ができる原理は、2通りあります。一つは、光の干渉を利用する方法、もう一つは、光の分散を利用する方法です。 一つめは、等間隔離れた場所から出た光の山や谷が、揃う方向では明るくなり、揃わない方向では暗くなる原理を使っています。 このとき、見る方向によって特定の色だけが光って見えます。レインボーフィルムや、CDディスク、 昆虫の羽根などが虹色に光っているのはこの原理によるものです。 自然現象ではどんなものがあるかについては第8節で述べます。 この原理を使って分光器を作ることができます。
ふたつめの分散とは、光が屈折するとき光の色(波長)によって、ことなった方向に屈折する(屈折率が違う)ことによるものです。 三角形のプリズムを使って虹を作ることができるのはこの原理によるものです。 プリズムがなくても、水を張った洗面器に鏡を斜めに入れ、 反射された光を見ても虹が見えるでしょう。
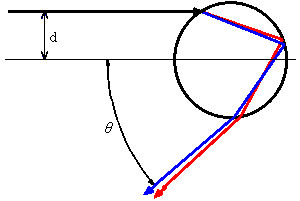 虹は光の分散によってできますが、その過程は少し複雑になります。水滴に入った光は、屈折して進み、反対側の水滴表面に当たると、
そこで反射され戻ってきます。再び、水滴表面にぶつかり抜け出してきたときには、入った方向と正反対の方向からずれています
(右図上)。光が水滴にはいるときと、水滴から出る時に屈折し、光が色によって分けられます。このときの赤色と青色
(ふつうは紫色にしますが本文主旨に従い以後青色にします)の光の経路を示しています。これで光は虹に分けられたようですが、
実際には出て行くときの角度が問題になります。
虹は光の分散によってできますが、その過程は少し複雑になります。水滴に入った光は、屈折して進み、反対側の水滴表面に当たると、
そこで反射され戻ってきます。再び、水滴表面にぶつかり抜け出してきたときには、入った方向と正反対の方向からずれています
(右図上)。光が水滴にはいるときと、水滴から出る時に屈折し、光が色によって分けられます。このときの赤色と青色
(ふつうは紫色にしますが本文主旨に従い以後青色にします)の光の経路を示しています。これで光は虹に分けられたようですが、
実際には出て行くときの角度が問題になります。図で水滴の中心から離れたところを通る光を考えます。 水滴の半径に対して中心からどれだけ離れているかを割合で表したものをd、もと来た方向からずれた角度をθとします。 dを横軸に、θを縦軸にとってグラフを書いてみると右下の図中太線のようになります。青線は青色の光、赤線は赤色の光を表しています。
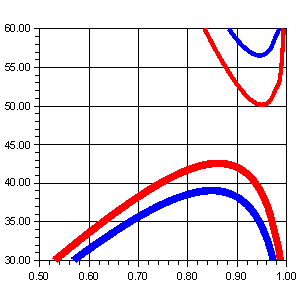 グラフから読み取れるのは、赤色では中心から82〜92%の位置に入った光は、43度の角度で出て行きます。
つまりこの角度で出てくる光がたくさんあるため明るくなります。これは、太陽に正反対側から43度の半径で円形の赤色の虹が見えることになります。
同様に青線からは、半径38度の所に青色の虹ができることを表しています。
グラフから読み取れるのは、赤色では中心から82〜92%の位置に入った光は、43度の角度で出て行きます。
つまりこの角度で出てくる光がたくさんあるため明るくなります。これは、太陽に正反対側から43度の半径で円形の赤色の虹が見えることになります。
同様に青線からは、半径38度の所に青色の虹ができることを表しています。水滴にはいった光が水滴の内側から表面にぶつかった時に、1回目は反射するのに、2回目は通り抜けて屈折するというのは変な話です。 実際は、反射するものと屈折するものには、一定の割合で別れます。そこで、2回反射して3回目に通り抜けてくるものもグラフに入れてみました。 図で、右上の方から垂れ下がってくる赤青細線です。この場合、出てくる角度θは図下方向ではなく上方向にとっています。 赤色は50度、青色は57度付近に集中する場所があることがわかります。これが主虹の外側に色の並びが逆向きにできる副虹です。
 虹の色を考える前に、色の性質について整理することにします。絵の具などで色を作るとき、色を混ぜ合わせることで別の色を作ることができます。
たとえば緑色は、青色と黄色を同量混ぜ合わせることで作り出すことができます。ところが、どう色を混ぜ合わせても作り出せない色があります。
白と赤と青と黄色です。このうち白は色を塗っていない場合と考えて除外すると、3色が残ります。この3色を色の3原色といいます。
右図上は、ふつうにいわれている色の3原色とその組合せによってできる色の見本です。
虹の色を考える前に、色の性質について整理することにします。絵の具などで色を作るとき、色を混ぜ合わせることで別の色を作ることができます。
たとえば緑色は、青色と黄色を同量混ぜ合わせることで作り出すことができます。ところが、どう色を混ぜ合わせても作り出せない色があります。
白と赤と青と黄色です。このうち白は色を塗っていない場合と考えて除外すると、3色が残ります。この3色を色の3原色といいます。
右図上は、ふつうにいわれている色の3原色とその組合せによってできる色の見本です。色を混ぜ合わせるといえば、光の色も混ぜ合わせて作ることができます。スポットライトで別々の色をあて、違った色の光にすることができます。 たとえば、青色の光と赤色の光で紫色の光ができます。光の場合も、色の時と同じように、どう混ぜ合わせても作り出すことのできない色があります。 青色と緑色と赤色と黒色です。このうち黒色の光というものはありません。ただ光が当たっていないだけです。これを除外して考えると、 どうしても作り出せない色は3色になります。これを光の3原色といいます(右図中)。
このようにしてみると、不思議なことが一つだけあります。両方の3原色で青・赤が共通なのに、緑と黄色だけが別々に入っていることです。 この疑問は、カラー写真の現像を始めたときに解決しました。カラー写真で、色の調整を行うフィルターは、シアン(C)・イエロー(Y)・ マゼンタ(M)の3色あります。最近では、カラープリンターのインクに使われている色の最小の組合せでもあります。 プリンターで考えるとわかりやすいと思います。この3色あれば、どんな色でも作り出すことができるのことになります。 シアンは水色っぽい色ですが、青といえないこともありません。 また、マゼンタは赤紫のような色ですが、 これも赤と呼べないこともありません。ようするにこの3色が赤・青・黄色の3原色だったのです。さらにこの3色は、 コンピューター画面で色の基準となっている、R(レッド=赤)・G(グリーン=緑)・B(ブルー=青)のうちの2色を等量混ぜ合わせてできる色です。 色の名前を正確にいうと、シアン・マゼンタ・イエローが色の3原色で、レッド・グリーン・ブルーが光の3原色ということになります。
正しい色の3原色を、右図下に書きました。中段の図と下段の図では色のはまっている場所が違うだけで、同じ順番に入っていることがわかります。 また、シアン・イエロー・マゼンタの位置に対して、真ん中の黒か白を挟んで反対側にレッド・グリーン・ブルーがあります。 これは、それぞれが補色(混ぜ合わせると灰色になる)の関係にあることを示しています。
どうして、色や光にはは3原色があるのでしょうか。
それは、人間の目が色を感じ取る仕組みにかくされています。目の中には、赤色を感じ取る細胞、緑色を感じ取る細胞、青色を感じ取る細胞、 明るさを感じ取る細胞の4種類があります。この中で、色に関係しているのは最後の明るさを感じ取る細胞以外の3つの細胞です。 いま、赤色の光が入ってきたとします。この光によって、赤色を感じる細胞だけが光がやってきたと感じ、赤色であると識別します。 緑、青色についても同様です。次に、赤色と緑色の光が同時にやってきたとします。このときは、赤色と緑色を感じる細胞が、 光を感じ取り、青色を感じ取る細胞は反応しません。このときは光の強さの割合によって変化しますが、橙や黄色の光がよってきたように感じます。 同じように、水色(シアン)や紫色も感じ取ることができます。逆に、純粋に赤色に反応する細胞だけが感じ取る光を、 赤色以外の色の光の組合せからは作ることができません。緑色や青色についても同様です。赤緑青が光の3原色といわれる所以です。
色の3原色について考えてみましょう。ものに色がついて見えるのは、いろいろな色の光が当たっていて、 そのうち吸収されず反射してくる光が見えるからです。たとえばシアンを考えてみます。この色が見えるのは、赤色の光を吸収し、 緑・青の光が反射され目に入ってくるからです。これに黄色を混ぜたとします。黄色は青色を吸収しますから。2色で赤・青の光を吸収し、 残った緑色の光だけが反射され目に入ってくることになります。これが、緑色を作り出すことができるできる理由です。 色の3原色とは、光の3原色のどれかを吸収してできる色なのです。だからこそ、この二つの関係は補色になるのです。
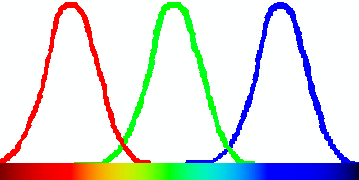 それでは、虹の色はどのようにして見えるのでしょうか。右図はその方法を表しています。
図の下に虹のように並んでいるのは、光の波長によって見える色を表しています。上にある線は赤・緑・
青に反応する細胞がどれだけ反応しているかを表し、上に上がるほど反応が強くなっている事を示しています。黄色に見える光があったとします。
この光は、赤と緑色の2種類の光が混ざっているのではなく、赤に反応する細胞と緑に反応する細胞の両方を同じだけ刺激しているので、
2種類の光が当たったと同じように感じるのです。
それでは、虹の色はどのようにして見えるのでしょうか。右図はその方法を表しています。
図の下に虹のように並んでいるのは、光の波長によって見える色を表しています。上にある線は赤・緑・
青に反応する細胞がどれだけ反応しているかを表し、上に上がるほど反応が強くなっている事を示しています。黄色に見える光があったとします。
この光は、赤と緑色の2種類の光が混ざっているのではなく、赤に反応する細胞と緑に反応する細胞の両方を同じだけ刺激しているので、
2種類の光が当たったと同じように感じるのです。それでは、紫色はどうでしょうか。緑に反応する細胞を刺激せずに、赤と青に反応する細胞を刺激することはできるでしょうか。 図を見る限り、そのような波長の光はありません。つまり橙や黄色と違って、紫色は赤・ 青2種類の波長の光が同時に入ったときにだけしか見ることができません。カラー写真も、感光剤の感度を人間の目に合わせて作っています。 だから、スペクトルを撮ったときには紫色は写らなかったのです。
結局は、虹の七色の中で、特別な色は紫色だったのです。なぜなら、紫色になる波長の光は存在しないからです。 紫色の光がない以上、紫外線(ウルトラバイオレット)というのも変ですが(藍外線になるのかな)、この点については深入りしないことにします。
≪補足(2014年6月1日 追記)≫
プリズムなどで作った虹をみると、青色よりやや紫がかった色に見えることがあります。紫なのか青なのか微妙な色合いで, 紫でないのかといわれて少し考えるような色です。微妙なので強引に青といっていました。でも完全な青でないことははっきりしています。 近くのパソコンの画像ソフトを使って近い色を作ってみたところ、RGB値で#4000FF位の値を示しました(モニタの違いによっても多少変わるようです)。 青色強度の4分の1程度の強さで赤色が混ざっていることになります。このことから、人間の目は、 短波長側で再び赤色に反応する錐体細胞の感度があがることが予想されます。肝心の所がありませんが、 ウィキペディアの錐体細胞の感度を書いた図にその様相がうかがえます。 この図を見ながら脳内で色をどう判定しているかを考えると、色の感じ方はかなり複雑になっていると思えます。
なお、RGB値#4000FFは見た感じでは、青紫と青の真ん中ぐらいに見えます。この色の色相をそのままにして、 彩度や明度をいじると日本工業規格で決められた菫色(#6D52AB)や一般的な菫色(violet;#705DA8)に近い色(値)ができます。 薄紫のような色なのですが、青色をそのまま明るくしたとします。 この場合でも水色にはならず、もっと紫味がかった感じの色になりますから、菫色は紫色と言っていいのかどうかわかりません。
虹の七色の内、紫色をバイオレットをそのまま訳して、菫色といっていた時期があったようです。 このほうが紫色というよりもよかったかもしれません(菫外線という言葉も紫外線というよりよかった?)。ただ、菫色が純色でないのは問題です。 なお、インターネットで決められているバイオレットは#EE82EEで、純色にすると#FE00FF位になります。 この色は、赤と青が等量混ざった色で、見た目は赤紫色(マゼンタ)です。かなり赤みがかった色といえます。 日本工業規格の紫(#A260BF、純色にすると#B000FF)より、もっと赤の比率が大きくなっています。 西洋のバイオレットと日本の菫は花の色が違っているためか、言葉から感じる色が違うようです。
本文中では、#4000FFは、青紫(#8000FF)と青(#0000FF)の中間なので、紫色とするより青色として取り扱っています。 青紫色でも適切だったかも知れません。この色に対して、空にできる虹には、明らかに紫色といえる色が混じっています。 紫色がないという説明では、空の虹にはあるけれども、スペクトル(プリズム)の虹には見えない紫(っぽくみえる) 色があるという意味で考えてください。
最近のデジタルカメラの中には、青より短い波長の色も再現できるものがあるようです。極端に強調されすぎて、 紫色に近い色で写るものがあるようです。少なくとも、短い波長の光は、フィルム写真では紫味がかって写ることはありません。 色がなるかないかは、肉眼より、写真によって判断したものが多数あります。
<補足の参考>
ウィンドウズソフトでの色の作り方
ウィンドウズのペイントでは、次のように操作します。メニューバーの「色」クリック→「色の編集」クリック→「色の作成」クリック→明るさ: 120(最大値の半分)→虹のような模様でマウスをクリック→出てきた印をドラッグ(一番上で)→「色|純色」の窓に色が表示されると同時に、 「赤」「緑」「青」の窓にそれぞれのRGB値が表示されます(ただし10進数)。「赤」「緑」「青」の窓に数値を入力することで色を作ることができます。
RGB値
コンピューターで色を出すとき、光の三原色である赤(red)緑(green)青(blue)の強度をそれぞれいくらにするかで表します。 強度は0〜255(65535を使うこともある)の数値で表し、16進数(先頭に16進数を表すための記号&Hをつけ0123456789ABCDEFの文字を使う、 2桁または4桁になる)に直した数値を順番に並べて使います。#4000FFは、それぞれの色の強さが最大輝度の25%(&H40/&HFF=4×16/255)、 0%、100%であることを表しています。純色は、どれか一つがFFで、もう一つが00になります。
紫色の光は存在しません。ところが、空にかかる虹や虹の写真を何度見返しても、紫色っぽいところがあるのです。 これはどうしてでしょうか。考えられることをひとつずつ検証していくことにします。
まず考えないといけないことは単なる錯覚ではないのだろうかということです。強い青の反動で、その横に紫色が見えるといことです。 一般的に反動で色が現れる場合、その補色であることが多くこの場合は黄色になり不自然だということがわかります。 錯覚によってあり得ない色が見えたりすることもありますので確認が必要です。 厳密に確かめるには、虹の拡大写真を撮り、紫の部分だけを取り出してみることで解決します。明らかに紫色に見える部分があるのです。 パソコンの画面上でフォトレタッチソフトを使って確認することができます。色の選択ツール(スポイド型をしたアイコンから入る) でカーソル(大概はスポイド型になっている)を移動させると、その場所のRBG値を読み取ることができます。 赤色から少しずつ内側にカーソルをずらしていくとR(赤)の値は小さくなりますが、紫色に見える場所で再びわずかに大きくなり、 さらに内側では小さくなります。Rの値が大きくなることは、赤色の光が増大していることを示しています。 これらのことから、紫色が見えるのは錯覚ではあり得ないことがわかります。青色の外側に赤色が混ざる理由を考える必要があります。
赤色の光を再び増大させる方法はいくつか考えられます。一つ一つを検証していきます。
一つめとして、水滴の形が球形でないことによるのではないかと考えてみます。水滴が楕円形(回転楕円体)の場合水滴中に入った光が、 その裏側で反射する場所は球形の場合と異なりますので、虹のできる角度が変わることがわかります。このような影響を及ぼすのは、 水滴を見る方向に伸びているか縮んでいる形をしている場合です。この二つの形は水滴が振動することによって、 互いに入れ替わって行きます。ところが、伸び縮みする方向は、水滴を見る方向に限らずさまざまな方向を向きますので、 虹を薄くする以外の効果はもたらさないことになります。
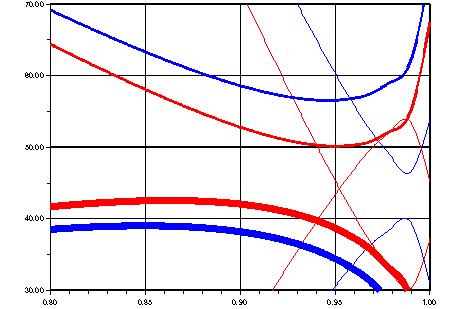 ふたつめとして、水滴内を何回も反射した光の影響があると考えてみます。水滴中を何回か反射した赤い光が、
青の外側に出てくるかどうかを考えてみます。右図は、虹のでき方の図下側を、右二目盛り分だけを横に拡大したものです。
一番太い赤線青線は一回反射した光のものです。横にだけ大きく拡大したのでほとんど横線になっています。
二番目に太い線は二回反射した光のものです。反射回数を増やしていくと、5回と6回のものが図中に入ってきます。
右側細線で下から盛り上がってきているものが5回反射したもの、上から垂れ下がっているのが6回反射したものです。
6かい反射した赤い光は、主虹の内側に入ってきます。これが、紫色にする赤い光の正体なのでしょうか。
ちょっと離れすぎているような感じもしますし、主虹より5回も余分に反射することで光そのものも弱くなっている
(80%反射するとしても30%の強さになる)上に、曲線が尖りすぎていることから集める光は少ないことになります。
おそらく6回反射してできる虹は見えない可能性が高いでしょう。5回反射の虹も主虹と副虹の間に見えないし、
3回反射・4回反射の虹(太陽から約45度離れた所に見えるはず)もはっきりしません。
6回反射の赤色虹が、紫色虹を作る赤色光の原因ではないでしょう。
ふたつめとして、水滴内を何回も反射した光の影響があると考えてみます。水滴中を何回か反射した赤い光が、
青の外側に出てくるかどうかを考えてみます。右図は、虹のでき方の図下側を、右二目盛り分だけを横に拡大したものです。
一番太い赤線青線は一回反射した光のものです。横にだけ大きく拡大したのでほとんど横線になっています。
二番目に太い線は二回反射した光のものです。反射回数を増やしていくと、5回と6回のものが図中に入ってきます。
右側細線で下から盛り上がってきているものが5回反射したもの、上から垂れ下がっているのが6回反射したものです。
6かい反射した赤い光は、主虹の内側に入ってきます。これが、紫色にする赤い光の正体なのでしょうか。
ちょっと離れすぎているような感じもしますし、主虹より5回も余分に反射することで光そのものも弱くなっている
(80%反射するとしても30%の強さになる)上に、曲線が尖りすぎていることから集める光は少ないことになります。
おそらく6回反射してできる虹は見えない可能性が高いでしょう。5回反射の虹も主虹と副虹の間に見えないし、
3回反射・4回反射の虹(太陽から約45度離れた所に見えるはず)もはっきりしません。
6回反射の赤色虹が、紫色虹を作る赤色光の原因ではないでしょう。 3番目として、空気中の水滴の分布が均質な場合を考えてみます。このとき水滴の周りで回折した光が干渉し、虹のような模様を作ることがあります。
光環がその例です。
虹のできる方向には水滴がたくさんありますからそのようなことが起こることはあり得ます。
虹の光を中心にして、回折干渉によって青色の内側に別の虹が作られ、
主虹の青と干渉虹の赤が合わさって紫に見えていると考えるのが正しいでしょう。
実際に内側にたくさんの虹を持つ虹の撮影に成功しました(右写真)。このような虹は過剰虹と呼ばれています。
次節で、過剰虹のできる仕組みについて、詳しく見ていくことにしていきます。
3番目として、空気中の水滴の分布が均質な場合を考えてみます。このとき水滴の周りで回折した光が干渉し、虹のような模様を作ることがあります。
光環がその例です。
虹のできる方向には水滴がたくさんありますからそのようなことが起こることはあり得ます。
虹の光を中心にして、回折干渉によって青色の内側に別の虹が作られ、
主虹の青と干渉虹の赤が合わさって紫に見えていると考えるのが正しいでしょう。
実際に内側にたくさんの虹を持つ虹の撮影に成功しました(右写真)。このような虹は過剰虹と呼ばれています。
次節で、過剰虹のできる仕組みについて、詳しく見ていくことにしていきます。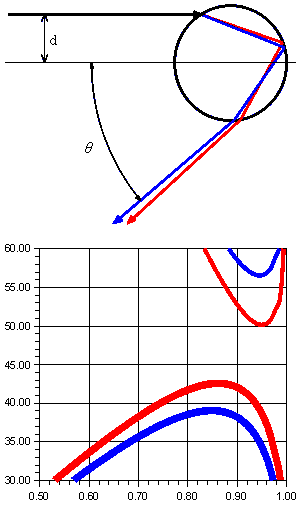 ここでは、過剰虹ができる仕組みを表計算ソフトを使って考えることにします。その前に、どのようなことが考えられるか、原因を探ります。
何度も虹模様が繰り返されることから、光の干渉が関係しているといえます。雨が降っている空の中で、干渉を起こる場合は、二通り考えられます。
一つは、雨滴の上端と下端を通った光が起こす干渉です。光環はこの方法でできる虹の例です。光環型と呼ぶことにします。
ここでは、過剰虹ができる仕組みを表計算ソフトを使って考えることにします。その前に、どのようなことが考えられるか、原因を探ります。
何度も虹模様が繰り返されることから、光の干渉が関係しているといえます。雨が降っている空の中で、干渉を起こる場合は、二通り考えられます。
一つは、雨滴の上端と下端を通った光が起こす干渉です。光環はこの方法でできる虹の例です。光環型と呼ぶことにします。もう一つはちょっと複雑です。説明のため2節の図を再度載せます。たとえば、雨滴の中を通り抜け、来た方向から40度の角度で出て行く赤い光を考えます。 この角度で出て行く光が雨滴にはいる位置は、0.74と0.94の2カ所あります(赤線が40の横線と交わる位置)。この二つは道筋が違うので、その長さも異なります。 経路の長さが異なる二つの光は干渉を起こします。この方法をここでは経路差型と呼ぶことにします。
いずれの場合も粒径によって虹模様のでき方は異なりますので、粒径が変わっても自動で再計算してくれるようにします。 表計算ソフトによって少し操作は異なりますが、説明はOpen Office Calcで行います。Excelでは関数内の「;」を「,」に書き換えることで使えます。
計算しないから、作り方の説明はいらないという方は結論まで読み飛ばしてください。
<光環型の場合>
まず基本データを入力します。表のように入れてください。
| A | B | C | D | E | F | G | |
| 1 | 雨粒直径→ | 0.04 | red | yellow | green | cian | blue |
| 2 | 角度↓ | 0.00078 | 0.00068 | 0.00058 | 0.00048 | 0.00038 | |
| 3 | 45.00 | ||||||
| 4 | 44.90 |
B1セルの値は、雨粒の直径を入力する欄です。あとで適当に数値を入れてください。その隣に並ぶ英語表記の色名は別に日本語でもかまいません。 シアン・青については、従来の虹色の青・藍でも特に問題はありません。色名のその下の数値は、光の波長(mm)です。こちらの方が意味を持っています。 次に、A3とA4のセルを選択し下に引っ張っていって連続データを作ります。96行まで引っ張り35.7ができるあたりまででいいでしょう。 なお作成例では、この列の数値は小数第2位まで表示するようにしています。
その次は、虹の各色ができるところに目印をつけます。赤は42.2度のところにできますから、51行にある42.2の隣のセル(B51)を赤く塗ります。 (セルで右クリック→セルの書式設定→背景タブ→色を選ぶ)
| A | B | |
| 51 | 42.00 |
同様に、B列の36行(41.70)、41行(41.20)、46行(40.70)、51行(40.20)をそれぞれ黄、緑、シアン、青で塗ります。 次に計算式を入力します。C3のセルは次のようになります
方法は、C3セルを選び、メニューバーの書式→条件付き書式設定で、 条件1セルの値が、次の間でない、0.25と0.75
セルスタイルの欄は、新しいスタイルから 名前=赤(これは適当でよい) 背景タブ→赤色を選択 OKをクリック
エクセルでは、ホーム→条件付書式設定→新しい書式ルール→指定の値だけを含むセルだけを書式設定→次の値の間以外:0.25と0.75、書式→塗りつぶしタブ:赤、全てOK
同様にD3からG3のセルは順番に=MOD($B$1*SIN(($A3-$A$41)*PI()/180)/E$2;1)
=MOD($B$1*SIN(($A3-$A$46)*PI()/180)/F$2;1)
=MOD($B$1*SIN(($A3-$A$51)*PI()/180)/F$2;1)です
最後に、C3からG3のセルを選び下に引っ張っていってできあがりです。
ここで、「引っ張る」というのは、セルを選択したあと、選択範囲を示す枠の右下にマウスを持って行くとカーソルの形が「+」になります。
この状態のままマウスをドラッグすると選択範囲が広くなり元の選択範囲にあったデータなどがコピーされる状態を言います。
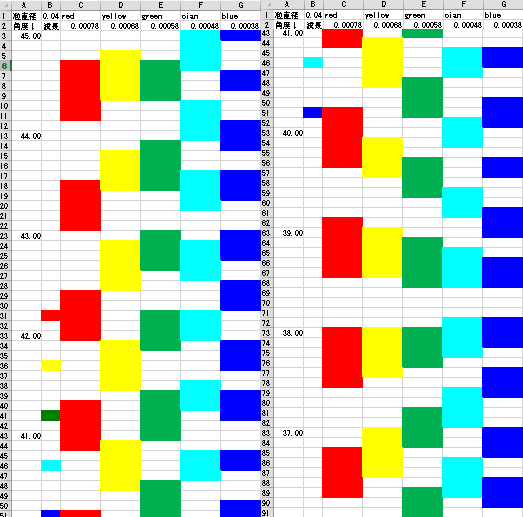 できあがった結果の例を示します
(計算結果の数値は見えないようにしています)。縦に長くなるので、虹の外側と内側に分けて並べています。
B1セルの値をいろいろ変えてみて、どうなるかを試してみてください。
できあがった結果の例を示します
(計算結果の数値は見えないようにしています)。縦に長くなるので、虹の外側と内側に分けて並べています。
B1セルの値をいろいろ変えてみて、どうなるかを試してみてください。赤から青の色がついたところが下にずれながら並んでいると虹になって見えます。 計算の結果からわかることは、粒の直径が雨粒(1mm程度)に比べて小さいこと、内側にはせいぜいできても2回くらいの繰り返しであること、 赤から緑くらいの色の範囲で外側にもできる場合があること(青は次数:中心の位置からの何回目かが大きいので弱い)などにより、原因とは考えにくそうです。 霧のようなものをまとうような雨ならこの条件のものはできないとはいいきれません。
<経路差型の場合>
経路差型の計算をさせようとしたときやっかいな問題が一つ生じます。それは、出て行く角度が決められたとき、 その光はどこで入射したものかを求めないといけないということです。おまけにその解は二つあります。 したがって、単純に計算式で求められるようなものではなくなってきます。そこで技を使うことにします。入射位置に対して出て行く角度の一覧表を作っておき、 その表を参照して、この角度で出て行く光の入射位置を探す方法です。三角関数の値が0.3になる角度を三角関数表から求めるのと同じ方法です。
一覧表を作ります
| A | B | C | D | E | F | G | |
| 1 | 入 | 1.330 | 1.333 | 1.336 | 1.340 | 1.345 | |
| 2 | 35.00 | 35.00 | |||||
| 3 | 35.01 | 35.01 |
1行目は、光の屈折率です。左から順に、赤・黄・緑・シアン・青と想定します。
A列に入るのは、水滴の表面に直角に引いた線に対して光が何度の角度で入ってくるかを示します。この角度は、水滴の中心から見たとき、 光の入ってきた位置が、光がやってきた方向に対して何度離れているかという角度と同じです。
計算は、0.01度おきにすることにします。 小さいほど精度が上がりますが、これ以下にしても、計算結果に大きな違いは出てきません。最大は90度ですので、90.00まで作ります。 一応小数第2位まで表示させてください。表は膨大になりますが、最近のパソコンは処理が速いので、計算はあっという間に終わります。
G列は、あとで使う関数の処理に必要です。A列をコピーするか「=A2」のように入力してください。
次に出て行く角度を求める計算式を入力します。セルB2には
| A | B | C | |
| 5505 | 最大角度 | ||
| 5506 | 入射角 | ||
| 5507 | 番地 |
入力する計算式です。B5505からB5507までは次の式を入れます。
B5506 =VLOOKUP(B5505;B2:$G5502;6;0)
B5507 =ADDRESS((B5506-34.98)*100;2)
5507行の関数にある、減数の34.98は表全体に入射角が記入されているとしたとき、0行目(あると仮定してください)に入る入射角です。 乗数の100は入射角の刻みの大きさ00.1の逆数です。この式で、何をしているかというと、求めたい入射角の入っている行は、上から何番目になるかを角度から計算しています。 第2引数は、B列とかC列とか書かせるためのものです。
| A | B | C | |
| 5505 | 最大角度 | 42.516381 | 42.078107 |
| 5506 | 入射角 | 59.58 | 59.41 |
| 5507 | 番地 | $B$2460 | $D$2426 |
| I | J | K | L | M | N | |
| 1 | \波長 角度\ | 赤 | 黄 | 緑 | シアン | 青 |
| 2 | 42.5 | |||||
| 3 | 42.4 |
角度の一番大きなものは赤の42.516と求められましたので、それより大きな角度は意味がありません。 それより小さな42.5から0.1刻みで計算させることにします。37.0位までで十分なのでそこまで(57行)引っ張ってください。
| 0 | P | Q | R | S | T | |
| 1 | | 赤 | 黄 | 緑 | シアン | 青 |
| 2 | ||||||
| 3 |
P2に入る計算式です。
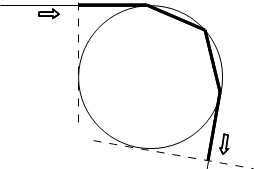 次は、ここまでの計算でやっと求められた入射角に対して、雨粒の半径を1としたとき、光の経路の長さがいくらになるかを求めることにします。
どこからどこまでかが大事になりますが、光が雨粒の表面を真横に見る(光路に直角に引いた線が雨粒の接線となる)点から同じようになる点までとします
(右図太線区間)。また、雨滴内は、屈折率をかけることで、所要時間に関係する長さに変換しておきます。
次は、ここまでの計算でやっと求められた入射角に対して、雨粒の半径を1としたとき、光の経路の長さがいくらになるかを求めることにします。
どこからどこまでかが大事になりますが、光が雨粒の表面を真横に見る(光路に直角に引いた線が雨粒の接線となる)点から同じようになる点までとします
(右図太線区間)。また、雨滴内は、屈折率をかけることで、所要時間に関係する長さに変換しておきます。表を作ります。
| V | W | X | Y | Z | |
| 1 | 1.330 | 1.333 | 1.336 | 1.340 | 1.345 |
| 2 | |||||
| 3 |
| AB | AC | AD | AE | AF | |
| 1 | 1.330 | 1.333 | 1.336 | 1.340 | 1.345 |
| 2 | |||||
| 3 |
1行目は、光の屈折率です。2回繰り返されているのは、最大値になるまでの経路と最大値になってからの経路の2通りを計算しないといけないからです。 セルV2に入る計算式です。
厳密にするためには次のように求めていくことが必要です。まず、ある入射角で入った光の強さは、その角度に対応する出て行く角度と、 それより決まった角度(たとえば0.1度)離れた角度で入った光が出て行く角度との差の逆数に入射角のサインをかけたものになります。 また、二つの波の合成は次の式で求めます。
Asin(θ)+Bsin(θ+α)=Csin(θ+β)
ここで、sinとθは波ですよというおまじないみたいな文字、ABはそれぞれの波の強さ。 αは波のずれ(2π×経路差÷波長)、βは元の波とのずれ(今回の計算では意味がないので詳しいことは省略します)です。
Cが合成された波の強さで、C2=A2+B2+2×A×B×cosα で求めます。A=Bなら単純に |2Acos(α/2)| になります。
| AI | AJ | AK | AL | AM | AN | |
| 1 | 0.00078 | 0.00068 | 0.00058 |
0.00048 | 0.00038 | 雨粒半径 |
| 2 | 0.200 | |||||
| 3 |
1行に並んでいる数字は、光の波長です。AN2に雨粒の半径を入力することにします。光環型に合わせて直径の方がよかったかも知れませんが、これでいきます。 とりあえず0.2を入力します。AI2に入る計算式です。
 0.5を引いてから絶対値を取っているのは、波が強めあうのが0と1に近いときであるのを、0.5近辺にするためです。
入力が終わったら、横にAM列まで引っ張ってください。条件付き書式設定もしておいてください。0.25より大きなものが強めあっているとして色がつくようにします。
結果が「--」でないセルだけ設定するようにした方がいいかもしれません。終われば、AI1からAM1を下へ(57行まで)引っ張って完成です。
表がいっぱいでわかりずらいので、 I列とAI〜AN列をのぞいて「表示しない」設定にするといいでしょう。
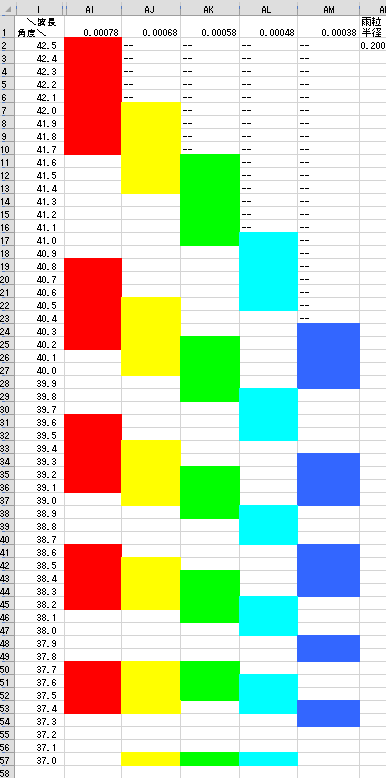
結果の一例を右に示します(計算結果の数値は見えないようにしています)。
0.5を引いてから絶対値を取っているのは、波が強めあうのが0と1に近いときであるのを、0.5近辺にするためです。
入力が終わったら、横にAM列まで引っ張ってください。条件付き書式設定もしておいてください。0.25より大きなものが強めあっているとして色がつくようにします。
結果が「--」でないセルだけ設定するようにした方がいいかもしれません。終われば、AI1からAM1を下へ(57行まで)引っ張って完成です。
表がいっぱいでわかりずらいので、 I列とAI〜AN列をのぞいて「表示しない」設定にするといいでしょう。
結果の一例を右に示します(計算結果の数値は見えないようにしています)。セルAN2に適当な数字を入れて、にじのでき方がどのように変わるかを見てください。
半径が0.2mm前後で虹模様が繰かえされてできます。虹が繰りかえされる幅も写真のものと似ているようです。
<結論>
光環型の場合、計算結果から考えると、雨に霧粒が混ざっている場合できないことはないが、 霧粒の影響で透過度は下がり、それほどの回数は繰り返さないし、虹の外側にもできることがある。特に3番目のものは、観測された例を聞かないので、 このタイプのものはないのかも知れない。
経路差型の場合(結果は右上にでています)はきれいな虹の繰り返しを作ることができた。水滴の直径も、雨粒の大きさに該当する。 以上のことから、過剰虹の主原因と考えられる。
いずれの場合も、水滴の大きさが変わると、虹模様のできるパターンが異なるので、水滴の大きさがそろっていることが、過剰虹のできる条件としていえる。
※表をダウンロードできます↓(ZIP形式に圧縮しています)
open office 形式(topic09-ods;544kb)
エクセル97形式(互換性のため;topic09-xls:478kb)
 空の色が青いわけはさまざまな解説書に書かれています。簡単に述べると次のようになります。太陽光は大気に含まれる微粒子によって散乱を受けます。
散乱される度合いは、波長が短いほど大きくなりますので、元の光より青みがかった光が大気からやってきますので、大気が青く光ります。
また、大気の層を長距離にわたって通り抜けてきた光は、波長の短い成分が取り除かれ赤っぽくなります。これが夕焼けです。
右写真は、飛行機から撮った夕焼けです。地上で見てもこのように見えます(これほどすぐには暗くならない)。下の方の赤っぽいのが、大気を通り抜けた光、
上の方の青っぽいのが散乱した光です。見ていると虹を逆さまにしたようにも見えませんか。
空の色が青いわけはさまざまな解説書に書かれています。簡単に述べると次のようになります。太陽光は大気に含まれる微粒子によって散乱を受けます。
散乱される度合いは、波長が短いほど大きくなりますので、元の光より青みがかった光が大気からやってきますので、大気が青く光ります。
また、大気の層を長距離にわたって通り抜けてきた光は、波長の短い成分が取り除かれ赤っぽくなります。これが夕焼けです。
右写真は、飛行機から撮った夕焼けです。地上で見てもこのように見えます(これほどすぐには暗くならない)。下の方の赤っぽいのが、大気を通り抜けた光、
上の方の青っぽいのが散乱した光です。見ていると虹を逆さまにしたようにも見えませんか。ところで、今までのこの文を呼んだ人は、この解説を読むと一つの疑問が湧いてきませんか(もっとも最近まで気がつかなかったのですが)。何かというと、 波長が短くなるのなら、なぜ紫ではなく青色なのでしょうか。大気からの散乱光には大量の紫外線が含まれていますので、 紫色の光がたくさん含まれていてもおかしくないはずです。それなら空の色は紫になります。
考え方は、二つあります。一つ目は、散乱される光に含まれる緑色やそれより波長の長い光と混ざり合って消されるとする考え方です。 夕焼けの色から考えてみると、黄色より波長の長い光はほとんど散乱されないと見ていいでしょう。緑色もそんなに散乱されているとは思えません。 これだと、もっと紫っぽくなってもいいようです。
二つ目の考え方です。紫色になる波長の光はないとすればどうでしょうか。散乱され目で見える光の中で最も波長の短い光は青色です。 青色の光がもっともたくさん散乱されるので空は青く見えることになります。 このように紫色の光はない事は、空の色からも説明できます。
同様なことが、恒星の温度とスペクトル型の関係にも表れています。高温な恒星から順番に青(O型星)、青白(B型星)、白(A型星)、 と順番に変わっていきます。A型星で、全ての波長の光が均等に放射されます。それより高温の星では波長の短い光の成分が多くなります。 この時多い光の主体は、目で見える最短の波長の光となります。従って、恒星の色は、紫や薄紫といった色になるはずです。 実際に青系統の色になっているのは、紫色になる波長の光が存在しないからといえます。
夕焼け空が、虹のようになっていると書きましたが、それ以外でも虹のように見える現象があります。雲や大気に関係のあるものについて見ていくことにします。 氷晶によってできる虹については別途解説していますのでそちらをご覧ください。
<0次の虹>
 虹は、水滴内に入った光が水滴表面で反射することによってできます。従って、様々な種類の虹ができますが、これを光が反射した回数で呼ぶことがあります。
1回反射したものを「1次の虹」、2回なら……、というように区別します。主虹は1次、副虹は2次になります。3次・4次は、ほとんど目にすることはありません。
それでも、見たという記録はあります。5次以上を目にすることは、おそらく無理でしょう。
虹は、水滴内に入った光が水滴表面で反射することによってできます。従って、様々な種類の虹ができますが、これを光が反射した回数で呼ぶことがあります。
1回反射したものを「1次の虹」、2回なら……、というように区別します。主虹は1次、副虹は2次になります。3次・4次は、ほとんど目にすることはありません。
それでも、見たという記録はあります。5次以上を目にすることは、おそらく無理でしょう。 それでは、0回反射した場合はどうでしょうか。0回ということは、一度も反射しないことです。
水滴の中に入った光が、反射せずにそのまま突き抜けた事を意味します。このようなものがあれば、「0次の虹」という呼び方ができます。
葉っぱや物干し竿に付いた水滴を、太陽を背にしておいてみると、虹色に光ってみることがあります(右写真)。
何となく、虹色のものが空に見えそうです。完全に球形のものを通り抜けた光がどうなるかを調べてみると、様々な方向にむらなく出ていくことがわかります。
虹色に見えたのは、水滴のがいびつな形になっていたためです。
それでは、0回反射した場合はどうでしょうか。0回ということは、一度も反射しないことです。
水滴の中に入った光が、反射せずにそのまま突き抜けた事を意味します。このようなものがあれば、「0次の虹」という呼び方ができます。
葉っぱや物干し竿に付いた水滴を、太陽を背にしておいてみると、虹色に光ってみることがあります(右写真)。
何となく、虹色のものが空に見えそうです。完全に球形のものを通り抜けた光がどうなるかを調べてみると、様々な方向にむらなく出ていくことがわかります。
虹色に見えたのは、水滴のがいびつな形になっていたためです。水滴内を通り抜けた光を見ることはできます。太陽との間で雨が降っている場合、雨が明るく光ります(左写真)。これが0次の虹になるのでしょう。 主虹の内側は少し明るく光っています。この部分はふつう虹とはいいません。それなら、写真は虹ではないでしょう。 丸く輪になった部分全体を指して虹というのなら、写真のものは0次の虹といえるでしょう。
<グリーンフラッシュ(ブルーフラッシュ)>
 地球の大気は、地表近くほど濃くなっています。空気の濃度が大きくなると光の進行速度は遅くなります。光の速度で見ると地球の大気は、
地表付近ほど遅くなる構造になっています。このような場合、地表の2点間を結ぶ光は、わずかですが、伝わる速度の速い上空を通るようになります。
地球の大気は、地表近くほど濃くなっています。空気の濃度が大きくなると光の進行速度は遅くなります。光の速度で見ると地球の大気は、
地表付近ほど遅くなる構造になっています。このような場合、地表の2点間を結ぶ光は、わずかですが、伝わる速度の速い上空を通るようになります。
 光の経路が、下の方向に曲がっているといってもいいでしょう。これは、マントルを通る地震波が、より深いところを通っていくのと同じ原理です。
光の経路が、下の方向に曲がっているといってもいいでしょう。これは、マントルを通る地震波が、より深いところを通っていくのと同じ原理です。 今地平線より、わずかに沈んだ星があったとします。この星から来た光は、地面の方に曲げられます。
その結果、観測者へはより高い角度から来たように見えるようになります。右上図で、下の黒丸が、実際の星の方向、上の黒丸が星の見える方向です。
このように、地平線近く、あるいは地平線下の星が持ち上げられたように見える現象を大気差といいます。
地平線下のものも見えるようにしないといけないので、見えているものは縦方向に縮んだようになります。
日の出・日の入りの太陽がつぶれたように見えるのはこのためです(右写真)。
今地平線より、わずかに沈んだ星があったとします。この星から来た光は、地面の方に曲げられます。
その結果、観測者へはより高い角度から来たように見えるようになります。右上図で、下の黒丸が、実際の星の方向、上の黒丸が星の見える方向です。
このように、地平線近く、あるいは地平線下の星が持ち上げられたように見える現象を大気差といいます。
地平線下のものも見えるようにしないといけないので、見えているものは縦方向に縮んだようになります。
日の出・日の入りの太陽がつぶれたように見えるのはこのためです(右写真)。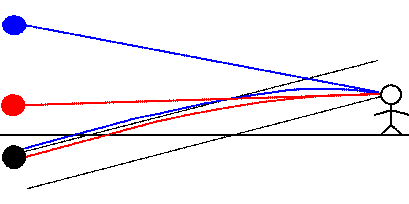 光の経路が曲がるのは、光が屈折するからです。屈折するときには、光は分散され、虹色に分かれます。この時波長の短い光ほど大きく曲がります。
曲がりが大きくなれば、その分だけ高くにあるように見えます(右図3枚目)。その差はわずかなので、天体の上端に青い色、下端に赤い色がついたように見えます。
色のずれは、高度が低くなるほど大きくなります。右下写真は、高度が低くなったために、実際に虹のようなものができている金星です。
光の経路が曲がるのは、光が屈折するからです。屈折するときには、光は分散され、虹色に分かれます。この時波長の短い光ほど大きく曲がります。
曲がりが大きくなれば、その分だけ高くにあるように見えます(右図3枚目)。その差はわずかなので、天体の上端に青い色、下端に赤い色がついたように見えます。
色のずれは、高度が低くなるほど大きくなります。右下写真は、高度が低くなったために、実際に虹のようなものができている金星です。 このように上端が青くなった天体が地平線(水平線)下に、沈もうとしている時を考えます。
完全に見えなくなる直前は、上端の青い色の部分だけが見られることになります。金星だと光が弱くて見えないかも知れません。
太陽ならどうでしょう。見えそうな感じがしますが、別の問題が起こってきます。高度が低くなるにつれ、光が大気の層を通り抜ける長さが長くなります。
大気の濃い部分もたくさん通らないといけません。そうなると、大気に含まれているちりなどにぶつかって通り抜けにくくなります。散乱といいます。
波長が短い光ほどその影響を大きく受けます。赤い光はあまり影響を受けませんので、大気の層を通り抜けてきます。朝日や夕日が赤くなるのはこのためです。
このように上端が青くなった天体が地平線(水平線)下に、沈もうとしている時を考えます。
完全に見えなくなる直前は、上端の青い色の部分だけが見られることになります。金星だと光が弱くて見えないかも知れません。
太陽ならどうでしょう。見えそうな感じがしますが、別の問題が起こってきます。高度が低くなるにつれ、光が大気の層を通り抜ける長さが長くなります。
大気の濃い部分もたくさん通らないといけません。そうなると、大気に含まれているちりなどにぶつかって通り抜けにくくなります。散乱といいます。
波長が短い光ほどその影響を大きく受けます。赤い光はあまり影響を受けませんので、大気の層を通り抜けてきます。朝日や夕日が赤くなるのはこのためです。太陽の上端は青くなるのですが、散乱の影響を受けなくなってしまい見えなくなります。 そのため、太陽が沈んで見えなくなる直前に、一瞬だけ青く光るということはありません。緑の光でも同じことがいえます。太陽は、赤いまま沈んでいきます。 滅多にありませんが、何かの理由で、大気中のちりが非常に少なかったらどうでしょう。緑色の光は通り抜けてくるかも知れません。 そうなると、太陽が沈んで見えなくなる直前に一瞬だけ緑色に光るということが起こります。これがグリーンフラッシュです。 この時の空は、太陽光が赤色の光以外にも緑色までの光を含んでいるのでそれほど赤くなっていないでしょう。 太陽も赤くならず、明るいまま沈んでいくでしょう。もっと可能性は低いのですが、青色の光も通り抜けてくることだってあります。 その時は、青く光るブルーフラッシュになります。最初の写真はブルーフラッシュになります。
太陽を隠すものは、水平線や地平線でなくてもかまいません。雲や建物、山の端、人工的な障害物でも、グリーンフラッシュやブルーフラッシュはできるでしょう。 ある程度以上高度が低くないとできません。実際に観察された例を見ると、蜃気楼によって太陽の上端が浮き上がって見えた時が多いようです。 このような条件が加わると、色がついて光って見える部分が大きくなるので見やすくなりますが、 できる条件はさらに厳しくなり、その分見る機会は少なくなります。
<光環>

 太陽や月の前を薄雲が被さると、周りに丸く虹ができます。これが光環です。虹は、2重か3重になっていることもあります。
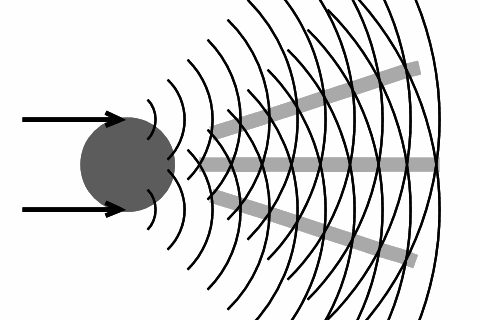
太陽や月の前を薄雲が被さると、周りに丸く虹ができます。これが光環です。虹は、2重か3重になっていることもあります。光環は、水滴の両端をかすめてきた光が干渉し合ってできます。右図で、円形の線が波の山だとすると、灰色に塗った方向に進む光が強くなります。 この方向は、光の波長が短いほど狭くなります。色によって順番に角度が変わるために虹のように見えます。
写真では、真っ赤な夕日を撮っていますので、虹の黄色から青色の部分は大気に散乱されていて、はっきりと見えていません。
<ブロッケンの虹>
 太陽を背にして霧や雲を見ると、太陽の正反対の位置を中心にして虹のようなものが見えます。この虹も2−3重になっています。
写真には薄ぼんやりと写っています。太陽の正反対側は、そこにある水滴の表面で真っ直ぐ反射してきた光が目に届くため、非常に明るくなります。
この光を中心にして、光環ができるのと同じ原理で虹模様ができます。これがブロッケンの虹です。
飛行機で飛んでいて、飛行機の影が雲に落ちているときには、この虹ができていることが多いようです。
太陽を背にして霧や雲を見ると、太陽の正反対の位置を中心にして虹のようなものが見えます。この虹も2−3重になっています。
写真には薄ぼんやりと写っています。太陽の正反対側は、そこにある水滴の表面で真っ直ぐ反射してきた光が目に届くため、非常に明るくなります。
この光を中心にして、光環ができるのと同じ原理で虹模様ができます。これがブロッケンの虹です。
飛行機で飛んでいて、飛行機の影が雲に落ちているときには、この虹ができていることが多いようです。太陽と正反対側は、実際には観測者の影ができています。これはぼやっとしていて、そこに人間の形をしたものがいるように見えます。 これは、ブロッケンの妖怪と呼ばれています。 写真にも中心に確認することができます。
<彩雲>

 雲が色づいて見える現象です。薄めの絹層雲に見られることが多いようです。太陽に近い方がよくできるようです。
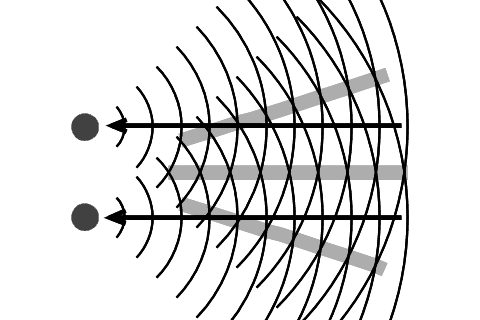
雲が色づいて見える現象です。薄めの絹層雲に見られることが多いようです。太陽に近い方がよくできるようです。2つの水滴で反射した光が、その進んで行く方向によって強めあったり弱めあったりする性質があるのでできるといわれています(右図)。 水滴の間を通り抜けた光でも同じことが起こります。この場合、水滴が均等に配置していることが条件になります。 この方法では、 雲の濃いところと薄いところで、色が違うことは説明がつきますが、 太陽との位置関係で、できやすかったりできにくかったりすることは説明できません。
<道標(top)>