流れの速い河原では、小さな砂粒は流され、大きめの石ころだけがたまっています。流速と、たまる石の粒径となにか関係がありそうです。
そのしくみについて考えていきます。
1.流速と粒径
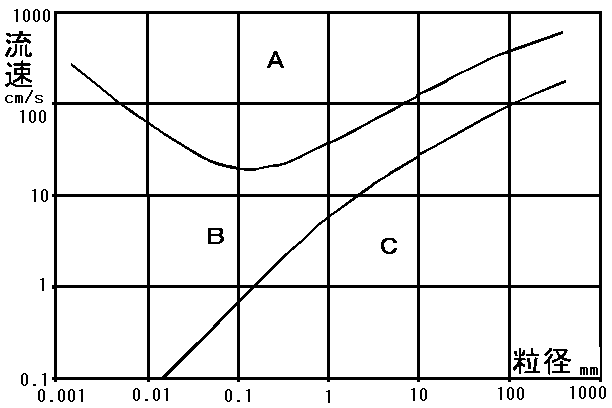
地学の教科書には、河川の流域で侵食・運搬・堆積がどのような場合に起こるかを示すために右のような図が載せられています。 ユルストローム図と呼ばれる図です。
図中Cの領域が堆積、Bの領域が運搬、Aの領域が侵食(ていねいな教科書では侵食と運搬)が起こる領域とかかれています。
もう少し詳しく見ていきます。グラフの横軸は粒径(粒子の直径)、縦軸は流速(川の流れの速さ)を表しています。 例えば、直径1mmの粒子(砂粒)があったとします。この粒子が流速1cm/sの流れの中にあるとどうなるでしょうか。 粒径1mmと流速1cm/sの位置は、Cの領域にあります。 ここは堆積の領域にあるので、この粒は堆積することになります。
流速が100cm/sになると、Aの領域に入ってきます。ここは侵食の領域ですので、この流れの中では侵食されることなります。 流速が10cm/sでは、運搬されることになります。この図からは、粒子が運ばれていくのか、運ばれてきたものが堆積するのかを読み取ることができます。
この方法を逆に使ってみることにします。洪水があって治まった後に、川底に10cm(100mm)の石がたまっていたとします。 この大きさの粒子が運ばれるのは、BとCとの境界線より上です。粒径10cmの縦線を上にたどっていって、BCの境界線と交わるところの流速は100cm/sです。 このことから、洪水時の流速はこれよりも速かったことが読み取られます。
なお、図の縦軸・横軸とも目盛りのはばが10倍(別に何倍でもよいが)になる毎に等間隔だけずれていくというつけかたになっています。 このような形の目盛りがついたグラフを両対数グラフと言います。 非常に大きな数値と小さな数値が混ざっているときに便利なグラフです。
※侵食の「しん」の字は「浸」をあてることがあります。おもに水が関わっていますから、「さんずい」の方が適切なように思えます。 人が関わらないので「にんべん」を使うのは違和感がありますが、慣例に従って「侵食」を用いることにします。 「しょく」についても「蝕(むしばむ)」が正しい文字です。
なお、このサイト内の他のページでは、習慣で「浸食」を使っているところもあります。
2.ユルストローム図の実際の意味
この図がどういう意味を持っているのかもう少し詳しく見ていくことにします。
いま、川底に砂粒が一つあるとします。この上を川の水が流れると砂粒を押す力が働きます。ところが、砂粒と川底との間に摩擦力が働きますので、 砂粒は簡単に動きません。水流が早くなって、砂粒を押す力が大きくなり、砂粒の最大摩擦力より大きくなったときに砂粒が動き出します。 この時の流速を仮に「初動速度」と呼ぶことにします。
今度は、同じ大きさの砂粒が流されてきたとします。当然、形や密度は同じものとします。この場合も、川の流れが押す力よりも摩擦力の方が大きければ、 砂粒の動いている速さはだんだん遅くなって最後には止まってしまいます。川の流れがある速度より小さくなると、砂粒が止まることになります。 砂粒がいっぱいやってくれば、この速度以下では堆積が起こるということで、これも仮に「堆積速度」と呼ぶことにします。
初動速度と堆積速度を比べてみます。摩擦力は動き出すときが最大になりますから、その分だけ動かすためには大きな力が必要になります。 したがって、堆積速度より初動速度が大きくなります。横軸に粒径、縦軸に流速をとったグラフに表してみると、初動速度の方が上になります。 いろいろな粒径で、初動速度と堆積速度を表す点が取れます。これを結ぶと初動速度、堆積速度を表す線が引けます。 初動速度を表す線は「初動曲線」、堆積速度を表す線を「堆積曲線」と呼ぶことにします。当然、初動曲線は堆積曲線より上に引かれます。
今度は、それぞれの領域が何を示しているかを考えてみます。図を再提示します。
 まず、Aの領域です。いま流速100cm/sの流れの水路で、粒径1mmの砂粒があったとします。
川底に止まっていたとしても、この領域に入る流速なら流されていきます。結局、この大きさの粒子は全てなくなってしまいます。
粒子が全てなくなるまでは運び去られます。言いかえれば、侵食されるといえます。しかし、流れは過去からずっとあったはずです。
とすると、流される粒子はとうの昔に運び去られ、なくなってしまっていると考えた方が妥当です。
つまり、侵食されるべき粒子はないので、侵食は起こらないことになります。
結局、Aの領域は侵食の領域ではないといえます。もっとも砂粒は流され続けていますから、運搬の領域であることはまちがいありません。
まず、Aの領域です。いま流速100cm/sの流れの水路で、粒径1mmの砂粒があったとします。
川底に止まっていたとしても、この領域に入る流速なら流されていきます。結局、この大きさの粒子は全てなくなってしまいます。
粒子が全てなくなるまでは運び去られます。言いかえれば、侵食されるといえます。しかし、流れは過去からずっとあったはずです。
とすると、流される粒子はとうの昔に運び去られ、なくなってしまっていると考えた方が妥当です。
つまり、侵食されるべき粒子はないので、侵食は起こらないことになります。
結局、Aの領域は侵食の領域ではないといえます。もっとも砂粒は流され続けていますから、運搬の領域であることはまちがいありません。
同様にBの領域を考えます。止まっていた粒はABの境界を越える速さではないので、動き出すことはできません。 止まったままです。逆に動いている粒は、BCの境界線を下回りませんので、止まらず動いたままです。 つまり、この領域には、同じ大きさの粒でも動いているものと止まっているものとがあることになります。
最後にCの領域です。動いていたものも止まります。堆積していくように見えますが、この流速では粒子を運ぶことはできません。 定常的な流れがあったとすると、粒子はとっくの昔に止まってしまっていて、運ばれてくることはありません。 したがって、たまるものがやってこない以上堆積は起こりえません。 この領域は、堆積の起こる場所ではなく、該当するすべての粒子が動かない領域になります。
まとめてみます。ユルストローム図の、ABCの各領域は、侵食・運搬・堆積ではなく次の状態を表していることになります。
Aの領域−−該当する全ての粒子は動いている
Bの領域−−該当する粒子は、動いているものと止まっているものがある
Cの領域−−該当する全ての粒子は止まっている
図の中で大きな意味を持っているのは、それぞれの境界線で、
ABの境界線−−止まっていた粒子が動き出す境界(初動曲線)
BCの境界線−−動いていた粒子が止まり出す境界(堆積曲線)
を表しています。
3.侵食・堆積の起こる場所
ここまでの説明では、侵食・運搬・堆積の起こる場所が図に記入されていない様に思えます。 工夫すると堆積や侵食の起こる場所も読み取ることができます。各境界線の説明を見直してみることにします。
堆積の起こる場所を考えてみます。動いていた粒子が止まるということは、堆積が起こった事を示しています。 BCの境界線はまさにそのような場所です。この線より上では、動いている粒子があります。逆に下では全ての粒子が止まっています。 この線を上から下方向に横断するように流速が変化したときに動いている粒子が止まり、その粒子が堆積します。 簡単に言えば、BC線(堆積曲線)をまたいで流速が遅くなるときに堆積が起こることになります。 1mmの粒子は流速が約6cm/sを切るようになったときに堆積します。
同様に、侵食の起こる場所はABの境界線(初動曲線)をまたいで流速が速くなるところになります。 1mmの粒子は流速が約30cm/sを越えるようになったときに運び去られ(=侵食し)始めます。
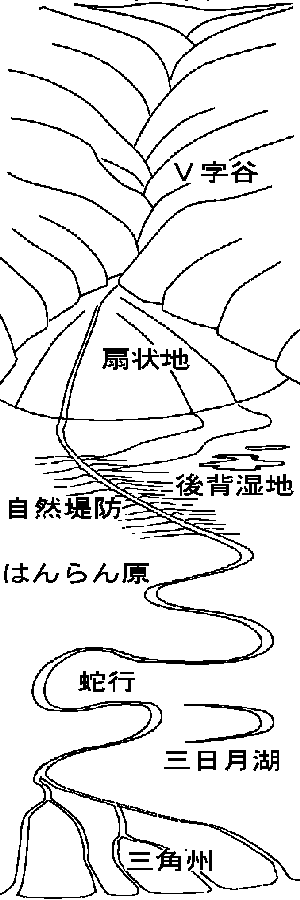 3A 河川での浸食運搬堆積作用
3A 河川での浸食運搬堆積作用
実際に河川の流域でどうなるかを上流側から順に考えてみます。
上流部では、一般には流速が速くて侵食作用が起こると考えられています。実際には洪水時の流速が速いときに堆積物は持って行かれ、 洪水が治まったときに堆積物がためられます。河原の石などはこのように、洪水後にして置いて行かれたものです。 河床の岩盤は硬く、水流だけで削られることはありません。流されてきた土砂などがこすれることによって岩盤が削られて、 侵食作用が起こっています。侵食は川底を下に削るように行われ(下方侵食)、断面がV型の谷(V字谷)を作ります。
山間部から平野への出口では、流速が遅くなりますから、堆積がおこります。 山からの出口付近から放射状に堆積物をためていき扇状地が作られます。 堆積物は土石流によってもたらされたものが多いようです。
中下流域のはんらん原では、河川が氾濫した時やそれが治まっていく時に堆積が起こります。 流れの幅が広くなるかあるいは水量が減る事によって、流速が低下するためです。このときに自然堤防が作られます。 自然堤防の外側は、洪水時に氾濫した水がたまって後背湿地を作ったり、堆積した土砂によって氾濫原が作られます。
河の流れをみると大きくうねるように流れていることがあります。 一般的には、川の曲がりがだんだん大きくなって蛇行ができ、 それが進んでくると三日月湖(河跡湖)が作られるといわれています。 蛇行や三日月湖のでき方についてはこちらで考察していますので確認してみてください。
河口付近では、海に流れ込むことによって、流速が低下しますので堆積が起こるようにみえます。 実際には海には干満があり、満潮時には海水が川をさかのぼっていきます。流速が低下するのは、 満ちてくる海水に川の流れが押し戻されようとするときです。河口からだいぶ陸地側に入ったところで起こります。 そこでは、川の水がたまり、外側に広がって流れていこうとします。そのため川はいくつも枝分かれをしながら流れて行きます。 このようにしてできたのが三角州です。
洪水が起こったときには、河口で海水と混ざり急速に流れが遅くことははありません。 海面上に川の流路のようなものができ、そこを泥水が流れていきます。 その流れの、側面や底面では海水との摩擦により流速が低下しますので、堆積が開始されます。 頻繁に洪水を起こす川では、海の中に堤防のようなものが延びていく事があります。
天井川についてはこちらで解説しています。
3A-2 縦断曲線と平衡河川
川の流れでは、流路に沿って河口からの距離と標高との関係を表して縦断曲線というものが書かれることがあります。 大井川の縦断曲線を描いてみました。地理院地図で断面図を表示させるため機能を使って河川に沿うデータを作りそれから作画しています。 途中から東俣沢経由で間ノ岳に接近する沢までのものでます。
図からわかるのは、流れ初めは急傾斜で、流れて行くにつれてだんだん緩くなっています。
このあたりでは流れが遅くなることによって運ばれてきた土砂がたまっているとみられます。
河口から100km(長島ダム)あたりから下流側では川の傾斜はほとんど一定になっています。
流れの速さは一定なので、普段は土砂をためたり運び去ったりということはなさそうです。
大井川の縦断曲線が将来どのようになるかを考えてみます。南アルプスで隆起運動の激しいところにありますが、 このような地殻変動がなかったと仮定してみます。 上流部の傾斜がきついところは次第に侵食作用を受けてひくなっていきます。これに伴って傾斜は緩くなっていくでしょう。 下流部では侵食も堆積も起こりませんから、傾斜は変わらないでしょう。 だとすると、河川の縦断曲線は河口から最上流部まで一定の(ゆるやかな)傾斜を持つ川に変わっていきます。 このような川を平衡河川といいます。
日本ではどこでも地殻変動が激しく、縦断曲線を変化させますから、平衡河川というのはありません。 大陸の地殻変動がほとんど起こっていないところを流れる大河は平衡河川になっているものが多いようです。
3B 海水による侵食・運搬・堆積
海水も基本的には水ですから、ユルストローム図に従って、粒子を運んでいきます。粒径の小さな粘土粒子はこの法則に従いません。 表面がマイナスイオンに帯電されていて、海水中の陽イオンと反応・結合して比較的大きな塊となり、堆積しやすくなります。
海水が河川と比べてもう一つ違うのは全体の流量が大きく、流れの中で乱れがないことにあります。 海流に乗ってしまえば、はっきりわかる目標物がない限り流されていることがわかりません。 海水の流れに乱れがないため海流の中に入ってしまえば、コップに入れた水と同じようなものです。 水中に含まれる粒子は底の方に沈んでいきます。ある程度海流が流れると、その本体の中には砂や泥といった粒子は含まれなくなります。 したがって、海流が起こす作用は、流速が変化する流れの縁でのみ起こることになります。
海流は流れの大きさに比べて、周囲が土砂と接してる場所はありません。粒子を供給する場所がなく、粒子を運ぶことはあまりありません。 粒子がもたらされるのは、洪水等で川から運ばれてきたものが、海流に混ざった場合に起こります。 このような粒子はいったん海底にたまり、運ばれやすい砂粒が流れに乗って運ばれ、海流の沿岸部や縁の流れの弱いところに置いていかれます。 入り江の砂浜や、砂州・砂嘴といったものが作られます。 ダム建設などにより河川からの砂の供給が少なくなった事により、全国の海岸部で砂浜や砂州が細っているといわれています。 たまっているようにみえる砂粒も、運べなくなって堆積したものではありません。 運ばれる途中のもののようです。新しい砂粒がやってこない限り、いつかはなくなってしまうでしょう。
※砂州と砂嘴の違いについて:湾をふさぐようにできたものが砂州、 陸地から離れるようにできたものが砂嘴とされますが、陸から離れていく砂浜を全て砂州という場合もあるようです。
海流のように、一定方向に決まった強さの流れがあったとします。 海底が平らであっても、わずかな凹凸をきっかけにして、海水は海底のすぐ上で波打つように流れます。 この流れに合わせるように、砂が波の形にたまっていきます。このようにしてできたのが漣痕です。 流れが深い場合、土手くらいの大きさのものも作られることがあります。砂堆(dune)と呼んでいます。 これらのものも、海流が粒子を運んでいく一つの方法とみることができます。
海岸付近では波が打ちつけてきます。水が動いたり止まったりを繰り返し、 それによって動かされた粒子が岩盤を削ることによって侵食作用が起こります。 海水の動きが最も激しいのは海面付近の高さで、少し深くなるだけで波は急激に弱くなっていきます。 そのため、海面の高さのところが一番よく削られていきます。それより高いところは崩落することによって海食崖が作られま。 崖の下部には海食洞や海食洞門ができることがあります。 また、海水面のわずかに下側に、陸地を削り残して海食台(波食台)が作られます。
3C 風による侵食・運搬・堆積
風の働きも、海流と似たような形で起こります。海水と違うのは、粒子の運び去られる大きさやその風速がことなるというくらいです。 砂漠地帯や海岸付近には、砂堆に相当する砂丘が作られますし、 その表面には漣痕に相当する風紋ができます。
強風によって絶えず砂吹き飛ばされる場所では、地面に半分顔を出している岩石の表面がスプーンでえぐったように削られ 「三稜石」とよばれる形になるようです。また、岩が地表面付近の高さのところだけ削られ、キノコ岩となります。 日本ではこのようにしてできたキノコ型の岩は少ないようです。
海岸などでは、どこでもだいたい同じくらいの大きさの砂粒がたまっているようです。ユルストローム図を見る限りは、 いろいろな大きさの砂粒がたまっているところがあって良さそうです。 実際に、礫でできている海岸(礫浜)では、波の激しいところの方が大きな礫がたまっています。 どうして、砂の場合はそうならないのかを考えてみることにします。
4A 砂粒の初動速度
水の流れの中で、砂粒がどれくらいの速さの水流で動き出すかを考えてみます。 ユルストローム図の初動曲線は、粒径が0.1mmより少し大きな粒のところで下に膨らんでいます。 これは、この大きさの粒子が最もゆっくりとした流速で動き出す事を示しています。 見方を変えれば、流速が徐々に上がっていった場合、この粒径の粒子が最も早く動き出す事でもあります。 本当にそうなのかを、理論的に考えてみます。
先に述べたように、粒子が摩擦で止まっていようとする力より、流水に押されて流される力の方が強くなれば、粒子は動き出します。 摩擦の大きさは、粒子の質量に比例します。質量は体積に比例しますので、粒径の3乗に比例することになります。 摩擦力を F 、粒径を d とおいたとき次のような関係式が作れます。ただし、比例することを表す記号を「 ∝ 」 とします。
F ∝ d3
水流から受ける力は少し複雑です。粒径が大きな時は、ニュートンが考えた式に従います。
水流から受ける力を R 、粒子にあたる流れの速さを v とおくと次のようになります。
R ∝ d2 × v2
ここで v に注目します。これくらいの大きさの粒子の場合、水流がそのままの勢いで粒子にあたるわけではありません。 川底では、直上の水は動かない物と接していますから、その流れの速さは0です。 川底から少しずつ離れるにつれて、流れは速くなっていきます。その速さは、川底からの距離に比例するようです。 粒子にあたる流れの速さは、その中心にあたっている速さと見ることができます。 従って、流れの速さを V とおくと、次の式が作れます。
v ∝ V × d
これを、水から受ける力の大きさを求める式に代入すると
R ∝ d2 × ( V × d )2
R ∝ d4 × V2
粒子が動き出すときの流速は R = F ですから
d4 × V2 ∝ d3
変形して
d × V2 = 一定
粒径と流速の2乗が反比例するという式が作られました。 このことは、大きな粒子では、粒径が大きくなるほど動き出す水流の速さが小さくなることを示しています。
※経験と合わないような感じがします。それはさらに大きな粒子では、水底による効果が小さくなるからです。 実際に、この計算結果のような効果が現れるのは1cmくらいの大きさ以下の粒子です。 これより大きな粒子では、大きくなるほど水底の影響が小さくなっていきますから、v=Vの関係に近づいていきます。 その結果、大きな粒子ほど動かし始めるのに必要な流速は大きくなるという関係が求められます。
今度は、小さな粒子を考えてみます。水流から受ける力はストークスの式に従いますから
R ∝ d × v
です。川底の影響を考慮して式を変形すると
R ∝ d × ( d × V )
R ∝ d2 × V
R = F より
d2 × V ∝ d3
V ∝ d
今度は、粒径と流速は比例するという式になりました。 つまり、小さな粒子では、粒径が小さくなるほど動き出すのに必要な水流の速さが小さくなるということを示しています。
普通ニュートンの式が使えるのが5mmより大きな粒子で、ストークスの式が使えるのは0.15mmより小さな粒子とされています。 この間の大きさでは、中間的な式となります。初動速度もそれに合わせて変化するようです。
計算式からわかるのは、ニュートンの式からストークスの式へと移り変わる粒径は、他の粒径に比べて動きにくいということです。 実際にその大きさがどれくらいで、その時の流速がどれくらいなのかを確かめた実験があります※。 そこに書かれているデータをもとに作ったのが下の図です。
2mm以下の大きさでは、1.5mmくらいの位置で上に膨らんでいます。 これは、1.5mm程度の大きさの粒子が最も動きだしにくい事を示しています。この大きさの粒度は(第一)安定粒度といいます。 これくらいのくらいの大きさの粒子は、その前後の大きさの粒子に比べて残されやすいといえます。
※参考文献:木村晴彦 堆積機構の基礎的研究(その3)1954年 地質学雑誌60巻705号
※ユルストローム図では、粒径0.3mm以下では初動曲線は左上がりの線となっています。 このグラフで左下がりの線と異なる結果になっているのは、粒子が1つかたくさんあるかとの違いによると思われます。
4B 砂粒の運動速度
今度は、砂粒の運動速度に注目してみることにします。前述の論文に、流速と粒径・運動速度との関係を調べた実験結果も書かれています。 そのデータを使って、グラフを作ってみました。
流速ごとに色を変えて示します。 青線・赤線・緑線は、順番に30cm/s、35cm/s、40cm/sの流水中で、粒子の運動速度(cm/s)がいくらなのかを表しています。
青線(流速30cm/s)をみると、1.5mm付近の粒度では運動速度が0となっています。 粒子は動かないことを示してます。これは、ユルストローム図では堆積曲線より下の領域に入ったことを示しています。 この粒度では、赤線(流速35cm/s)になるまでは運動速度もゆっくりしているようです。
ここで測定されている運動速度は、水底を滑るようにして進む粒子の速度です。 粒径が小さい場合や流速が速い場合は、水中を漂うように流されていく粒子が増えます。その場合は、流速と同じ速度で流されていくことになります。
4C 波打ち際での砂の動き
浜の波打ち際で砂粒がどのように動くかを考えてみます。砂粒は、波の動きによって動かされます。 まず、波によって水と砂粒がどう動くかを見ていきます。砂粒の大きさはそろっているものとします。 波が打ち寄せて一番高くまで登ってきた状態から考え始めてみます。
このあと、波は引いていきます。一部は、砂粒の間にしみこんでいくものがありますので、打ち寄せてきたときよりは量が少なくなるでしょう。 引いていく水は、浜の斜面を下って加速していきます。ある程度の速度になったら、それよりは速くならないでしょう。 この時、流速が砂粒の初動速度より大きくなれば、砂粒はいっしょに持って行かれることになります。 それほど長い時間水は流れていませんから、浜の砂を全部持っていくことはないでしょう。大半の砂は残ったままになります。
しばらくすると、次の波が打ち寄せてきます。この波と、斜面を下ってきた水がぶつかります。 下ってきた水は押しとどめられ、勢いが弱くなります。この時、運んできた砂粒の大半をそこに落としていくでしょう。 しだいに、下ってくる水は少なくなり、逆に押し寄せてくる波は強くなっていきます。そのうち、押し寄せてきた波が浜を上っていくようになります。
押し寄せてきた波の勢いが、砂粒を動かすのに十分な勢いを持っていない場合、引いていく水の流れにも砂粒を動かすほどの勢いはありませんから、 変化は起こりえません。波が砂粒を動かしていく場合に絞って考えます。
 波は、波打ち際や浜にたまった砂を動かし、運び上げていきます。水が段々高いところに上がっていくと、
勢いが弱くなり、そのうちに砂粒を運べない速度になります。そこで、砂粒はおいて行かれるでしょう。
波の後半にやってきた水も、同じように砂粒を運び上げていきますが、波のピーク時のものに比べて勢いが弱いので、
それほど高く上がらないうちに砂粒をおいていくことになります。こうしてみると、砂粒はある高さまでの浜にばらまかれることになります。
写真は、波で運ばれてたまった砂が作った模様です。
波は、波打ち際や浜にたまった砂を動かし、運び上げていきます。水が段々高いところに上がっていくと、
勢いが弱くなり、そのうちに砂粒を運べない速度になります。そこで、砂粒はおいて行かれるでしょう。
波の後半にやってきた水も、同じように砂粒を運び上げていきますが、波のピーク時のものに比べて勢いが弱いので、
それほど高く上がらないうちに砂粒をおいていくことになります。こうしてみると、砂粒はある高さまでの浜にばらまかれることになります。
写真は、波で運ばれてたまった砂が作った模様です。
浜を駆け上がる波を見ていると、どこでもだいたい同じくらいの速さで動いているように見えます。 砂粒が運べなくなる速さになる時は、どこでもだいたい一緒ですから、ほとんど同時に砂粒をおいていくでしょう。
この後、波は一番高いところまで駆け上がっていきます。それからは、同じ事の繰り返しとなります。 浜の高いところも低いところも、ほとんど同時に波が引き始めますから、砂を運び始めるのもほぼ同時に始まるでしょう。 波が引いていくときに浜の砂を持ち去って、押し寄せてくるときに砂を持ってくることを繰り返します。
それでは、浜の砂はどうなっていくのでしょうか。押し寄せてくるときは勢いが強く、引いていくときには弱くなりますから、 段々砂がたまっていくことになりそうです。ここで考えておかないといけないことは、浜は海に向かって傾いていることです。 海から打ち寄せてきた波は、この斜面を駆け上がって行くことになります。砂粒も高いところに押し上げないといけません。 そのためには、余分に砂に力を加えないといけません。その分、波にも勢いが必要です。 逆に引いていく水は、斜面を下っていきます。砂粒も転がり落ちやすくなっていますから、小さな力で動き始めます。 引いていくときは、押し寄せてくるときより小さな力で砂粒が動き始めます。
斜面の傾斜がきつくなると、砂粒を押し上げる力はたくさん要ります。水の勢いが同じだと、砂粒は動きにくくなります。 引いていくときに、砂粒が勝手に落ちていこうとする力は大きくなります。同じ水の勢いでも、砂粒はたくさん動こうとするでしょう。
浜の傾斜がきつくなると、運ばれてくる砂の量は少なくなり、持ち去られる砂の量は多くなっていきます。 その結果、全体として浜の砂は持ち去れられて、傾斜が段々と緩くなっていきます。 逆に、傾斜が緩いと、高いところに砂が運ばれてきて、傾斜がきつくなっていきます。 最終的には、波が引いてくるときに持ち去られる砂の量と、押し寄せてくるときにたまる砂の量とが同じになる傾斜で落ち着くでしょう。 砂粒を持ち上げる限界の高さのあたりは、砂粒がたまり傾斜が急になりそうです。 実際にはやってくる波が打ち上げる高さは不揃いです。先ほどの写真のように波ごとに場所が変わり、まんべんなくばらまかれることになります。 潮が満ちてくると、波はだんだんと高いところに上がってきて、その先で砂をためていきます。 満潮時の波があたる一番高いところあたりには段の様なものができます。
砂粒の大きさが不揃いだと、浜の傾斜はどうなるでしょうか。 だいたいの傾向で考えます。砂粒の大きさが違うと、止まる時や動き出す時の流れの速さが違ってきます。 斜面を下る流れの速さは一定です。傾斜が緩いほど遅くなります。ゆっくりの流れで動き出す砂粒は、傾斜が緩くても動き始めることができます。 たくさん運び去るのにもそれほど速い流れは必要がないでしょう。その分、浜の傾斜は緩くなります。
いろいろな大きさの粒が混じっていると、浜の傾斜はどうなるでしょう。 よく動く砂粒が、緩やかな斜面を作ったとします。この斜面では、安定粒度(動きにくい)の砂粒は、波が引いていくときに持ち去られることはありません。 次第に高いところに集まってきて、傾斜をきつくしていくでしょう。 浜の傾斜がきつい場合、よく動く砂粒は持ち去られることによって浜の傾斜を緩くしようとします。
しかし、ここには持ち去られる事ができる砂粒はすぐに運び去られ残っていません。持って行かれない以上、傾斜を変えることができないのです。
浜の傾斜がきつい場合、よく動く砂粒は持ち去られることによって浜の傾斜を緩くしようとします。
しかし、ここには持ち去られる事ができる砂粒はすぐに運び去られ残っていません。持って行かれない以上、傾斜を変えることができないのです。
動きやすい砂粒の一部は、波打ち際の高いところに漂着物が打ちつけられているように、安定粒度の砂粒がある場所より高いところにたまることができます。 写真からは、サンゴのかけらの様な形がいびつで水の抵抗が大きく、動かされやすくなっているため、高いところに集まっているようすがわかります。 これ以外のものの多くは、波打ち際近くや波のぶつかるところで、波の動きに合わせていったり来たりを繰り返すことになるでしょう。
1.5mm前後の大きさ(安定粒度)の砂粒は他の砂粒に比べると動かされにくくなっています。そのため砂浜を作る砂粒の主体となります。 それ以外の砂粒は、波の動きに合わせてゆれ動いているのを見かけます。
補足:浜に砂が多い理由について
波が打ち上がっていく速度を見ると歩くよりも遅いくらいにみえます。歩く速度は1m/s程ですから、30〜50cm/sといったところでしょうか。※ この速度で運ばれてくる粒子は砂粒という事になります。これよりも小さな粒は流されてたまることはせきませんし、大きな粒は運ばれてきません。 必然的に砂が多くなってきます。砂浜ができる主要因は波の速度にありそうです。
砂浜での斜面の傾斜の大きさは、安定粒度の砂粒が決定します。その時の水の流れは、安定粒度の砂粒が動かされ始める限界くらいの速さになります。 この速さでも、それ以外の粒度の砂粒はかなりの速さで動かされます。このことは、先ほどの砂粒の運動速度に関係したグラフを見てもわかりますし、 実際に波打ち際で砂粒の動きを見ていてもわかります。動きが速ければその分だけ摩耗がはげしくなります。 大きな粒は削られ、すぐに安定粒度になるでしょう。小さな粒は削られるとさらに小さくなって運び去られやすくなります。 安定粒度の砂粒はほとんど動かないので、削られて小さくなっていくということは少ないでしょう。 この結果、浜は安定粒度の粒がたくさん見られる様になります。
実際には、これ以外にも砂粒を多くする要因があります。岩石、特に火成岩をみると、構成している鉱物の大きさは2mm以下のものがほとんどです。 大きくても、1cmを越えることはほとんどありません。 岩石が風化して破壊されるとき、構成する鉱物どうしの境界から壊れて、鉱物同士がばらばらになっていくことが普通です。 このようにしてできた粒の大きさは、2mmより小さなものが主体となります。これは、砂粒の大きさに相当します。
つまり、元々たくさん作られるから、砂はたくさんあるといえます。 これが、波の作用によって集められやすくなっていることが、海岸で砂をたくさん見かける理由となっています。 川などで、たくさんできているはずの砂をあまり見かけないのは、レキ(石ころ)に比べ流されやすいため、少し速い流れでもすぐに運び去られてなくなっていくからです。
※波が打ちつける速さについて
波が浜に打ちつけるときのようすを見るとある程度近づいた時の勢いでそのまま浜にぶつかり乗り上げていくようにみえます。
海底が非常に浅いところまでやってくると、波の低いところは海底までの高さは少なくなってきます。 波を維持するためには、この部分を引き返していく海水の流れが必要になりますが、水量が少なくなること、海底との摩擦が大きくなることであまり速い流れは作れません。 このようになってくると、押し寄せてきた勢いそのまま進んで行くようです。
波が海岸に打ちつけるときに、引き返す流れが少なくなっていることは、浜では離岸流ができる事からも推察できます。
引き返す波が少なくなるための条件として、波高が関係してきます。高いとそれだけ低い部分が海底に接近しないようにするための水深は深くなります。 ところで、波の速さは水深に関係してきます。波高の大きな波は深いところの勢いそのままやってみますから、打ちつける波は速くなります。 運ばれてくる粒子も大きくなりますから、砂浜ではなくレキ浜が作られるます。
1.流速と粒径
地学の教科書には、河川の流域で侵食・運搬・堆積がどのような場合に起こるかを示すために右のような図が載せられています。 ユルストローム図と呼ばれる図です。

|
| ユルストローム図 ユルストローム図はよく見かけるのですが、出典元が見つけられていません。 この図はいくつかの文献にある図を参考にして描いたものです。 従って、境界線付近で粒子がどのような運動をするかということについては正しく表現されていません。 あくまでも、説明用の参考図としてみてください。 |
もう少し詳しく見ていきます。グラフの横軸は粒径(粒子の直径)、縦軸は流速(川の流れの速さ)を表しています。 例えば、直径1mmの粒子(砂粒)があったとします。この粒子が流速1cm/sの流れの中にあるとどうなるでしょうか。 粒径1mmと流速1cm/sの位置は、Cの領域にあります。 ここは堆積の領域にあるので、この粒は堆積することになります。
流速が100cm/sになると、Aの領域に入ってきます。ここは侵食の領域ですので、この流れの中では侵食されることなります。 流速が10cm/sでは、運搬されることになります。この図からは、粒子が運ばれていくのか、運ばれてきたものが堆積するのかを読み取ることができます。
この方法を逆に使ってみることにします。洪水があって治まった後に、川底に10cm(100mm)の石がたまっていたとします。 この大きさの粒子が運ばれるのは、BとCとの境界線より上です。粒径10cmの縦線を上にたどっていって、BCの境界線と交わるところの流速は100cm/sです。 このことから、洪水時の流速はこれよりも速かったことが読み取られます。
なお、図の縦軸・横軸とも目盛りのはばが10倍(別に何倍でもよいが)になる毎に等間隔だけずれていくというつけかたになっています。 このような形の目盛りがついたグラフを両対数グラフと言います。 非常に大きな数値と小さな数値が混ざっているときに便利なグラフです。
※侵食の「しん」の字は「浸」をあてることがあります。おもに水が関わっていますから、「さんずい」の方が適切なように思えます。 人が関わらないので「にんべん」を使うのは違和感がありますが、慣例に従って「侵食」を用いることにします。 「しょく」についても「蝕(むしばむ)」が正しい文字です。
なお、このサイト内の他のページでは、習慣で「浸食」を使っているところもあります。
2.ユルストローム図の実際の意味
この図がどういう意味を持っているのかもう少し詳しく見ていくことにします。
いま、川底に砂粒が一つあるとします。この上を川の水が流れると砂粒を押す力が働きます。ところが、砂粒と川底との間に摩擦力が働きますので、 砂粒は簡単に動きません。水流が早くなって、砂粒を押す力が大きくなり、砂粒の最大摩擦力より大きくなったときに砂粒が動き出します。 この時の流速を仮に「初動速度」と呼ぶことにします。
今度は、同じ大きさの砂粒が流されてきたとします。当然、形や密度は同じものとします。この場合も、川の流れが押す力よりも摩擦力の方が大きければ、 砂粒の動いている速さはだんだん遅くなって最後には止まってしまいます。川の流れがある速度より小さくなると、砂粒が止まることになります。 砂粒がいっぱいやってくれば、この速度以下では堆積が起こるということで、これも仮に「堆積速度」と呼ぶことにします。
初動速度と堆積速度を比べてみます。摩擦力は動き出すときが最大になりますから、その分だけ動かすためには大きな力が必要になります。 したがって、堆積速度より初動速度が大きくなります。横軸に粒径、縦軸に流速をとったグラフに表してみると、初動速度の方が上になります。 いろいろな粒径で、初動速度と堆積速度を表す点が取れます。これを結ぶと初動速度、堆積速度を表す線が引けます。 初動速度を表す線は「初動曲線」、堆積速度を表す線を「堆積曲線」と呼ぶことにします。当然、初動曲線は堆積曲線より上に引かれます。
| 仮に名付けた用語の出典元が見当たらなくなっていますが、このまま使うことにします。 「堆積曲線」は地層がどれくらいの速さでたまっていったかを示すグラフに用いられています。 この用語は使わない方がいいのかも知れません。 | |
| ※2 | 粒子を押す力は粒子の形や密度にも影響されます。また、摩擦の大きさは底面の状態によって変わってきます。 そのため、実際にはグラフはある程度の幅を持った線で引かれることになります。そのように書かれている図を見かけることもあります。 |
| ※3 | 水中で粒子を押す力を支配する物理法則が粒径によって変わるため、粒径1mm付近でグラフの傾きが変わります。 |
| ※4 | 粒子が小さくなると粒子間のすき間が小さくなります。狭いすき間に入りこんだ水は、粘性の影響が大きくなり、 動きにくくなっていきます。その結果、水は粒子どうしをくっつけるように働き、大きな粒子がある場合のように粒子を動かし始めにくくなります。 たくさんの小さな粒子が積み重なっている場合、初動曲線は左上がりの線になります。 |
今度は、それぞれの領域が何を示しているかを考えてみます。図を再提示します。
 まず、Aの領域です。いま流速100cm/sの流れの水路で、粒径1mmの砂粒があったとします。
川底に止まっていたとしても、この領域に入る流速なら流されていきます。結局、この大きさの粒子は全てなくなってしまいます。
粒子が全てなくなるまでは運び去られます。言いかえれば、侵食されるといえます。しかし、流れは過去からずっとあったはずです。
とすると、流される粒子はとうの昔に運び去られ、なくなってしまっていると考えた方が妥当です。
つまり、侵食されるべき粒子はないので、侵食は起こらないことになります。
結局、Aの領域は侵食の領域ではないといえます。もっとも砂粒は流され続けていますから、運搬の領域であることはまちがいありません。
まず、Aの領域です。いま流速100cm/sの流れの水路で、粒径1mmの砂粒があったとします。
川底に止まっていたとしても、この領域に入る流速なら流されていきます。結局、この大きさの粒子は全てなくなってしまいます。
粒子が全てなくなるまでは運び去られます。言いかえれば、侵食されるといえます。しかし、流れは過去からずっとあったはずです。
とすると、流される粒子はとうの昔に運び去られ、なくなってしまっていると考えた方が妥当です。
つまり、侵食されるべき粒子はないので、侵食は起こらないことになります。
結局、Aの領域は侵食の領域ではないといえます。もっとも砂粒は流され続けていますから、運搬の領域であることはまちがいありません。同様にBの領域を考えます。止まっていた粒はABの境界を越える速さではないので、動き出すことはできません。 止まったままです。逆に動いている粒は、BCの境界線を下回りませんので、止まらず動いたままです。 つまり、この領域には、同じ大きさの粒でも動いているものと止まっているものとがあることになります。
最後にCの領域です。動いていたものも止まります。堆積していくように見えますが、この流速では粒子を運ぶことはできません。 定常的な流れがあったとすると、粒子はとっくの昔に止まってしまっていて、運ばれてくることはありません。 したがって、たまるものがやってこない以上堆積は起こりえません。 この領域は、堆積の起こる場所ではなく、該当するすべての粒子が動かない領域になります。
まとめてみます。ユルストローム図の、ABCの各領域は、侵食・運搬・堆積ではなく次の状態を表していることになります。
Aの領域−−該当する全ての粒子は動いている
Bの領域−−該当する粒子は、動いているものと止まっているものがある
Cの領域−−該当する全ての粒子は止まっている
図の中で大きな意味を持っているのは、それぞれの境界線で、
ABの境界線−−止まっていた粒子が動き出す境界(初動曲線)
BCの境界線−−動いていた粒子が止まり出す境界(堆積曲線)
を表しています。
3.侵食・堆積の起こる場所
ここまでの説明では、侵食・運搬・堆積の起こる場所が図に記入されていない様に思えます。 工夫すると堆積や侵食の起こる場所も読み取ることができます。各境界線の説明を見直してみることにします。
堆積の起こる場所を考えてみます。動いていた粒子が止まるということは、堆積が起こった事を示しています。 BCの境界線はまさにそのような場所です。この線より上では、動いている粒子があります。逆に下では全ての粒子が止まっています。 この線を上から下方向に横断するように流速が変化したときに動いている粒子が止まり、その粒子が堆積します。 簡単に言えば、BC線(堆積曲線)をまたいで流速が遅くなるときに堆積が起こることになります。 1mmの粒子は流速が約6cm/sを切るようになったときに堆積します。
同様に、侵食の起こる場所はABの境界線(初動曲線)をまたいで流速が速くなるところになります。 1mmの粒子は流速が約30cm/sを越えるようになったときに運び去られ(=侵食し)始めます。
| ※ |
ここでは流水の運搬量については考慮していません。運搬限界量以下の場合を想定しています。 初動曲線付近の流速では、粒子が運ばれていくときは、水底を滑るように流されていきます。 この時、粒子の分布密度が大きくなると、流水が粒子を押す勢いをつけられなくなります。 そのため、粒子の分布密度にも限界があります。 流れの幅が一定な場合、流速が速くなると、粒子の運動速度も速くなり、粒子の移動距離も長くなります。 同じ密度で粒子が通過したとしても、一定時間に通過する粒子の数は増えます。運搬可能な量は多くなります。 したがって、流水が運搬限界量に達している場合、流速が遅くなると、限界量が少なくなった分だけ粒子を落としていくことが考えられます。 つまり、ユルストローム図のAやBの領域であっても、流速の減少によって堆積が起こる場合が考えられます。 もちろん、Bの領域では流速の増大によって侵食が始まるということはありません。 |
 3A 河川での浸食運搬堆積作用
3A 河川での浸食運搬堆積作用実際に河川の流域でどうなるかを上流側から順に考えてみます。
上流部では、一般には流速が速くて侵食作用が起こると考えられています。実際には洪水時の流速が速いときに堆積物は持って行かれ、 洪水が治まったときに堆積物がためられます。河原の石などはこのように、洪水後にして置いて行かれたものです。 河床の岩盤は硬く、水流だけで削られることはありません。流されてきた土砂などがこすれることによって岩盤が削られて、 侵食作用が起こっています。侵食は川底を下に削るように行われ(下方侵食)、断面がV型の谷(V字谷)を作ります。
山間部から平野への出口では、流速が遅くなりますから、堆積がおこります。 山からの出口付近から放射状に堆積物をためていき扇状地が作られます。 堆積物は土石流によってもたらされたものが多いようです。
中下流域のはんらん原では、河川が氾濫した時やそれが治まっていく時に堆積が起こります。 流れの幅が広くなるかあるいは水量が減る事によって、流速が低下するためです。このときに自然堤防が作られます。 自然堤防の外側は、洪水時に氾濫した水がたまって後背湿地を作ったり、堆積した土砂によって氾濫原が作られます。
河の流れをみると大きくうねるように流れていることがあります。 一般的には、川の曲がりがだんだん大きくなって蛇行ができ、 それが進んでくると三日月湖(河跡湖)が作られるといわれています。 蛇行や三日月湖のでき方についてはこちらで考察していますので確認してみてください。
河口付近では、海に流れ込むことによって、流速が低下しますので堆積が起こるようにみえます。 実際には海には干満があり、満潮時には海水が川をさかのぼっていきます。流速が低下するのは、 満ちてくる海水に川の流れが押し戻されようとするときです。河口からだいぶ陸地側に入ったところで起こります。 そこでは、川の水がたまり、外側に広がって流れていこうとします。そのため川はいくつも枝分かれをしながら流れて行きます。 このようにしてできたのが三角州です。
洪水が起こったときには、河口で海水と混ざり急速に流れが遅くことははありません。 海面上に川の流路のようなものができ、そこを泥水が流れていきます。 その流れの、側面や底面では海水との摩擦により流速が低下しますので、堆積が開始されます。 頻繁に洪水を起こす川では、海の中に堤防のようなものが延びていく事があります。
天井川についてはこちらで解説しています。
3A-2 縦断曲線と平衡河川
川の流れでは、流路に沿って河口からの距離と標高との関係を表して縦断曲線というものが書かれることがあります。 大井川の縦断曲線を描いてみました。地理院地図で断面図を表示させるため機能を使って河川に沿うデータを作りそれから作画しています。 途中から東俣沢経由で間ノ岳に接近する沢までのものでます。
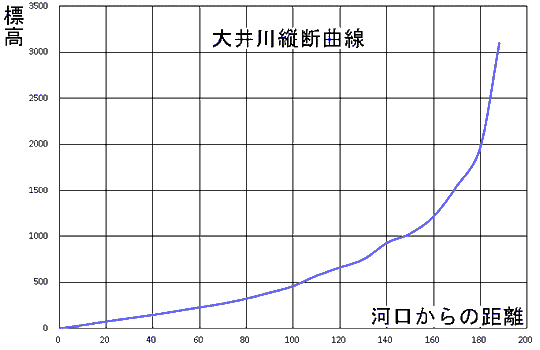
|
| 図 大井川縦断曲線 |
大井川の縦断曲線が将来どのようになるかを考えてみます。南アルプスで隆起運動の激しいところにありますが、 このような地殻変動がなかったと仮定してみます。 上流部の傾斜がきついところは次第に侵食作用を受けてひくなっていきます。これに伴って傾斜は緩くなっていくでしょう。 下流部では侵食も堆積も起こりませんから、傾斜は変わらないでしょう。 だとすると、河川の縦断曲線は河口から最上流部まで一定の(ゆるやかな)傾斜を持つ川に変わっていきます。 このような川を平衡河川といいます。
日本ではどこでも地殻変動が激しく、縦断曲線を変化させますから、平衡河川というのはありません。 大陸の地殻変動がほとんど起こっていないところを流れる大河は平衡河川になっているものが多いようです。
この項 2024/06/30 作成
3B 海水による侵食・運搬・堆積
海水も基本的には水ですから、ユルストローム図に従って、粒子を運んでいきます。粒径の小さな粘土粒子はこの法則に従いません。 表面がマイナスイオンに帯電されていて、海水中の陽イオンと反応・結合して比較的大きな塊となり、堆積しやすくなります。
海水が河川と比べてもう一つ違うのは全体の流量が大きく、流れの中で乱れがないことにあります。 海流に乗ってしまえば、はっきりわかる目標物がない限り流されていることがわかりません。 海水の流れに乱れがないため海流の中に入ってしまえば、コップに入れた水と同じようなものです。 水中に含まれる粒子は底の方に沈んでいきます。ある程度海流が流れると、その本体の中には砂や泥といった粒子は含まれなくなります。 したがって、海流が起こす作用は、流速が変化する流れの縁でのみ起こることになります。
海流は流れの大きさに比べて、周囲が土砂と接してる場所はありません。粒子を供給する場所がなく、粒子を運ぶことはあまりありません。 粒子がもたらされるのは、洪水等で川から運ばれてきたものが、海流に混ざった場合に起こります。 このような粒子はいったん海底にたまり、運ばれやすい砂粒が流れに乗って運ばれ、海流の沿岸部や縁の流れの弱いところに置いていかれます。 入り江の砂浜や、砂州・砂嘴といったものが作られます。 ダム建設などにより河川からの砂の供給が少なくなった事により、全国の海岸部で砂浜や砂州が細っているといわれています。 たまっているようにみえる砂粒も、運べなくなって堆積したものではありません。 運ばれる途中のもののようです。新しい砂粒がやってこない限り、いつかはなくなってしまうでしょう。
※砂州と砂嘴の違いについて:湾をふさぐようにできたものが砂州、 陸地から離れるようにできたものが砂嘴とされますが、陸から離れていく砂浜を全て砂州という場合もあるようです。
海流のように、一定方向に決まった強さの流れがあったとします。 海底が平らであっても、わずかな凹凸をきっかけにして、海水は海底のすぐ上で波打つように流れます。 この流れに合わせるように、砂が波の形にたまっていきます。このようにしてできたのが漣痕です。 流れが深い場合、土手くらいの大きさのものも作られることがあります。砂堆(dune)と呼んでいます。 これらのものも、海流が粒子を運んでいく一つの方法とみることができます。
海岸付近では波が打ちつけてきます。水が動いたり止まったりを繰り返し、 それによって動かされた粒子が岩盤を削ることによって侵食作用が起こります。 海水の動きが最も激しいのは海面付近の高さで、少し深くなるだけで波は急激に弱くなっていきます。 そのため、海面の高さのところが一番よく削られていきます。それより高いところは崩落することによって海食崖が作られま。 崖の下部には海食洞や海食洞門ができることがあります。 また、海水面のわずかに下側に、陸地を削り残して海食台(波食台)が作られます。
3C 風による侵食・運搬・堆積
風の働きも、海流と似たような形で起こります。海水と違うのは、粒子の運び去られる大きさやその風速がことなるというくらいです。 砂漠地帯や海岸付近には、砂堆に相当する砂丘が作られますし、 その表面には漣痕に相当する風紋ができます。
強風によって絶えず砂吹き飛ばされる場所では、地面に半分顔を出している岩石の表面がスプーンでえぐったように削られ 「三稜石」とよばれる形になるようです。また、岩が地表面付近の高さのところだけ削られ、キノコ岩となります。 日本ではこのようにしてできたキノコ型の岩は少ないようです。
2014/04/06 掲載
4.砂粒の運動海岸などでは、どこでもだいたい同じくらいの大きさの砂粒がたまっているようです。ユルストローム図を見る限りは、 いろいろな大きさの砂粒がたまっているところがあって良さそうです。 実際に、礫でできている海岸(礫浜)では、波の激しいところの方が大きな礫がたまっています。 どうして、砂の場合はそうならないのかを考えてみることにします。
4A 砂粒の初動速度
水の流れの中で、砂粒がどれくらいの速さの水流で動き出すかを考えてみます。 ユルストローム図の初動曲線は、粒径が0.1mmより少し大きな粒のところで下に膨らんでいます。 これは、この大きさの粒子が最もゆっくりとした流速で動き出す事を示しています。 見方を変えれば、流速が徐々に上がっていった場合、この粒径の粒子が最も早く動き出す事でもあります。 本当にそうなのかを、理論的に考えてみます。
先に述べたように、粒子が摩擦で止まっていようとする力より、流水に押されて流される力の方が強くなれば、粒子は動き出します。 摩擦の大きさは、粒子の質量に比例します。質量は体積に比例しますので、粒径の3乗に比例することになります。 摩擦力を F 、粒径を d とおいたとき次のような関係式が作れます。ただし、比例することを表す記号を
F ∝ d3
水流から受ける力は少し複雑です。粒径が大きな時は、ニュートンが考えた式に従います。
水流から受ける力を R 、粒子にあたる流れの速さを v とおくと次のようになります。
R ∝ d2 × v2
ここで v に注目します。これくらいの大きさの粒子の場合、水流がそのままの勢いで粒子にあたるわけではありません。 川底では、直上の水は動かない物と接していますから、その流れの速さは0です。 川底から少しずつ離れるにつれて、流れは速くなっていきます。その速さは、川底からの距離に比例するようです。 粒子にあたる流れの速さは、その中心にあたっている速さと見ることができます。 従って、流れの速さを V とおくと、次の式が作れます。
v ∝ V × d
これを、水から受ける力の大きさを求める式に代入すると
R ∝ d2 × ( V × d )2
R ∝ d4 × V2
粒子が動き出すときの流速は R = F ですから
d4 × V2 ∝ d3
変形して
d × V2 = 一定
粒径と流速の2乗が反比例するという式が作られました。 このことは、大きな粒子では、粒径が大きくなるほど動き出す水流の速さが小さくなることを示しています。
※経験と合わないような感じがします。それはさらに大きな粒子では、水底による効果が小さくなるからです。 実際に、この計算結果のような効果が現れるのは1cmくらいの大きさ以下の粒子です。 これより大きな粒子では、大きくなるほど水底の影響が小さくなっていきますから、v=Vの関係に近づいていきます。 その結果、大きな粒子ほど動かし始めるのに必要な流速は大きくなるという関係が求められます。
今度は、小さな粒子を考えてみます。水流から受ける力はストークスの式に従いますから
R ∝ d × v
です。川底の影響を考慮して式を変形すると
R ∝ d × ( d × V )
R ∝ d2 × V
R = F より
d2 × V ∝ d3
V ∝ d
今度は、粒径と流速は比例するという式になりました。 つまり、小さな粒子では、粒径が小さくなるほど動き出すのに必要な水流の速さが小さくなるということを示しています。
普通ニュートンの式が使えるのが5mmより大きな粒子で、ストークスの式が使えるのは0.15mmより小さな粒子とされています。 この間の大きさでは、中間的な式となります。初動速度もそれに合わせて変化するようです。
計算式からわかるのは、ニュートンの式からストークスの式へと移り変わる粒径は、他の粒径に比べて動きにくいということです。 実際にその大きさがどれくらいで、その時の流速がどれくらいなのかを確かめた実験があります※。 そこに書かれているデータをもとに作ったのが下の図です。
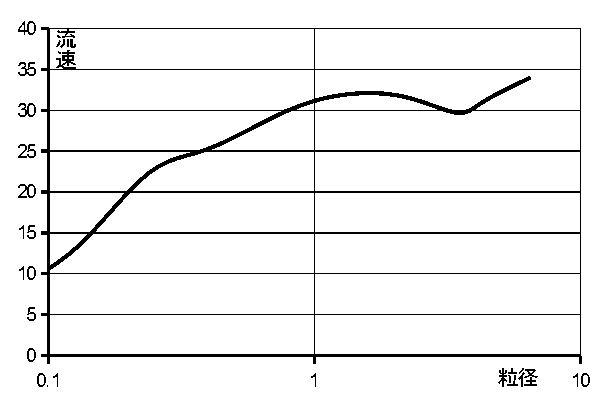
|
| 図 粒径と初動速度との関係 |
2mm以下の大きさでは、1.5mmくらいの位置で上に膨らんでいます。 これは、1.5mm程度の大きさの粒子が最も動きだしにくい事を示しています。この大きさの粒度は(第一)安定粒度といいます。 これくらいのくらいの大きさの粒子は、その前後の大きさの粒子に比べて残されやすいといえます。
※参考文献:木村晴彦 堆積機構の基礎的研究(その3)1954年 地質学雑誌60巻705号
※ユルストローム図では、粒径0.3mm以下では初動曲線は左上がりの線となっています。 このグラフで左下がりの線と異なる結果になっているのは、粒子が1つかたくさんあるかとの違いによると思われます。
4B 砂粒の運動速度
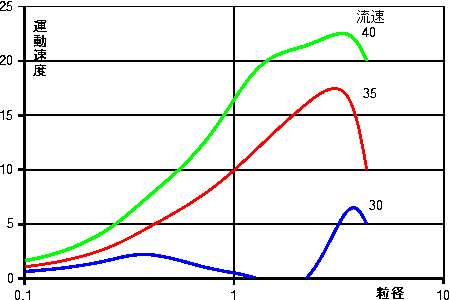
今度は、砂粒の運動速度に注目してみることにします。前述の論文に、流速と粒径・運動速度との関係を調べた実験結果も書かれています。 そのデータを使って、グラフを作ってみました。
|
| 図 粒径と運動速度との関係 |
流速ごとに色を変えて示します。 青線・赤線・緑線は、順番に30cm/s、35cm/s、40cm/sの流水中で、粒子の運動速度(cm/s)がいくらなのかを表しています。
青線(流速30cm/s)をみると、1.5mm付近の粒度では運動速度が0となっています。 粒子は動かないことを示してます。これは、ユルストローム図では堆積曲線より下の領域に入ったことを示しています。 この粒度では、赤線(流速35cm/s)になるまでは運動速度もゆっくりしているようです。
ここで測定されている運動速度は、水底を滑るようにして進む粒子の速度です。 粒径が小さい場合や流速が速い場合は、水中を漂うように流されていく粒子が増えます。その場合は、流速と同じ速度で流されていくことになります。
4C 波打ち際での砂の動き
浜の波打ち際で砂粒がどのように動くかを考えてみます。砂粒は、波の動きによって動かされます。 まず、波によって水と砂粒がどう動くかを見ていきます。砂粒の大きさはそろっているものとします。 波が打ち寄せて一番高くまで登ってきた状態から考え始めてみます。
このあと、波は引いていきます。一部は、砂粒の間にしみこんでいくものがありますので、打ち寄せてきたときよりは量が少なくなるでしょう。 引いていく水は、浜の斜面を下って加速していきます。ある程度の速度になったら、それよりは速くならないでしょう。 この時、流速が砂粒の初動速度より大きくなれば、砂粒はいっしょに持って行かれることになります。 それほど長い時間水は流れていませんから、浜の砂を全部持っていくことはないでしょう。大半の砂は残ったままになります。
しばらくすると、次の波が打ち寄せてきます。この波と、斜面を下ってきた水がぶつかります。 下ってきた水は押しとどめられ、勢いが弱くなります。この時、運んできた砂粒の大半をそこに落としていくでしょう。 しだいに、下ってくる水は少なくなり、逆に押し寄せてくる波は強くなっていきます。そのうち、押し寄せてきた波が浜を上っていくようになります。
押し寄せてきた波の勢いが、砂粒を動かすのに十分な勢いを持っていない場合、引いていく水の流れにも砂粒を動かすほどの勢いはありませんから、 変化は起こりえません。波が砂粒を動かしていく場合に絞って考えます。
 波は、波打ち際や浜にたまった砂を動かし、運び上げていきます。水が段々高いところに上がっていくと、
勢いが弱くなり、そのうちに砂粒を運べない速度になります。そこで、砂粒はおいて行かれるでしょう。
波の後半にやってきた水も、同じように砂粒を運び上げていきますが、波のピーク時のものに比べて勢いが弱いので、
それほど高く上がらないうちに砂粒をおいていくことになります。こうしてみると、砂粒はある高さまでの浜にばらまかれることになります。
写真は、波で運ばれてたまった砂が作った模様です。
波は、波打ち際や浜にたまった砂を動かし、運び上げていきます。水が段々高いところに上がっていくと、
勢いが弱くなり、そのうちに砂粒を運べない速度になります。そこで、砂粒はおいて行かれるでしょう。
波の後半にやってきた水も、同じように砂粒を運び上げていきますが、波のピーク時のものに比べて勢いが弱いので、
それほど高く上がらないうちに砂粒をおいていくことになります。こうしてみると、砂粒はある高さまでの浜にばらまかれることになります。
写真は、波で運ばれてたまった砂が作った模様です。浜を駆け上がる波を見ていると、どこでもだいたい同じくらいの速さで動いているように見えます。 砂粒が運べなくなる速さになる時は、どこでもだいたい一緒ですから、ほとんど同時に砂粒をおいていくでしょう。
この後、波は一番高いところまで駆け上がっていきます。それからは、同じ事の繰り返しとなります。 浜の高いところも低いところも、ほとんど同時に波が引き始めますから、砂を運び始めるのもほぼ同時に始まるでしょう。 波が引いていくときに浜の砂を持ち去って、押し寄せてくるときに砂を持ってくることを繰り返します。
それでは、浜の砂はどうなっていくのでしょうか。押し寄せてくるときは勢いが強く、引いていくときには弱くなりますから、 段々砂がたまっていくことになりそうです。ここで考えておかないといけないことは、浜は海に向かって傾いていることです。 海から打ち寄せてきた波は、この斜面を駆け上がって行くことになります。砂粒も高いところに押し上げないといけません。 そのためには、余分に砂に力を加えないといけません。その分、波にも勢いが必要です。 逆に引いていく水は、斜面を下っていきます。砂粒も転がり落ちやすくなっていますから、小さな力で動き始めます。 引いていくときは、押し寄せてくるときより小さな力で砂粒が動き始めます。
斜面の傾斜がきつくなると、砂粒を押し上げる力はたくさん要ります。水の勢いが同じだと、砂粒は動きにくくなります。 引いていくときに、砂粒が勝手に落ちていこうとする力は大きくなります。同じ水の勢いでも、砂粒はたくさん動こうとするでしょう。
浜の傾斜がきつくなると、運ばれてくる砂の量は少なくなり、持ち去られる砂の量は多くなっていきます。 その結果、全体として浜の砂は持ち去れられて、傾斜が段々と緩くなっていきます。 逆に、傾斜が緩いと、高いところに砂が運ばれてきて、傾斜がきつくなっていきます。 最終的には、波が引いてくるときに持ち去られる砂の量と、押し寄せてくるときにたまる砂の量とが同じになる傾斜で落ち着くでしょう。 砂粒を持ち上げる限界の高さのあたりは、砂粒がたまり傾斜が急になりそうです。 実際にはやってくる波が打ち上げる高さは不揃いです。先ほどの写真のように波ごとに場所が変わり、まんべんなくばらまかれることになります。 潮が満ちてくると、波はだんだんと高いところに上がってきて、その先で砂をためていきます。 満潮時の波があたる一番高いところあたりには段の様なものができます。
砂粒の大きさが不揃いだと、浜の傾斜はどうなるでしょうか。 だいたいの傾向で考えます。砂粒の大きさが違うと、止まる時や動き出す時の流れの速さが違ってきます。 斜面を下る流れの速さは一定です。傾斜が緩いほど遅くなります。ゆっくりの流れで動き出す砂粒は、傾斜が緩くても動き始めることができます。 たくさん運び去るのにもそれほど速い流れは必要がないでしょう。その分、浜の傾斜は緩くなります。
いろいろな大きさの粒が混じっていると、浜の傾斜はどうなるでしょう。 よく動く砂粒が、緩やかな斜面を作ったとします。この斜面では、安定粒度(動きにくい)の砂粒は、波が引いていくときに持ち去られることはありません。 次第に高いところに集まってきて、傾斜をきつくしていくでしょう。
 浜の傾斜がきつい場合、よく動く砂粒は持ち去られることによって浜の傾斜を緩くしようとします。
しかし、ここには持ち去られる事ができる砂粒はすぐに運び去られ残っていません。持って行かれない以上、傾斜を変えることができないのです。
浜の傾斜がきつい場合、よく動く砂粒は持ち去られることによって浜の傾斜を緩くしようとします。
しかし、ここには持ち去られる事ができる砂粒はすぐに運び去られ残っていません。持って行かれない以上、傾斜を変えることができないのです。動きやすい砂粒の一部は、波打ち際の高いところに漂着物が打ちつけられているように、安定粒度の砂粒がある場所より高いところにたまることができます。 写真からは、サンゴのかけらの様な形がいびつで水の抵抗が大きく、動かされやすくなっているため、高いところに集まっているようすがわかります。 これ以外のものの多くは、波打ち際近くや波のぶつかるところで、波の動きに合わせていったり来たりを繰り返すことになるでしょう。
1.5mm前後の大きさ(安定粒度)の砂粒は他の砂粒に比べると動かされにくくなっています。そのため砂浜を作る砂粒の主体となります。 それ以外の砂粒は、波の動きに合わせてゆれ動いているのを見かけます。
補足:浜に砂が多い理由について
波が打ち上がっていく速度を見ると歩くよりも遅いくらいにみえます。歩く速度は1m/s程ですから、30〜50cm/sといったところでしょうか。※ この速度で運ばれてくる粒子は砂粒という事になります。これよりも小さな粒は流されてたまることはせきませんし、大きな粒は運ばれてきません。 必然的に砂が多くなってきます。砂浜ができる主要因は波の速度にありそうです。
砂浜での斜面の傾斜の大きさは、安定粒度の砂粒が決定します。その時の水の流れは、安定粒度の砂粒が動かされ始める限界くらいの速さになります。 この速さでも、それ以外の粒度の砂粒はかなりの速さで動かされます。このことは、先ほどの砂粒の運動速度に関係したグラフを見てもわかりますし、 実際に波打ち際で砂粒の動きを見ていてもわかります。動きが速ければその分だけ摩耗がはげしくなります。 大きな粒は削られ、すぐに安定粒度になるでしょう。小さな粒は削られるとさらに小さくなって運び去られやすくなります。 安定粒度の砂粒はほとんど動かないので、削られて小さくなっていくということは少ないでしょう。 この結果、浜は安定粒度の粒がたくさん見られる様になります。
実際には、これ以外にも砂粒を多くする要因があります。岩石、特に火成岩をみると、構成している鉱物の大きさは2mm以下のものがほとんどです。 大きくても、1cmを越えることはほとんどありません。 岩石が風化して破壊されるとき、構成する鉱物どうしの境界から壊れて、鉱物同士がばらばらになっていくことが普通です。 このようにしてできた粒の大きさは、2mmより小さなものが主体となります。これは、砂粒の大きさに相当します。
つまり、元々たくさん作られるから、砂はたくさんあるといえます。 これが、波の作用によって集められやすくなっていることが、海岸で砂をたくさん見かける理由となっています。 川などで、たくさんできているはずの砂をあまり見かけないのは、レキ(石ころ)に比べ流されやすいため、少し速い流れでもすぐに運び去られてなくなっていくからです。
※波が打ちつける速さについて
波が浜に打ちつけるときのようすを見るとある程度近づいた時の勢いでそのまま浜にぶつかり乗り上げていくようにみえます。
海底が非常に浅いところまでやってくると、波の低いところは海底までの高さは少なくなってきます。 波を維持するためには、この部分を引き返していく海水の流れが必要になりますが、水量が少なくなること、海底との摩擦が大きくなることであまり速い流れは作れません。 このようになってくると、押し寄せてきた勢いそのまま進んで行くようです。
波が海岸に打ちつけるときに、引き返す流れが少なくなっていることは、浜では離岸流ができる事からも推察できます。
引き返す波が少なくなるための条件として、波高が関係してきます。高いとそれだけ低い部分が海底に接近しないようにするための水深は深くなります。 ところで、波の速さは水深に関係してきます。波高の大きな波は深いところの勢いそのままやってみますから、打ちつける波は速くなります。 運ばれてくる粒子も大きくなりますから、砂浜ではなくレキ浜が作られるます。
この節2017/04/21 作成
2024/06/xx 加筆
2014/04/06 ページ作成
2017/04/21 一部 修正
2024/06/xx 3A2追加
2017/04/21 一部 修正
2024/06/xx 3A2追加
<ヨッシンと地学の散歩>
<<一つ前 次へ >>